UNR #9

笔试

Day 1

官方题解

T1

考虑从后往前推，删点。

显然只有第偶数步肯能 \(s_i=0\)，只考虑第偶数步，每次删 \(2\) 个点。

考虑 \(\mathrm C\) 性质：

先找到最重边 \((p,q)\)（切断后 \(|siz_p-siz_q|\) 最小的边），然后可能 \((p,q)\) 挂在一条链上。

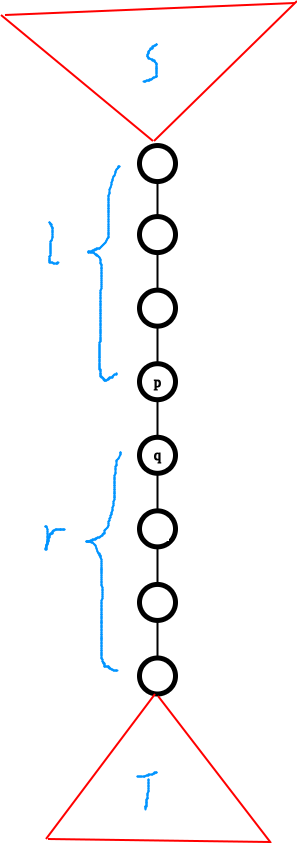
由于 \(s_n=0\)，\(S+l=T+r\)。

不妨设 \(l<r\)，那么 \(T\) 里面每删 \(2\) 个点，重边就会往 \(S\) 方向挪一步。

所以后 \(l+1\) 步 都必须是 \(0\)。

之后 \(p\) 怼在 \(S\) 上，重边不可能再挪。

• \(s_i=1\) ，若已经不平衡，\(S,T\) 各删除一点，否则删两个 \(T\) 内的点。
• \(s_i=0\) ，若已经平衡，\(S,T\) 各删除一点，否则删两个 \(S\) 内的点。

容易发现 \(S\) 这一侧点数始终不超过 \(T\) 这一侧的，然而 \(S\) 这一侧挪不动了，所以是合法的。

注意，删点按深度从大往小删，每次删最深的叶子。

用堆维护，\(O(n\log n)\)。改桶就 \(O(n)\)，懒得写。

接下来考虑 \(n\) 是偶数，\(s_n=1\) 的情况。

同样找到最重边 \((p,q)\)，若 \(siz_p=siz_q\) 就寄了。

显然后 \(\dfrac{|siz_p-siz_q|}{2}-1\) 步都必须是 \(0\)。

发现 \(p,q\) 往其中一侧偏了 \(2\) 个点，是上面构造过程的情况。

但是有可能 \(p,q\) 还在一条链上，用不了上面的构造。

实际上不会出现这种情况，若一开始 \(p,q\) 在一条链上，且 \(siz_p\ne siz_q\)，那么 \(siz_p,siz_q\) 之间最少差了 \(2\)，往旁边挪动肯定能更优。

所以可以延续上面的构造。

考虑 \(n\) 是奇数，只需删一个点即可。

先找到最重边 \((p,q)\)，再从 \(p\) 或 \(q\) 子树内删一个点，不妨设 \(siz_p<siz_q\)。

• \(siz_p+1=siz_q\)，若 \(s_n=0\) 则从 \(q\) 子树内删，否则从 \(p\) 子树内删。
• \(siz_p+1<siz_q\)，从 \(q\) 子树内删。

这里删点同样遵循上面的删点原则。

注意：最重边可能有两条，要做两遍。（赛时因为这个挂了 \(50\)）

AC Record

---

T2

先把 \(a\) 和 \(b\) 放在一起排序，排出来 \(a,b\) 间隔的序列。

例如：\(\red a\red a\blue b\red a\blue b\blue b\red a\blue b\)。

将 \(a\) 视为 \(+1\)，\(b\) 视为 \(-1\)，画出折线图：

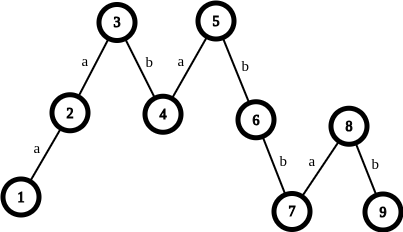
结论：匹配时必定是同一层的 \(\red a\) 和 \(\blue b\) 匹配，可以调整法证明。

每层显然是相邻的 \(\red a\) 和 \(\blue b\) 匹配，记这一层的点有 \(m\) 个，\(i\) 和 \(i+1\) 之间的距离为 \(d_i\)。

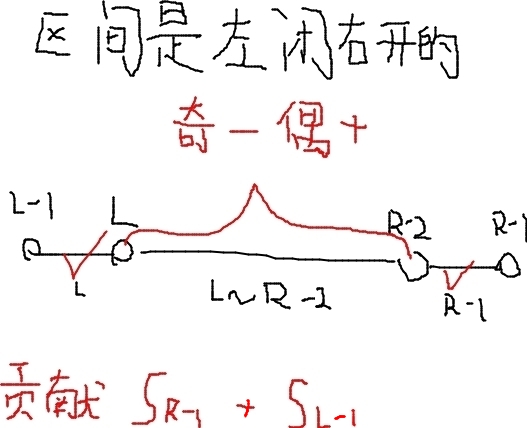
则问题为： 序列 \(d\) 长为 \(m-1\)，对于 \(k\le\dfrac m 2\)，求选出 \(k\) 个 \(d\) 中的元素，使得 \(d_i,d_{i+1}\) 不同时被选，求选的元素的和的最小值。

是个经典的反悔贪心，考虑费用流的增广路，发现一定形如由选 \(\{2,4\}\) 变为选 \(\{1,3,5\}\)。

用堆维护贡献，再用链表维护哪段 \(ab\) 已经被连在一起。

具体见代码。

int m=buc[id].size();
for(int i=1;i<m;i++)
{
	d[i]=buc[id][i]-buc[id][i-1];
	s[i]=d[i]-s[i-1];
}
for(int i=1;i<=m;i++)
{
	lst[i]=i-1;
	nxt[i]=i+1;
}
for(int i=1;i<m;i++)
{
	q.push(tii(d[i],i,i+1));
}
for(int i=1;i<=(m>>1);i++)
{
	auto [v,x,y]=q.top();
	q.pop();
	if(lst[y]!=x||nxt[x]!=y){
		i--;
		continue;
	}
	ans[i]=ans[i-1]+v;
	int L=lst[x],R=nxt[y];
	nxt[L]=R;
	lst[R]=L;
	if(L&&R<=m){
		q.push(tii(s[R]+s[L-1]-(s[nxt[y]]+s[y-1])-(s[x]+s[lst[x]-1]),L,R));
	}
}

每一层求出 \(ans\) 后，根据费用流结论，每一层的 \(ans\) 都是凸的，闵可夫斯基和合并即可（其实就是按斜率排序）。

AC Record

---

T3

鸽了，不会。