[NOIP2010 提高组] 引水入城:一道贪心、DP、搜索三不误的好题
[NOIP2010 提高组] 引水入城
一道贪心、DP、搜索三不误的好题
内容:区间覆盖、DP、DFS
传送门:https://www.luogu.com.cn/problem/P1514
题目背景
NOIP2010 提高组 T4
题目描述
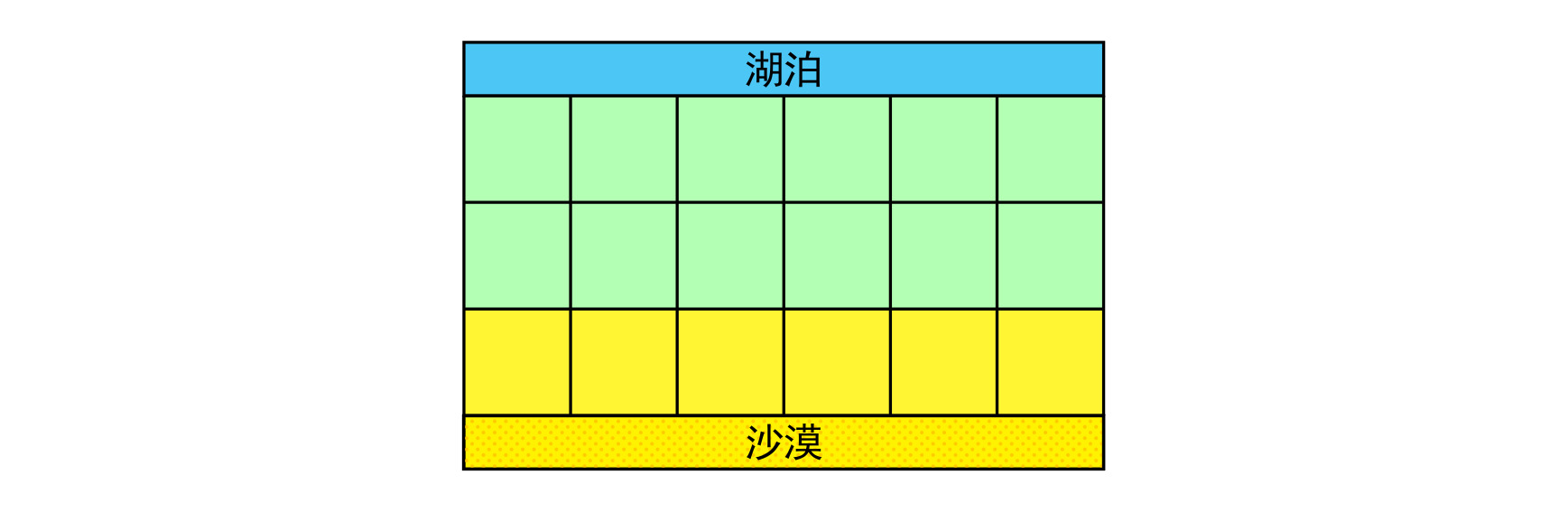
在一个遥远的国度,一侧是风景秀美的湖泊,另一侧则是漫无边际的沙漠。该国的行政区划十分特殊,刚好构成一个 \(N\) 行 \(M\) 列的矩形,如上图所示,其中每个格子都代表一座城市,每座城市都有一个海拔高度。
为了使居民们都尽可能饮用到清澈的湖水,现在要在某些城市建造水利设施。水利设施有两种,分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。
因此,只有与湖泊毗邻的第 \(1\) 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差,将湖水从高处向低处输送。故一座城市能建造输水站的前提,是存在比它海拔更高且拥有公共边的相邻城市,已经建有水利设施。由于第 \(N\) 行的城市靠近沙漠,是该国的干旱区,所以要求其中的每座城市都建有水利设施。那么,这个要求能否满足呢?如果能,请计算最少建造几个蓄水厂;如果不能,求干旱区中不可能建有水利设施的城市数目。
输入格式
每行两个数,之间用一个空格隔开。输入的第一行是两个正整数 \(N,M\),表示矩形的规模。接下来 \(N\) 行,每行 \(M\) 个正整数,依次代表每座城市的海拔高度。
输出格式
两行。如果能满足要求,输出的第一行是整数 \(1\),第二行是一个整数,代表最少建造几个蓄水厂;如果不能满足要求,输出的第一行是整数 \(0\),第二行是一个整数,代表有几座干旱区中的城市不可能建有水利设施。
样例 #1
样例输入 #1
2 5
9 1 5 4 3
8 7 6 1 2
样例输出 #1
1
1
样例 #2
样例输入 #2
3 6
8 4 5 6 4 4
7 3 4 3 3 3
3 2 2 1 1 2
样例输出 #2
1
3
提示
样例 1 说明
只需要在海拔为 \(9\) 的那座城市中建造蓄水厂,即可满足要求。
样例 2 说明

上图中,在 $3 $ 个粗线框出的城市中建造蓄水厂,可以满足要求。以这 $3 $ 个蓄水厂为源头在干旱区中建造的输水站分别用 \(3\) 种颜色标出。当然,建造方法可能不唯一。
数据范围
本题有 10 个测试数据,每个数据的范围如下表所示:
| 测试数据编号 | 能否满足要求 | \(N\le\) | \(M\le\) |
|---|---|---|---|
| 1 | 不能 | \(10\) | \(10\) |
| 2 | 不能 | \(100\) | \(100\) |
| 3 | 不能 | \(500\) | \(500\) |
| 4 | 能 | \(1\) | \(10\) |
| 5 | 能 | \(10\) | \(10\) |
| 6 | 能 | \(100\) | \(20\) |
| 7 | 能 | \(100\) | \(50\) |
| 8 | 能 | \(100\) | \(100\) |
| 9 | 能 | \(200\) | \(200\) |
| 10 | 能 | \(500\) | \(500\) |
对于所有 10 个数据,每座城市的海拔高度都不超过 \(10^6\)。
题目分析
根绝题意,我们可以构造出一个 \(n\times m\) 的矩阵,并且第一行的城市可以作为水源,最后一行的城市作为干旱的城市。
因此,这道题就可以被简述为:给定一个 \(n\times m\) 的矩阵,每个城市有一个数值 \(high[i][j]\) 代表这个城市的高度,请求出最少从第一行的几个城市出发,可以走遍所有的最后一行格子,满足每一步只能走到比自己更低的城市上。如果无解,则求出有多少个最后一行的城市无法被走到。
第一问:搜索(这里使用DFS)
由于我们知道了出发点,所以很容易想到使用搜索来求出从第一行的所有城市出发,搜索能走道的位置,并且给走过的位置做出标记。
这样一来,如果答案是无解的,那么我们结束搜索之后只需要遍历一遍最后一行看有多少城市是没有被标记的就行。
代码片段如下:
int n,m;
int high[505][505];
int dx[]={1,0,-1,0};
int dy[]={0,1,0,-1};
void dfs(int x,int y)
{
vis[x][y]=1;
for(int i=0;i<4;i++)
{
int next_x=x+dx[i];
int next_y=y+dy[i];
if(next_x<1||next_y<1||next_x>n||next_y>m||high[next_x][next_y]>=high[x][y]) continue; //越界or不满足水流条件就continue
if(!vis[next_x][next_y]) dfs(next_x,next_y); //没有被标记就走下去
}
}
显然,当搜索结束之后,我们只需要遍历一遍最后一行的城市,如果发现了存在没有访问的城市,就说明无解,这时候用一个ans来统计有多少城市没有被标记就行。
如果你写到这里,恭喜你,你能成功地搞到30分了:

但是怎能满足于此呢?
第二问:DP+区间覆盖(贪心)
我们不得不考虑一下,如果这组数据有解,那么我们该怎样求出最少建造多少水源能做到全部覆盖呢?
根据题意,我们容易联想到:既然可以不用所有一线城市就能做到提供满水流,说明水流流到最后一行的时候肯定存在重复流的情况。
根据这个,我们就把问题转化为了:把每一个一线城市的水流可以覆盖的地方都统计下来,然后求出来虽少用多少水源能覆盖所有的末线城市。
可是该怎么统计呢?如果是暴力枚举的话显然复杂度会爆表,所以我们不妨设想:如果每个一线城市流出的水流覆盖到的末线城市都是连续的,我们就把问题成了耳熟能详的:\(区间覆盖\) 问题,也就是给出若干个区间,求出最少多少个区间能覆盖所有末线城市。
这时候肯定会有人问了:“如果每个城市的水流覆盖不是连续的话,是不是就不能用区间覆盖了呢?” 的确,但是接下来,我们不妨证明一下,如果问题有解,那么每个水源最后覆盖的末线城市一定是 \(连续的\)。
假设存在如下情况(前提:有解):

粉色的是水流可以流经的地方,紫色是不可以流经的地方。显然在这种情况下,最后一行的城市只有左右两个城市可以被这个水源覆盖。既然我们是建立在有解的条件下讨论,所以一定会存在下图情况:

也就是说,一定会有另一条水流,流入粉色水流围起来的区域,然后流到最后一排,这样子才能保证粉色水流两个端点之间的城市能有水流覆盖。
然而,这里出现了一个矛盾之处:我们观察两条水流的交点(绿色的格子),既然青色水流能经过交点从右边流到左边,说明交点处的城市高度一定是高于左边相邻的城市的,但是如果这样的话,那么粉色水流在一开始流经绿色格子的时候,肯定就会经过绿色格子流到左边啊!这与我们一开始假设的粉色水流产生了矛盾。
所以如果题目有解,一定不会存在一个水源覆盖的城市是不连续的情况。也就是说:
这是本题最关键的结论,只有直到了这个,我们才能在接下来的操作中引入DP和区间覆盖。
寻找区间:DFS+DP
欢迎来到本题最精华的部分。对于区间问题,我们只需要统计出每个水源能流到最后一行城市的最大左端点和最大右端点即可。
这里我们便可以引入DP!我们定义两个数组 \(l[i][j]\) 和 \(r[i][j]\) 分别用来表示水流从城市 \((i,j)\) 出发最后可以流到的最后一行的最左边和最右边。这样我们在统计的时候,只需要遍历一遍第一行的所有城市就可以知道每个水源能覆盖最后一行的区间了。
因此,我们可以在递归搜索的时候,在回溯阶段加上给 \(l[i][j]\) 和 \(r[i][j]\) 的赋值即可,这样一旦搜索到了最后一行的点,开始回溯的时候就会把这个点的坐标一轮一轮地传递给上一个点,直到传递给第一行的水源处。
很明显的DP思路,所以我们可以思考一下如何给 \(l[i][j]\) 和 \(r[i][j]\) 赋值。
因为分别要找最左边端点和最右边端点,所以我们可以加入如下语句:
l[i][j]=min(l[i][j],l[next_x][next_y]);
r[i][j]=max(r[i][j],r[next_x][next_y]);
相当于让这个格子的 \(l[i][j]\) 和 \(r[i][j]\) 和接下来要走(前提是能走)的格子进行比较,选出更左和更右的值进行更新,这样传给上一层回溯的时候就能保证选到的左右端点是最左和最右的。
显然,这两个数组里面的值存的是城市在这一行的列标,因为我们要把这个当成一维的区间处理。
于是我们将DP式子塞进DFS里面,就能得到如下完整搜索代码:
int n,m;
int high[505][505];
int l[505][505],r[505][505];
int dx[]={1,0,-1,0};
int dy[]={0,1,0,-1};
void dfs(int x,int y)
{
vis[x][y]=1;
for(int i=0;i<4;i++)
{
int next_x=x+dx[i];
int next_y=y+dy[i];
if(next_x<1||next_y<1||next_x>n||next_y>m||high[next_x][next_y]>=high[x][y]) continue;
//越界or不满足水流条件就continue↑
if(!vis[next_x][next_y]) dfs(next_x,next_y);
//没有被标记就走下去↑
l[x][y]=min(l[x][y],l[next_x][next_y]);
r[x][y]=max(r[x][y],r[next_x][next_y]);
//这里为什么没有把DP式子放在if里面呢?那是因为就算接下来要走的格子已经搜索过了,也要更新一下左右端点,来保证每个搜索到的格子所存入的值都是最优解。
}
}
统计区间:区间覆盖(贪心)
在DFS的过程中,我们已经找到了所有水源能覆盖的最后一行城市的区间,因此对于有解的情况,我们把问题转化成了寻找最少的区间数,使得这些区间能覆盖满最后一行的城市。这就要引入区间覆盖的问题了。
我们考虑这样一个问题:
给定若干线段,试求出最少用多少线段能完全覆盖一段固定区间。
想要求出这个问题,我们就需要引入贪心策略,既然想要找到尽可能少的线段,那我们每找一个线段就让他尽可能覆盖的长一点就可以了!
更具体地阐述就是:在满足线段左端点能盖住区间的左端点(也就是满足线段的左端点在区间左端点的左边)的所有线段里,找到一个右端点最大的线段作为这一次覆盖选用的线段,然后更新新的区间左端点为这个线段的右端点,继续在剩下所有的线段里面找到满足上述要求的线段,直到找到的线段右端点大于区间的右端点为止,每找到一个符合要求的线段就让答案加一。
我们发现本题的方法和这个完全一致,且第一行城市对应的 \(l[1][j]\) 和 \(r[1][j]\) 就是对应的所有线段的左右端点!
对于这道题来说,只要有解就说明一定能找到若干个线段覆盖所有最后一行的城市,所以在这里无需讨论线段不够覆盖的问题。但是特别地,对于其他题目,还是有必要在每一次选取线段的时候额外判断:如果这一轮循环没有找到符合要求的线段,那么直接代表无解,跳出循环。
至于为什么这个策略是最优的。这里给出一个比较形象但未必严谨的证明,严禁证明之后有机会我会补充在本帖最后。
形象证明:
假设有一条更长的线段可以替代原来至少两个线段,我们剔除这两个原来的线段,如果这几条线段连续,则应当保证这条长线段的左右端点贴上去之后不会露出空隙,也就是说明这个长线段的左端点同样符合上述贪心策略里的覆盖条件,并且右端点还更大,所以按理来说是应该在执行贪心策略的时候就已经被选用的!与假设矛盾。如果这几个线段不连续,说明这个长线段覆盖上去的时候会盖住更多线段,所以相当于变相的盖住了更多的端线段,根据上述论证,同样与假设矛盾。说明只存在一换多的情况是不存在的。
假设从最左侧的线段开始数起,第一个真正的最优解和算法最优解的线段选择不同的线段为线段 \(a\) 和 \(b\),根据算法策略,算法找到的区间右端点一定大于最优解找到的右端点,因此用算法找到的线段 \(b\) 来代替最优解的线段 \(a\),仍然满足全部覆盖,并且仍然是最优解,之后每一个线段都遵循同样的替代方式,由于线段是一换一,所以贪心算法找到的结果和最优解数量是一致的。
综上,该策略最优。
最后,我们只需要输出统计完的线段数即可!
AC代码奉上:
#include <bits/stdc++.h>
using namespace std;
bool vis[505][505];
int high[505][505];
int l[505][505],r[505][505];
int dx[]={1,0,-1,0};
int dy[]={0,1,0,-1};
#define inf 1000006
int n,m;
void dfs(int x,int y)
{
vis[x][y]=1;
for(int i=0;i<4;i++)
{
int next_x=x+dx[i];
int next_y=y+dy[i];
if(next_x<1||next_y<1||next_x>n||next_y>m||high[next_x][next_y]>=high[x][y]) continue;
if(!vis[next_x][next_y]) dfs(next_x,next_y);
l[x][y]=min(l[x][y],l[next_x][next_y]);
r[x][y]=max(r[x][y],r[next_x][next_y]);
}
}
int main()
{
cin>>n>>m;
memset(l,inf,sizeof(l));
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
{
cin>>high[i][j];
if(i==n)
{
l[i][j]=j;
r[i][j]=j;
//把最后一排的编号初始化,用来存左右端点
}
}
}
bool flag=0;
for(int j=1;j<=m;j++)
{
if(!vis[1][j]) dfs(1,j);
}
int ans=0;
for(int j=1;j<=m;j++)
{
if(!vis[n][j])
{
flag=1;
ans++;
}
}
if(flag)
{
cout<<0<<endl;
cout<<ans<<endl;
return 0;
}
int Left=1,Right=r[1][1];
while(Left<=m) //只要被覆盖完就一直覆盖
{
for(int i=1;i<=m;i++) //把m个线段都遍历一遍
{
if(l[1][i]<=Left) Right=max(Right,r[1][i]);
//如果满足左端点要求,就开始找右端点最大的线段↑
}
Left=Right+1; //找到线段之后记得更新区间的左端点
ans++; //答案别忘了加一
}
cout<<1<<endl<<ans<<endl; //输出答案,结束喵
}
毫无疑问的:

总而言之,这道题在我看来是一道不错的搜索+DP+贪心综合练习题,姑且配得上蓝题的头衔,正解对于初学者来说也算好理解。
最后,哀寂和洞烛镇楼捏(逃




 浙公网安备 33010602011771号
浙公网安备 33010602011771号