每日一题_191012

在平面四边形\(ABCD\)中,已知\(AB=1\),\(AC=\sqrt{5}\),\(BD\perp BC\),\(BD=2BC\),则\(AD\)的最小值为\(\underline{\qquad\qquad}.\)
解析:
法一 如图,固定\(AC\)边长,则点\(B\)在以\(A\)点为圆心,以\(1\)为半径的圆上运动,


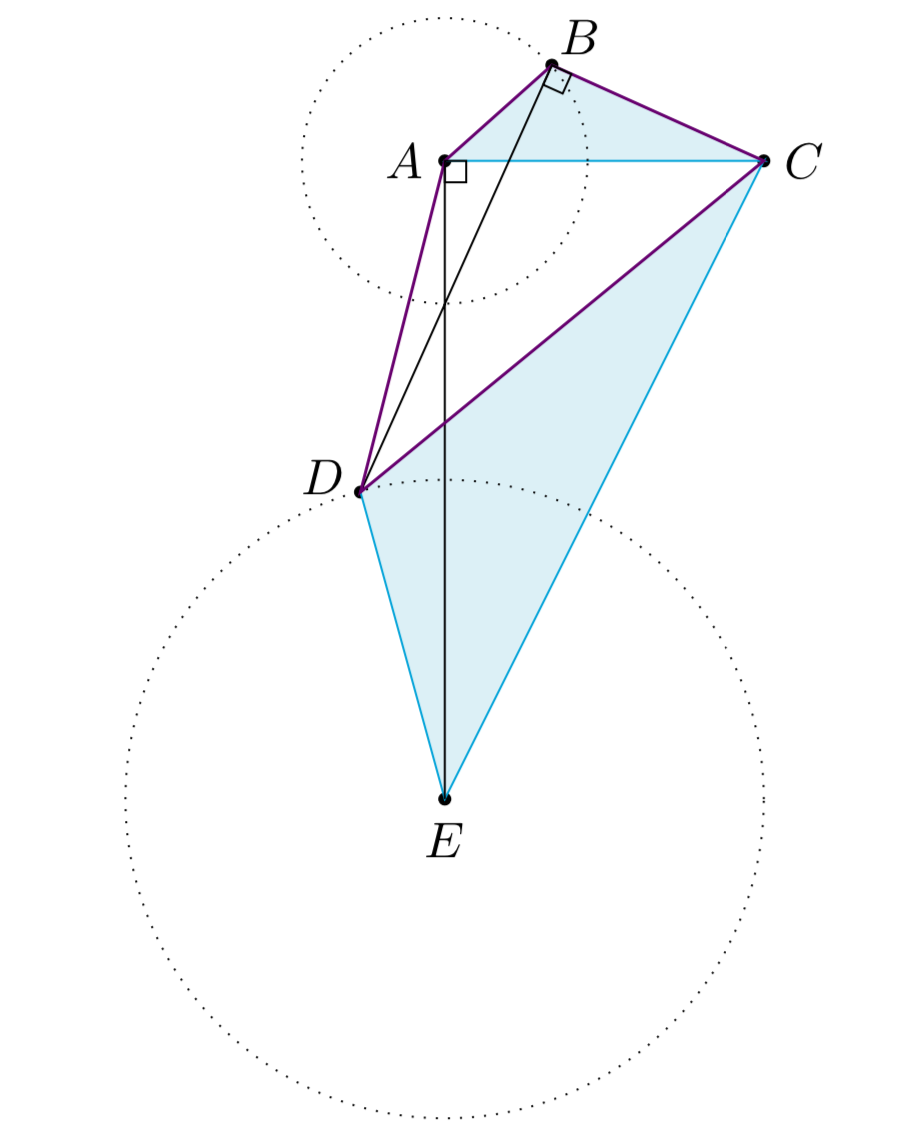
若记$\angle BCD=\theta$,则$D$点在以$E$点为圆心,以$\sqrt 5$为半径的圆上运动,其中$EA\perp CA$,且$$EA=2CA=2\sqrt{5},$$所以当$D$位于线段$EA$上时$AD$取得最小值$\sqrt 5$. 法二 由题,设$BC=x$,则$$ BD=2x,CD=\sqrt{5}x.$$于是由托勒密不等式可得$$ AD\cdot BC+AB\cdot CD\geqslant AC\cdot BD.$$解得$AD\geqslant 5$.上述不等式当且仅当$A,B,C,D$四点共圆时取等.因此$AD$最小值为$\sqrt5$.