已知函数\(f(x)=x^3+ax^2+bx\)有两个极值点\(x_1,x_2\),且\(x_1<x_2\),若\(x_1+2x_0=3x_2\),则函数\(g(x)=f(x)-f(x_0)\)的零点个数情况为\((\qquad)\)
\(\mathrm{A}.\)恰有\(1\)个零点
\(\mathrm{B}.\)恰有\(2\)个零点
\(\mathrm{C}.\)恰有\(3\)个零点
\(\mathrm{D}.\)零点个数不确定
解析: 引理\(:\) 三次函数的对称性 \(\mathrm{II} \qquad\) 设$$f(x)=ax3+bx2+cx+d ,a\ne 0.$$的极大值为\(M\)，方程\(f\left( x \right) = M\)的两根为$$x_1,x_2, (x_1<x_2)，$$则区间\(\left[ x_1,x_2 \right]\) 被 \(-\dfrac{b}{3a}\)和极小值点三等分．
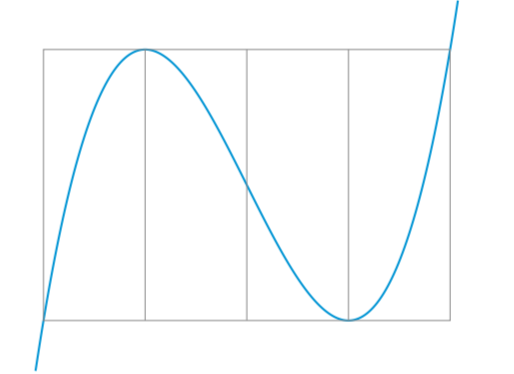
记三次函数的极小值点为$x_3$，则$$x_1+x_3=-\dfrac{2b}{3a}.$$ 另一方面$f(x)=M=f(x_1)$得$$a(x^3-x_1^3)+b(x^2-x_1^2)+c(x-x_1)=0,$$整理得$$(x-x_1)\left[ax^2+(ax_1+b)x+(ax_1^2+bx_1+c)\right]=0,$$由韦达定理有$$x_1+x_2=-\dfrac{ax_1+b}{a},$$所以有$2x_1+x_2=-\dfrac ba$，于是引理得证. 回到原题我们可知$$x_0=\dfrac{3}{2}x_2-\dfrac{1}{2}x_1=x_2+\dfrac{1}{2}\left(x_2-x_1\right).$$结合三次函数的对称性$\mathrm{II}$可知$$f(x_1)=f(x_0),x_1\neq x_0,$$所以$g(x)=f(x)-f(x_0)$的有且仅有两个零点.