代码手记笔录——并查集

并查集

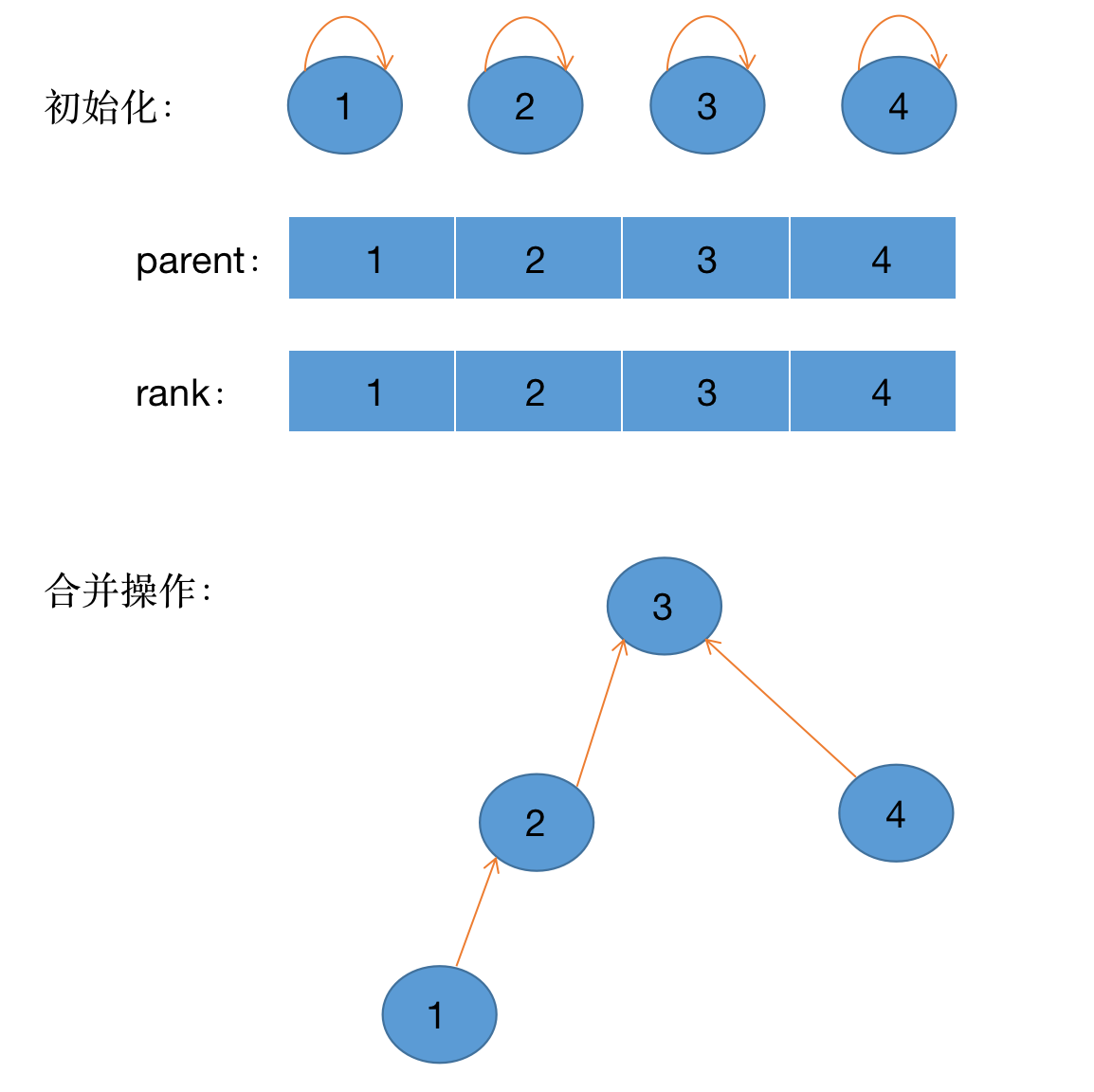
（1）初始化：2个数组，一个标记节点i的父节点，一个标记以节点i为父节点的树深。初始时，所有节点的根节点指向自身；
（2）查找：如果结点i的父节点不等于自身，一直说明当前结点不是根节点，需要一直往上溯源while(p != parent[p]) p = parent(p);；
（3）并集：若节点p与节点q的根节点一致，说明已经处于同一个集合，无需并集操作；否则，分别找到节点p、节点q所属的根节点，将树深小的挂在树深大上；若二者树深相同，不妨让节点p所属的树挂在节点q所属的树，并使q的树深+1；
（4）判断是否相连：若节点p与节点q指向同一个根节点，则两结点相连；否则不相连。
并查集demo代码：

class UnionFind {
    vector<int> rank;
    vector<int> parent;
    UnionFind(int n) {
        rank.resize(n);
        parent.resize(n);
        for (int i=0; i<n; ++i) {
            rank[i] = i;
            parent[i] = i;
        }
    }
    int find(int p) {
        while (p != parent[p])
            p = parent[p];
        return parent[p];
    }
    bool isConnected(int p, int q) {
        return find(p) == find(q);
    }
    void unionElement(int p, int q) {
        if (parent[p] == parent[q])
            return;
        int pRoot = parent[p];
        int qRoot = parent[q];
        if (rank[p] < rank[q])
            rank[p] = qRoot;
        else if (rank[q] < rank[p])
            rank[q] = pRoot;
        else {
            rank[p] = qRoot;
            rank[q] += 1;
        }
    }
}

200. 岛屿数量

方法一：深度搜索

若当前位置为'1'，则将设置为'0'，并将其上下左右为'1'的位置也置为'0'。主函数遍历grid，判断有多少次最开始调用dfs()

class Solution {
public:
    int cnt;
    int numIslands(vector<vector<char>>& grid) {
        int m = grid.size(), n = grid[0].size();
        cnt = 0;
        for (int i=0; i<m; ++i) {
            for (int j=0; j<n; ++j) {
                if (grid[i][j] == '1') {
                    dfs(grid, i, j);
                    ++cnt;
                }
            }
        }
        return cnt;
    }
    void dfs(vector<vector<char>>& grid, int i, int j) {
        int m = grid.size(), n = grid[0].size();
        grid[i][j] = '0';
        if (i-1>=0 && i-1<m && grid[i-1][j] == '1')
            dfs(grid, i-1, j);
        if (i+1>=0 && i+1<m && grid[i+1][j] == '1')
            dfs(grid, i+1, j);
        if (j-1>=0 && j-1<n && grid[i][j-1] == '1')
            dfs(grid, i, j-1);
        if (j+1>=0 && j+1<n && grid[i][j+1] == '1')
            dfs(grid, i, j+1);
    }
};

方法二：并查集

岛屿问题是典型的并查集问题。如果当前为‘1’，判断上下左右位置是否也为'1'，若是，则进行合并操作。

class UnionFind {
private:
    vector<int> rank;
    vector<int> parent;
    int cnt;
public:
    UnionFind(vector<vector<char>>& grid) {
        int m = grid.size(), n = grid[0].size(), idx;
        cnt = 0;
        parent.resize(m*n);
        rank.resize(m*n);
        for (int i=0; i<m; ++i) {
            for (int j=0; j<n; ++j) {
                idx = i*n + j;
                rank[idx] = 1;
                if (grid[i][j] == '1') {
                    parent[idx] = idx;
                    ++cnt;
                }
                else
                    parent[idx] = -1;
            }
        }
    }
    int find(int p) {
        while (parent[p] != p)
            p = parent[p];
        return parent[p];
    }
    void unionElement(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot)
            return;
        if (rank[pRoot] < rank[qRoot])
            parent[pRoot] = qRoot;
        else if (rank[qRoot] < rank[pRoot])
            parent[qRoot] = pRoot;
        else {
            parent[pRoot] = qRoot;
            rank[qRoot] += 1;
        }
        --cnt;
    }
    const int getCnt() {
        return cnt;
    }
};

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int m = grid.size(), n = grid[0].size();
        UnionFind uf(grid);
        for (int i=0; i<m; ++i) {
            for (int j=0; j<n; ++j) {
                if (grid[i][j] == '1') {
                    grid[i][j] = 0;
                    if (i-1>=0 && grid[i-1][j] == '1')
                        uf.unionElement(i*n+j, (i-1)*n+j);
                    if (i+1<m && grid[i+1][j] == '1')
                        uf.unionElement(i*n+j, (i+1)*n+j);
                    if (j-1>=0 && grid[i][j-1] == '1')
                        uf.unionElement(i*n+j, i*n+j-1);
                    if (j+1<n && grid[i][j+1] == '1')
                        uf.unionElement(i*n+j, i*n+j+1);
                }
            }
        }
        return uf.getCnt();
    }
};

684 冗余连接

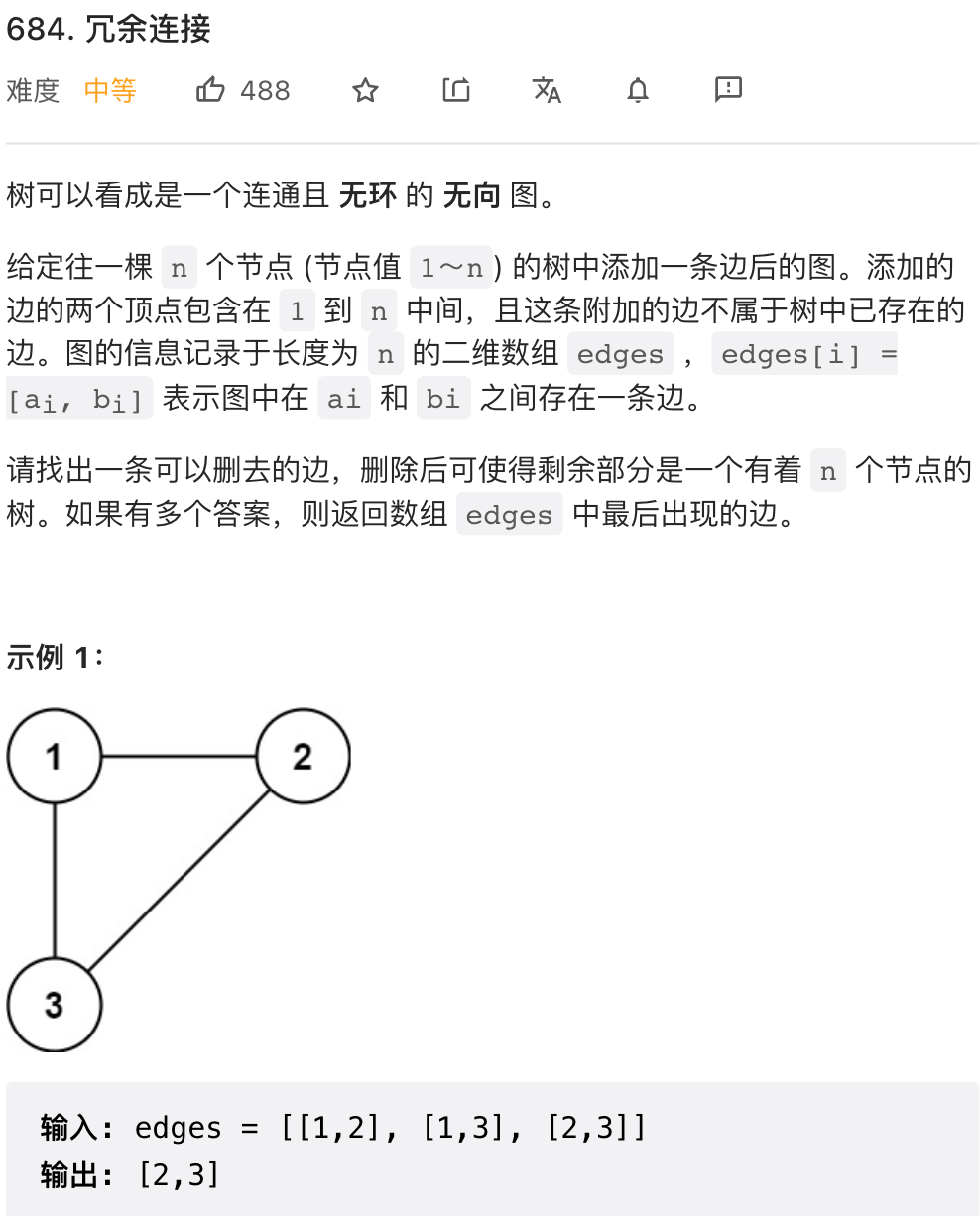
class Solution {
public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        int n = edges.size();
        vector<int> parent(n+1, 0);
        vector<int> rank(n, 1);
        vector<int> ans(2,0);
        for (int i=0; i<n; ++i)
            parent[i] = i;
        for (auto edge : edges) {
            int pf = edge[0], pc = edge[1];
            int pfRoot = find(parent, rank, pf);
            int pcRoot = find(parent, rank, pc);
            // 如果将同一个集的元素进行拼接，必定会成环
            if (pfRoot == pcRoot)
                return edge;
            unionSet(parent, rank, pf, pc);
        }
        return ans;
    }

private:
    int find(vector<int> &parent, vector<int> &rank, int idx) {
        if (parent[idx] != idx)
            parent[idx] = find(parent, rank, parent[idx]);
        return parent[idx];
    }
    void unionSet(vector<int> &parent, vector<int> &rank, int p1, int p2) {
        int pRoot1 = find(parent, rank, p1);
        int pRoot2 = find(parent, rank, p2);
        if (rank[pRoot1] < rank[pRoot2])
            parent[pRoot1] = parent[pRoot2];
        else
            parent[pRoot2] = parent[pRoot1];
        rank[pRoot1] = rank[pRoot1]==rank[pRoot2] ? rank[pRoot1] + 1 : rank[pRoot1];
    }
};