代码手记笔录——递归回溯
递归回溯的两种写法
(1)递归回溯无非是向下走一直到递归基,然后向右走。这个 向右 的过程可以通过 for 循环控制 (迭代向右法) ,也可以通过控制下标递归控制 (下标递归向右法)
(2)递归回溯函数里的 push() 与 pop() 个数一定是相等的。【注意:if-else里的 pop() 只能算一次】
(3)为减少递归-回溯的时间,优化的方法是 剪枝
(4)递归回溯步骤是向下-向右,其实就暗含着搜索答案存在 可以向右 的性质。对于给定的不满足 向右递归就可以搜索到全部答案 数组,首先要让该数组满足该条件。如对求 sum 的组合元素需 先对 nums 进行排序: 【39 组合总和 】、【40 组合总和 II】
(5)递归回溯为了避免 ans 的答案出现重复,需在 向右走 的时候进行处理,跳过会出现重复答案的搜索路径。如【40 组合总和 II】
(6)对于某些题目,在到达向下递归基时,无需向右走。【93 复原 IP 地址】
迭代向右法
迭代向右法模板如下:【push() 与 pop() 个数需相等】
void backtracking(vector<vector<int>> &ans, vector<int> &item, int idx, int n, int k) {
if (...) // 向右递归出口
return;
for (....) { // (含剪枝条件)// for 循环向右同层递归
item.push_back(curIdx); // 若不是出口就可以直接 push_back
if (...) { // 如果满足条件
ans.push_back(item);
item.pop_back(); // push() 与 pop() 对应
return;
}
backtracking(ans, item, curIdx+1, n, k); // 从上到下走
item.pop_back(); // push() 与 pop() 对应
}
}
章节题目总结
39 组合总和
这道题与 47 全排列 II 一起看,无论是组合还是排列,都需要先对 nums 进行排序
class Solution {
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> ans;
vector<int> item;
// 这道题有点坑,我们在进行操作之前必须使得给定数组是升序排序的
sort(candidates.begin(), candidates.end());
backtracking(ans, item, 0, candidates, target);
return ans;
}
private:
void backtracking(vector<vector<int>> &ans, vector<int> &item, int idx, vector<int>& candidates, int target) {
if (idx >= candidates.size())
return;
int curNum = candidates[idx];
// 采用push-pop结构
item.push_back(curNum);
target -= curNum;
if (target <= 0) { // 停止向下递归
if (target == 0)
ans.push_back(item);
item.pop_back();
target += curNum;
}
else {
backtracking(ans, item, idx, candidates, target); // 向下递归
item.pop_back();
target += curNum;
backtracking(ans, item, idx+1, candidates, target); // 向右边递归
}
}
};
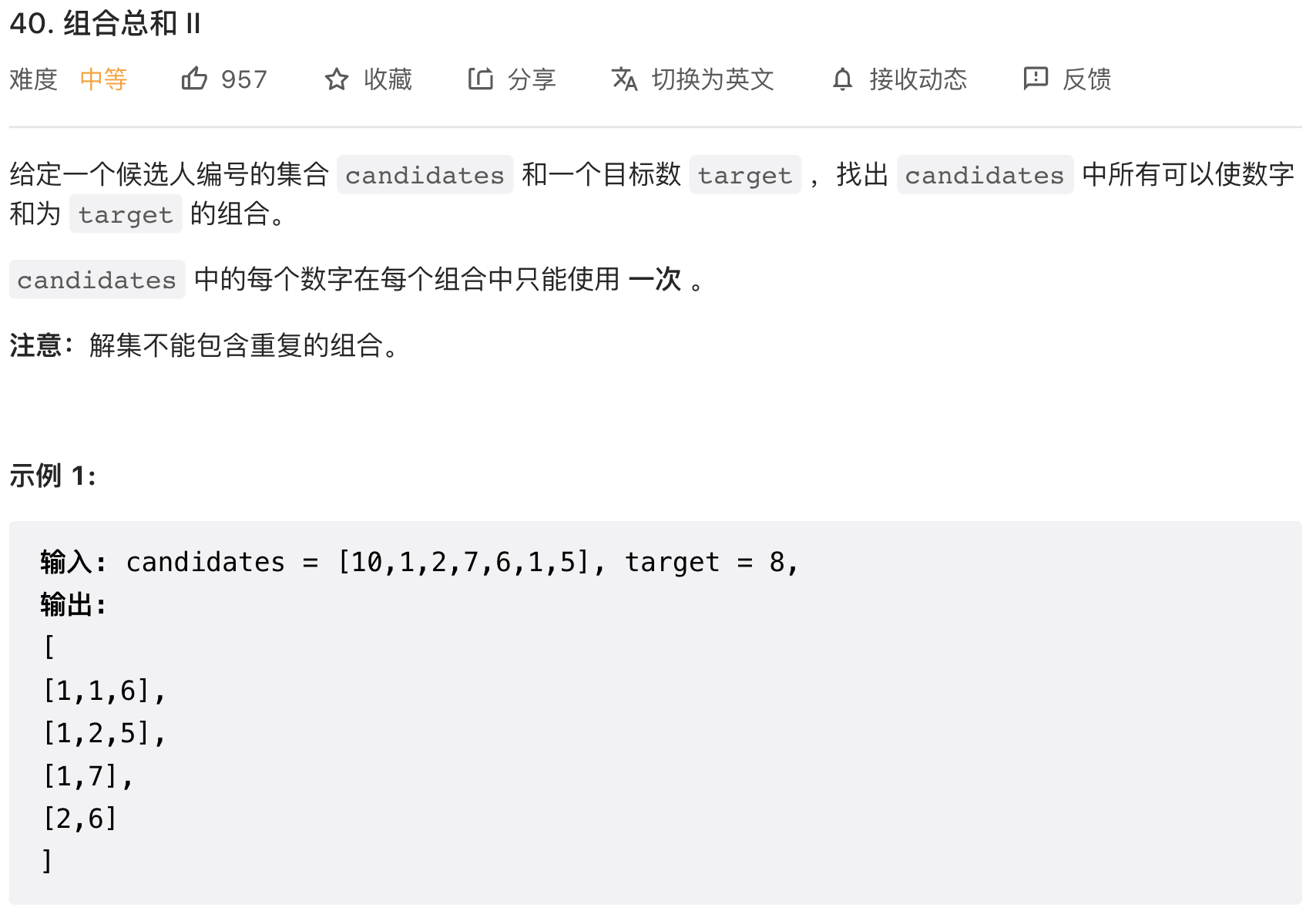
40 组合总和 II
备注:排序预处理+while() 向右走的策略防止答案重复
class Solution {
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
vector<vector<int>> ans;
vector<int> item;
sort(candidates.begin(), candidates.end());
backtracking(ans, item, 0, candidates, target);
return ans;
}
private:
void backtracking(vector<vector<int>> &ans, vector<int> &item, int idx, vector<int>& candidates, int target) {
if (idx >= candidates.size())
return;
int curNum = candidates[idx];
item.push_back(curNum);
target -= curNum;
if (target <= 0) {
if (target == 0)
ans.push_back(item);
item.pop_back();
}
else {
backtracking(ans, item, idx+1, candidates, target);
item.pop_back();
target += curNum;
int tmpIdx = idx+1;
while (tmpIdx<candidates.size() && candidates[tmpIdx] == candidates[idx])
++tmpIdx;
backtracking(ans, item, tmpIdx, candidates, target);
}
}
};
下标递归向右法
下标递归向右法模板如下:
void backtracking(vector<vector<int>> &ans, vector<int> &item, int idx, int n, int k) {
if (...) // (含剪枝条件)向右递归出口
return;
item.push_back(idx); // 若不是出口就可以直接 push_back
if (....) { // 不满足一组递归答案,继续向下递归
backtracking(ans, item, idx+1, n, k); // 从上到下走
item.pop_back(); // 回溯
backtracking(ans, item, idx+1, n, k); // 从左到右走
}
else { // 到达向下递归出口,只继续向右递归
ans.push_back(item); // 记录一组答案
item.pop_back(); // 对 item.push_back(idx) 的呼应
backtracking(ans, item, idx+1, n, k); // // 从左到右走
}
}
章节题目总结
131 分割回文串【高频考题】
备注:(1)考点一:回文串 dp 的遍历顺序;(2)递归回溯
回文串的遍历顺序问题
首先回文字符串 dp 初始化矩阵为下三角矩阵,且元素只为 1:
for (int i=0; i<n; ++i) {
for (int j=i; j<n; ++j)
dp[i][j] = 1;
}
然后明确字符串 s[i:j] 是回文串的条件=>s[i]==s[j] && dpSys[i+1][j-1],即长元素 s[i:j] 的判定条件依赖于内部短元素 s[i+1:j-1]。因此遍历顺序应该从短字符串开始:
for (int i=0; i<n; ++i) {
for (int j=0; j<=i; ++j)
dpSyms[i][j] = 1;
}
for (int i=n-1; i>=0; --i) {
for (int j=i+1; j<n; ++j)
dpSyms[i][j] = (s[i] == s[j]) && dpSyms[i+1][j-1];
}
对于此类涉及字符的题目(对比【17 电话号码的字母组合】),适合用下标递归向右法。
备注:(1)竟然在 if(!cond) 犯迷糊,以后统一写 if(cond > 0);(2)如果整个字符串能被分割,idx 就会到达 n,否则不会到达 n;因此在向右递归出口 Push Into ans 是正确的。
class Solution {
public:
vector<vector<string>> ans;
vector<vector<string>> partition(string s) {
int n = s.size();
vector<vector<int>> dpSyms(n, vector<int>(n, 0));
init(dpSyms, s, n);
vector<string> item;
backtracking(dpSyms, item, s, 0);
return ans;
}
private:
void init(vector<vector<int>> &dpSyms, string s, int n) {
for (int i=0; i<n; ++i) {
for (int j=0; j<=i; ++j)
dpSyms[i][j] = 1;
}
for (int i=n-1; i>=0; --i) {
for (int j=i+1; j<n; ++j)
dpSyms[i][j] = (s[i] == s[j]) && dpSyms[i+1][j-1];
}
}
void backtracking(vector<vector<int>> &dpSyms, vector<string> &item, string &s, int idx) {
int n = s.size();
if (idx >= n) { // 向右走递归出口
if (item.size())
ans.push_back(item);
return;
}
for (int j=idx; j<n; ++j) { // 向右走
if (dpSyms[idx][j]) {
string curStr = s.substr(idx, j-idx+1);
item.push_back(curStr);
backtracking(dpSyms, item, s, j+1); // 向下走
item.pop_back();
}
}
}
};
93 复原 IP 地址
备注:(1)这道题在到达向右递归基时无需向右走;(2)IP 每部分的合法性判断
bool isValid(string s) {
// 空 || 长度大于3 || 含有前导 0
if (!s.size() || s.size()>3 || (s[0]=='0'&& s.size()>1))
return false;
int num = 0;
for (auto data : s)
num = num*10 + data - '0';
// 介于256-999
if (num > 255)
return false;
return true;
}
class Solution {
public:
vector<string> restoreIpAddresses(string s) {
vector<string> ans;
if (s.size() > 12)
return ans;
vector<string> itemStr;
backtracking(ans, itemStr, -1, 0, s);
return ans;
}
private:
void backtracking(vector<string> &ans, vector<string> &itemStr, int preIdx , int curIdx, string &s) {
if (curIdx >= s.size() || itemStr.size() >=4)
return;
string curNum = s.substr(preIdx+1, curIdx-preIdx);
if (!isValid(curNum))
return;
itemStr.push_back(curNum);
if (itemStr.size() == 4 && curIdx+1 >= s.size()) {
string ansStr;
for(int i=0; i<4; ++i) {
if (i !=0)
ansStr.push_back('.');
ansStr += itemStr[i];
}
ans.push_back(ansStr);
itemStr.pop_back();
return;
}
backtracking(ans, itemStr, curIdx, curIdx+1, s); // 向下移动
itemStr.pop_back();
backtracking(ans, itemStr, preIdx, curIdx+1, s); // 向右移动
}
bool isValid(string s) {
// 空 || 长度大于3 || 含有前导 0
if (!s.size() || s.size()>3 || (s[0]=='0'&& s.size()>1))
return false;
int num = 0;
for (auto data : s)
num = num*10 + data - '0';
// 介于256-999
if (num > 255)
return false;
return true;
}
};
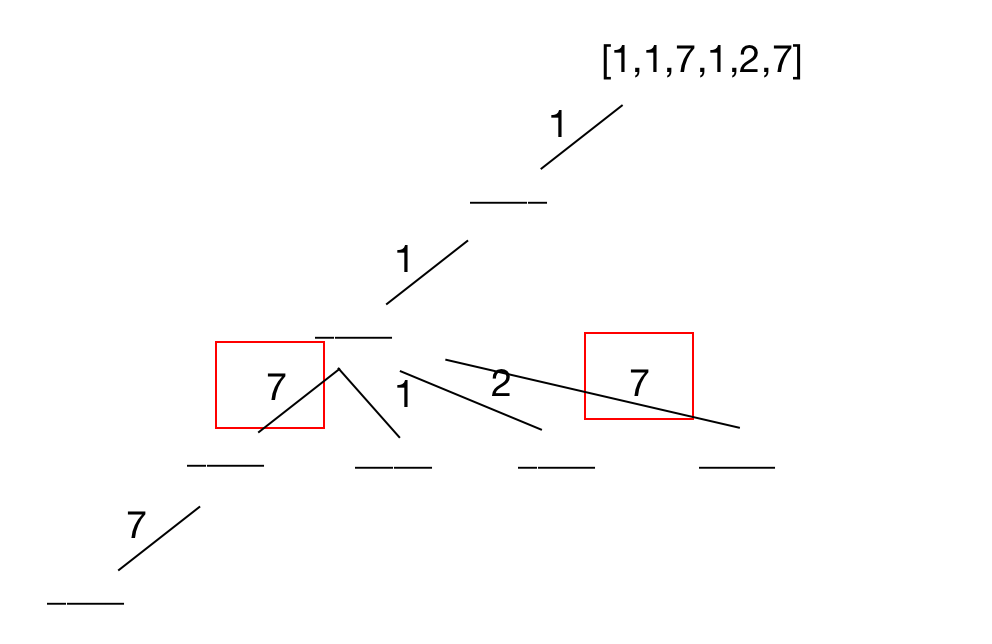
491 递增子序列
本题与 40 组合总和 II && 46 全排列 一起看。这两道题重点都是在去重上。 40 组合总和 II 可以先将所有元素进行排序sort(),以确保相同元素总是连续的。而本题无法排序预处理,在向右递归的时候,需要记住本层先前使用过的元素【使用数据结构 set
方法一:在进入递归函数前进行剪枝
备注:当时方法一花了好多时间,原因是向右递归选择元素的条件是 nextIdx 元素要大于等于 item 的最后元素 last 并且 nextIdx 未选过。因此,剪枝的条件是 nextIdx 元素小于 item ** OR ** nextIdx 被选择过。
class Solution {
public:
vector<vector<int>> ans;
vector<int> item;
vector<vector<int>> findSubsequences(vector<int>& nums) {
set<int> uset;
backtracking(0, INT_MIN, nums, uset);
return ans;
}
private:
void backtracking(int curIdx, int last, vector<int>& nums, set<int> &uset) {
int n = nums.size();
if (curIdx >= n)
return;
item.push_back(nums[curIdx]);
if (item.size() > 1)
ans.push_back(item);
int nextIdx = curIdx + 1;
while ((nextIdx < n) && (nums[nextIdx] < nums[curIdx]))
++nextIdx;
set<int> new_uset;
backtracking(nextIdx, nums[curIdx], nums, new_uset);
item.pop_back();
uset.insert(nums[curIdx]);
nextIdx = curIdx + 1;
while ((nextIdx < n) && ((nums[nextIdx] < last) || uset.count(nums[nextIdx])))
++nextIdx;
backtracking(nextIdx, last, nums, uset);
}
};
方法二:在进入递归函数后才进行剪枝
备注:若若当前元素与同层前面的元素相同,考虑右边的元素,直接剪枝,** return **。当时少了 return 条件。
class Solution {
public:
vector<vector<int>> ans;
vector<int> item;
vector<vector<int>> findSubsequences(vector<int>& nums) {
set<int> um;
backtracking(0, INT_MIN, nums, um);
return ans;
}
private:
// preIdx 表示上一次入 item 的序号, curIdx 表示在 nums 的序号
void backtracking(int curIdx ,int last, vector<int>& nums, set<int> &um) {
int n = nums.size();
if (curIdx >= n)
return;
// 若当前元素与同层前面的元素相同,考虑右边的元素
if (um.count(nums[curIdx]) > 0) {
backtracking(curIdx+1, last, nums, um);
return;
}
if (nums[curIdx] >= last) {
item.push_back(nums[curIdx]);
if (item.size() > 1)
ans.push_back(item);
set<int> um_null; // 下一层递归时,set 置空
backtracking(curIdx+1, nums[curIdx], nums, um_null);
item.pop_back();
um.insert(nums[curIdx]);
backtracking(curIdx+1, last, nums, um); // 向右递归
}
else {
backtracking(curIdx+1, last, nums, um); // 向右递归
}
}
};
46 全排列
本题与 40 组合总和 II && 491 递增子序列 一起看。
本题是 47. 全排列 II 简单版。
47. 全排列 II
本题与 剑指 Offer 38. 字符串的排列 一起看,基本一样,除了存储的数据结构不一致。
全排列的题目算法思想是根据给定的原始数据,先对其进行排序,然后每次在新 item 的末尾添加元素时,都对排序后的原始数据从左到右判断,该元素是否可以 append 进 item。
使用 used[i] 数据标记 当前元素 i 是否被使用过。判断的标准是:若元素 i 被挑选过,或者当前步骤否处于 “同一元素向右走” 的步骤(为了让 ans 无重复 item 元素),就判断下一个元素,直至满足条件。
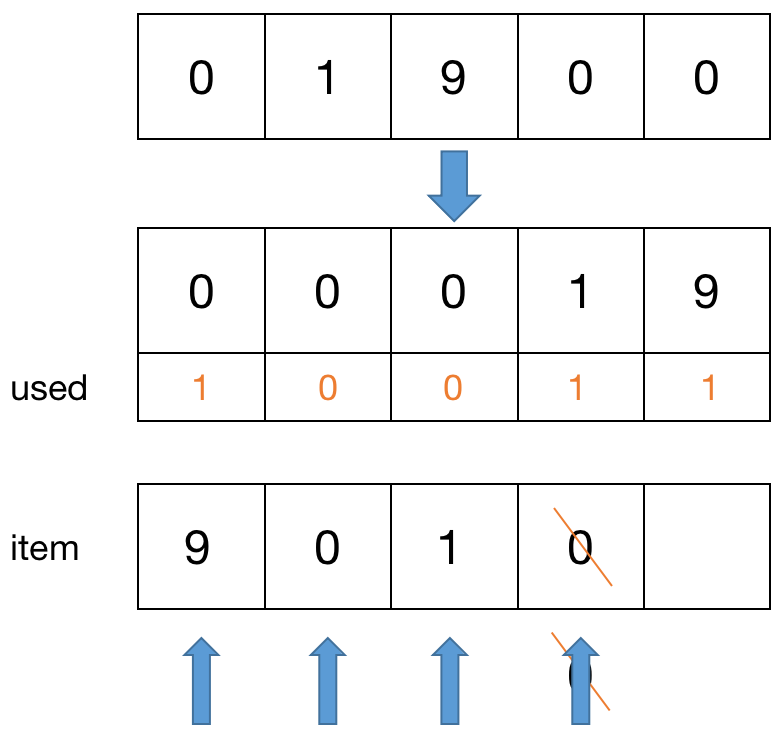
class Solution {
public:
vector<vector<int>> ans;
vector<vector<int>> permuteUnique(vector<int>& nums) {
int n = nums.size();
sort(nums.begin(), nums.end());
backtracking(nums, 0, 0);
return ans;
}
void backtracking(vector<int>& nums, int permIdx, int pickIdx) {
int n = nums.size(), nextIdx;
if (pickIdx >= n)
return;
swap(nums[permIdx], nums[pickIdx]);
if (permIdx >= n-1) {
ans.emplace_back(nums);
swap(nums[permIdx], nums[pickIdx]); // undo
return;
}
backtracking(nn, permIdx+1, permIdx+1); // 向下走
swap(nums[permIdx], nums[pickIdx]);
nextIdx = pickIdx + 1;
while (nextIdx < n && nums[nextIdx] == nums[pickIdx])
++nextIdx;
backtracking(nums, permIdx, nextIdx);
}
};





 浙公网安备 33010602011771号
浙公网安备 33010602011771号