图论学习九之Bipartite Graph

　　　　　　　　匹配

 

• 设G = <V, E>, 若E*(E*E)中任何两条边均不相邻,
　　• 则称E*为G中边独立集, 也称E*为G中的匹配(Matching);

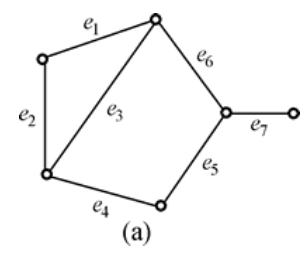
图(a)中， E*= { e1, e4, e7 }就是一个匹配。所谓任何两条边均不相邻，

通俗地讲，就是任何两条边都没有公共顶点。

 

若在E*中加入任意一条边所得集合都不是匹配, 则称E*为极大匹配;

边数最多的匹配称为最大匹配;

最大匹配的边数称为边独立数或匹配数, 记作β1(G), 简记为β1。

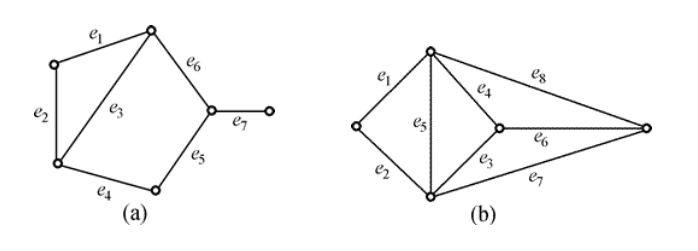
　　图(a)中, { e2, e6 }, { e3, e5 }, { e1, e4, e7 }都是极大匹配,
{ e1, e4, e7 }是最大匹配, β1 = 3。
　　图(b)中, { e1, e3 }, { e2, e4 }, { e4, e7 }都是极大匹配, 也
都是最大匹配, β1 = 2。

 

 

　　　　　　　　二部图(二分图)

二部图：如果图G是一个简单图，它的顶点集合V是由两个没
有公共元素的子集X={X1,X2,..,Xm}与子集Y={Y1,Y2,…,Yn}，
并且Xi与Xj(1≤i,j≤m)之间， Ys与Yt(1≤s,t≤m)之间没有边连接，
则G称为二部图。

 

　　　　　　　　完美（完备）匹配

 

对于一个图G与给定的一个匹配M，如果图G中不存在M的未
盖点(不饱和点)，则称匹配M为图G的完美匹配 。

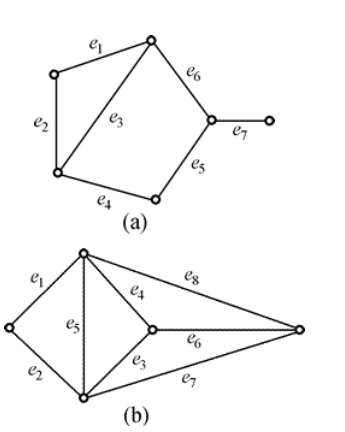
　　图(a)中, M = { e1, e4, e7 }为完美匹配(最大匹配),
它也是最小边覆盖。
　　图(b)中不可能有完美匹配, 因此, 对任何匹配都
存在未盖点。

 

　　任取一个最大匹配, 比如: M = { e2, e4 }, 则
M∪{ e6 }, M∪{ e8 }, M∪{ e7 }都是图的最小边覆盖。
　　任取一个最小边覆盖, 比如: W = { e1, e3, e6 }, 从
中移去一条相邻的边, 则{ e1, e3 }和{ e1, e6 }都是图的
最大匹配。
　　我们通常这样来做:

　　用最大匹配通过增加关联未盖点(不饱和点)的边获得最小边覆盖;
　  用最小边覆盖通过移去相邻的一条边获得最大匹配。

 

　　　　　　二分图的最大匹配

求二部图的最大匹配的算法有：
1. 网络流
　　1. 其中dinic为 O(Msqrt(N))
2. 匈牙利算法
　　1. O(MN)
　　2. 代码量最小，要求掌握
3. Hopcroft-Karp算法(匈牙利算法的改进)
　　1. O(Msqrt(N))

 

---

如果你不开心，那我就把右边这个帅傻子分享给你吧，
你看，他这么好看，跟个zz一样看着你，你还伤心吗？
真的！这照片盯上他五秒钟就想笑了。
一切都会过去的。
时间时间会给你答案2333