JZOJ5410. 小型耀斑

题目大意

某人放了\(q\)颗大伊万, 每一颗核弹的当量为\(k\).
在一个\(n*m\)的矩形中, 每一个地区都有其价值\(a_{i,j}\).
其中, 与爆炸中心\((x,y)\)曼哈顿距离小于\(k\)的每一个点都会受到波及, 损失为\((k-dis)*a_{i,j}\).
定义一个核弹的损失为它波及到的所有点的损失和. 求每一个核弹的损失.

解题思路

先放一个可能会有用的图:

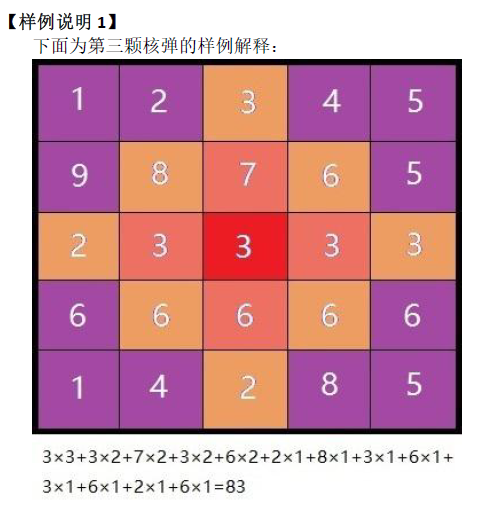
图中每一个格点的值是这个点的价值, 这个核弹的当量是\(3\), 爆炸中心是\((3,3)\).

考虑一个其实我们要求的其实是一个菱形. 然而菱形十分的不好处理, 于是可以考虑把原本的矩形转成菱形, 那么菱形就变成矩形啦!(
对于样例(上面的图)其实就是转成了这样一个东西:

所以.. 这个大伊万实际上造成的损失是:

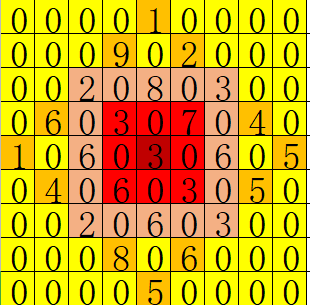
于是就可以用二位前缀和做到\(O(Qk)\)
不太行啊, 这个东西怎么优化呢? 考虑一颗核弹那些点的前缀和被加上, 哪些点被减去:

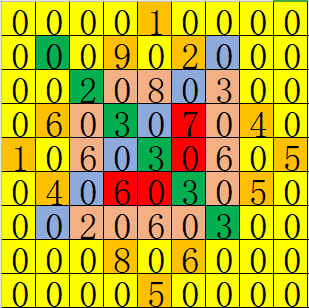
其中绿色的方格是加上的, 蓝色的方格是减去的. 这就可以用二次前缀和做到\(O(Q)\)了.

后记

这种题啊, 很考思维能力.. 有些同学用奇技淫巧也过了.. 所以看到菱形就要想想能不能转成矩形去做.

#include <cstdio>
#include <cstring>
#define N 2010
#define ll long long
#define init(a, b) memset(a, b, sizeof(a))
#define fo(i, a, b) for(int i = (a); i <= (b); ++i)
#define fd(i, a, b) for(int i = (a); i >= (b); --i)
using namespace std;
inline int read()
{
	int x = 0; char ch = getchar();
	while(ch < '0' || ch > '9')	ch = getchar();
	while(ch >= '0' && ch <= '9')	x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
	return x;
}
inline void write(ll x){if(!x)	return; if(x < 0)	putchar('-'), x = -x; write(x / 10); putchar('0' + x % 10);}
int n, m, k, a[N << 1][N << 1], pos[N][N][2];
ll sum1[N << 1][N << 1], sum2[N << 1][N << 1], sum3[N << 1][N << 1];
int main()
{
	freopen("flare.in", "r", stdin);
	freopen("flare.out", "w", stdout);
	n = read(), m = read(); k = n + m - 1;
	fo(i, 1, n)
	{
		int x = i, y = n - i + 1;
		fo(j, 1, m)	a[x][y] = read(), pos[i][j][0] = x++, pos[i][j][1] = y++;
	}
	fo(i, 1, k)	fo(j, 1, k)	sum1[i][j] = a[i][j] + sum1[i - 1][j] + sum1[i][j - 1] - sum1[i - 1][j - 1], sum2[i][j] = sum1[i][j] + sum2[i - 1][j - 1], sum3[i][j] = sum1[i][j] + sum3[i - 1][j + 1];
	for(int q = read(); q; --q)
	{
		int px = read(), py = read(), p = read(), x, y;
		x = pos[px][py][0], y = pos[px][py][1];
		printf("%lld\n", sum2[x + p - 1][y + p - 1] + sum3[x - p - 1][y + p] - sum2[x - p - 1][y - p - 1] - sum3[x + p - 1][y - p]);
	}
	return 0;
}

OJ评测机极其稳定, 交三次同样的代码就过了(