P5089 [eJOI2018]元素周期表

神奇的二分图连通块题。

题目大意

给定一张 \(n\) 行 \(m\) 列的矩阵，有 \(q\) 个元素 \((x_i,y_i)\) 为 \(1\)，其余均为 \(0\)。如果 \((x,y), (x,y'), (x',y)\) 上的元素均为 \(1\)，那么你可以将 \((x',y')\) 上的元素也扩展为 \(1\)。

求最少需要在初始矩阵中将几个 \(0\) 变成 \(1\)，才能使得整张矩阵能够通过上述规则的扩展使得所有元素均变为 \(1\)。\(m,n,q\le 2\times 10^5\)。

大体思路

这一类矩阵题目有一个套路的二分图建模方式：将 \(n\) 行作为 \(n\) 个左部点，编号 \(1\sim n\)；\(m\) 列作为 \(m\) 个右部点，编号 \(n+1\sim n+m\)。我们令所有 \((x,y)\) 上值为 \(1\) 的元素，在 \((x,y+n)\) 直接连边。题目要求的最终状态是每个位置的元素均为 \(1\)，即二分图构成完全二分图。

考虑题目中的扩展规则。\((x,y), (x,y'), (x',y)\) 上的元素均为 \(1\)，等价于 \((x,y), (x,y'), (x',y)\) 之间有连边，那么 \(x,y,x',y'\) 构成一个连通块。显然，添加了 \((x',y')\) 这条边后，连通块数量不会改变。假设原二分图有 \(C\) 个连通块，那么，无论每个连通块如何连边都不会使得 \(C\) 减少。为了使得 \(C\) 变为 \(1\)，需要额外连至少 \(C-1\) 条边（这是因为连通块变成完全二分图可能需要额外连边）。因此 \(ans\ge C-1\)。

接下来证明 \(ans =C-1\) 可行。考虑某一连通块中两个点 \(u,v\)。最终的目标是保证 \(u,v\) 之间连边。

• 如果 \((u,v)\in E\) 那么直接成立。
• 如果 \((u,v)\notin E\)，必然存在另外一个左部点 \(x\) 和右部点 \(y\)，使得 \((u,y),(x,v)\in E\)，并且存在 \(y\to x\) 的路径，如下图所示。

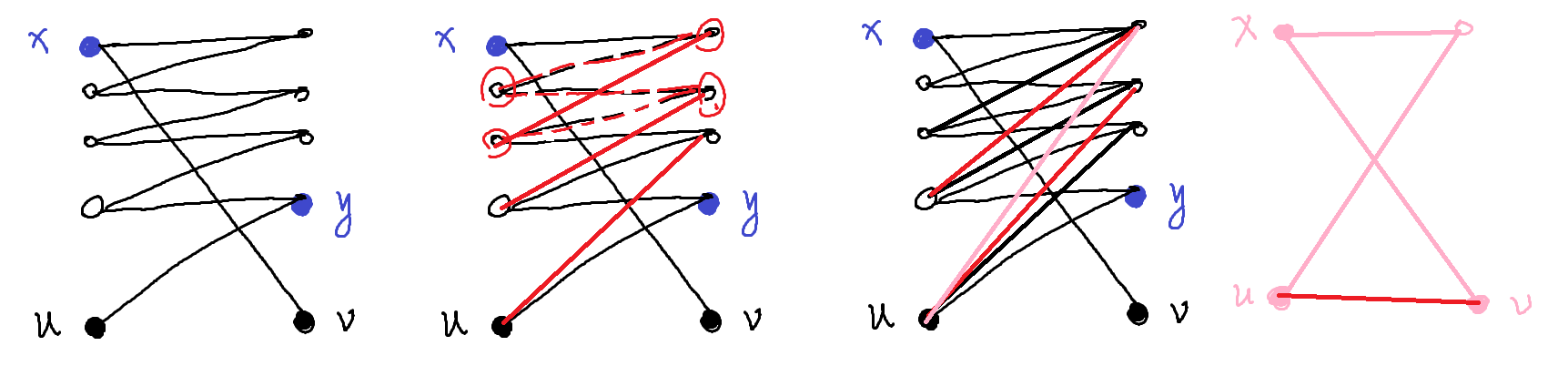
由于 Z 字形和 又 字行都是满足扩展条件的，可以在 \(y\to x\) 路径上将 Z 字形反复连边，最后会形成一个大的 又 字形，然后 \(u,v\) 便可连边。这证明了同一个连通块内任意两点之间都可以通过扩展自动连边，因此只需要额外连接 \(C-1\) 条边即可。

完整代码

#include <bits/stdc++.h>
using namespace std;
#define rep(ii,aa,bb) for(re int ii = aa; ii <= bb; ii++)
#define Rep(ii,aa,bb) for(re int ii = aa; ii >= bb; ii--)
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
typedef pair<int, int> PII;
const int maxn = 4e5 + 5;
namespace IO_ReadWrite {
	#define re register
	#define gg (p1 == p2 && (p2 = (p1 = _buf) + fread(_buf, 1, 1<<21, stdin), p1 == p2) ? EOF :*p1++)
	char _buf[1<<21], *p1 = _buf, *p2 = _buf;
	template <typename T>
	inline void read(T &x){
		x = 0; re T f=1; re char c = gg;
		while(c > 57 || c < 48){if(c == '-') f = -1;c = gg;}
		while(c >= 48 &&c <= 57){x = (x<<1) + (x<<3) + (c^48);c = gg;}
		x *= f;return;
	}
	inline void ReadChar(char &c){
		c = gg;
		while(!isalpha(c)) c = gg;
	}
	template <typename T>
	inline void write(T x){
		if(x < 0) putchar('-'), x = -x;
		if(x > 9) write(x/10);
		putchar('0' + x % 10);
	}
	template <typename T>
	inline void writeln(T x){write(x); putchar('\n');}
}
using namespace IO_ReadWrite;
int hd[maxn], ver[maxn], nxt[maxn], tot, n, m, q, ans;
inline void add(int u, int v) {
	ver[++tot] = v; nxt[tot] = hd[u]; hd[u] = tot;
	ver[++tot] = u; nxt[tot] = hd[v]; hd[v] = tot;
}
bool vis[maxn];
inline void dfs(int u) {
	for(int i = hd[u]; i; i = nxt[i]) {
		int v = ver[i];
		if(vis[v]) continue;
		vis[v] = 1;
		dfs(v);
	}
}
int main () {
	read(n); read(m); read(q);
	rep(i, 1, q) {
		int x, y;
		read(x); read(y);
		add(x, y + n);
	}
	rep(u, 1, n + m) if(!vis[u]) {
		vis[u] = 1;
		ans ++;
		dfs(u);
	}
	writeln(ans - 1);
	return 0;
}