SHOI2008 汉诺塔

暗藏玄机的线性 DP 题。不得不说 \(8002\) 年的 SHOI 题都比今天省选 Day1 好。

题目大意

汉诺塔由三根柱子（分别用 \(A\)、\(B\)、\(C\) 表示）和 \(n\) 个大小互不相同的空心盘子组成。一开始 \(n\) 个盘子都摞在柱子 \(A\) 上，大的在下面，小的在上面，形成了一个塔状的锥形体。

对汉诺塔的一次合法的操作是指：从一根柱子的最上层拿一个盘子放到另一根柱子的最上层，同时要保证被移动的盘子一定放在比它更大的盘子上面（如果移动到空柱子上就不需要满足这个要求）。我们可以用两个字母来描述一次操作：第一个字母代表起始柱子，第二个字母代表目标柱子。例如，AB 就是把柱子 \(A\) 最上面的那个盘子移到柱子 \(B\) 。汉诺塔的游戏目标是将所有的盘子从柱子 \(A\) 移动到柱子 \(B\) 或柱子 \(C\) 上面。

有一种非常简洁而经典的策略可以帮助我们完成这个游戏。首先，在任何操作执行之前，我们以任意的次序为六种操作（AB、AC、BA、BC、CA 和 CB）赋予不同的优先级，然后，我们总是选择符合以下两个条件的操作来移动盘子，直到所有的盘子都从柱子A移动到另一根柱子：

1. 这种操作是所有合法操作中优先级最高的；
2. 这种操作所要移动的盘子不是上一次操作所移动的那个盘子。

可以证明，上述策略一定能完成汉诺塔游戏。现在你的任务就是假设给定了每种操作的优先级，计算按照上述策略操作汉诺塔移动所需要的步骤数。

大体思路

有一个显然的事情：假设操作 AB 的优先级高于 AC，且当前所有圆盘都在 \(A\) 柱子，那么一定只会执行 AB 操作。

因此，我们使用动态规划解决，由于本题的操作步数与柱子编号有关，定义 \(f[i,x]\) 表示将 \(i\) 个柱子从 \(x\) 移走的步数，其中 \(x=1,2,3\) 分别对应 \(A,B,C\) 三根柱子。同时，我们需要根据优先级的强制规定记录这些圆盘被移去的柱子编号，即用 \(g[i,x]\) 表示将 \(i\) 个柱子从 \(x\) 移动到哪根柱子。

我们考虑状态如何转移。

根据普通汉诺塔，状态转移的思路是先将 \(i-1\) 个柱子移走，再将最大的第 \(i\) 个柱子移走。本题由于对操作有限制，假设前 \(i-1\) 块被移去的柱子编号为 \(y=g[i-1,x]\)，除了 \(x,y\) 之外第三根柱子编号 \(z=6-x-y\)。

将 \(i-1\) 块移到 \(y\) 后，如果 \(g[i-1,y]=z\)，相当于这 \(i-1\) 块接下来会被移到 \(z\)。那么，我们将 \(x\) 上的第 \(i\) 块移到 \(z\)，再将 \(i-1\) 块从 \(y\to z\)。因此，有

\[f[i,x]=f[i-1,x]+1+f[i-1,y],\ \ \ \ \ g[i,x]=z \]

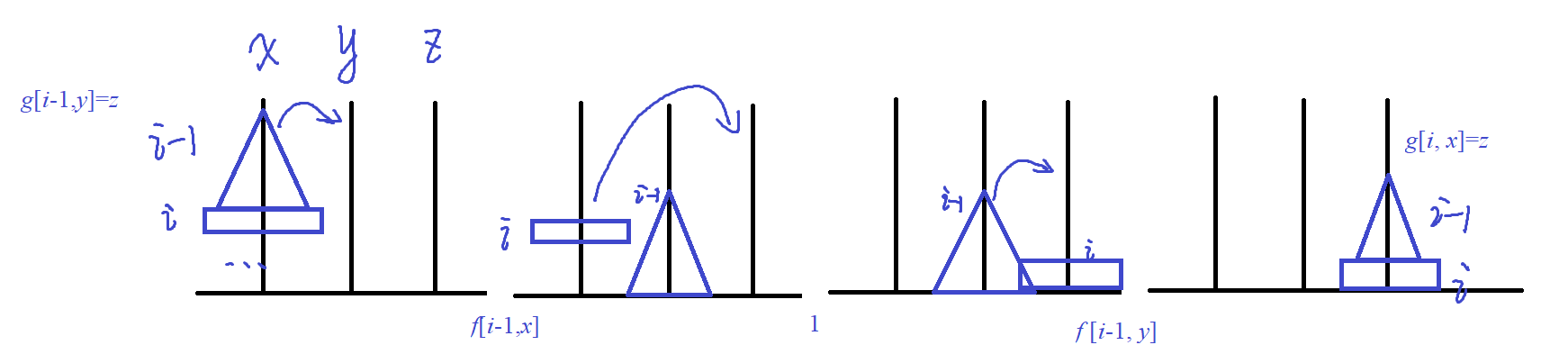
如果 \(g[i-1,y]=x\)，我们的目标是将 \(i\) 块移到 \(y\)。可以先将 \(i-1\) 块从 \(x\to y\)，将第 \(i\) 块从 \(x\to z\)，然后 \(i-1\) 块被从 \(y\to x\)，将第 \(i\) 块从 \(z\to y\)，最后将 \(i-1\) 块从 \(x\to y\)。因此，有

\[f[i,x]=f[i-1,x]+1+f[i-1,y]+1+f[i-1,x],\ \ \ g[i,x]=y \]

这样时间复杂度 \(O(n)\)，记得开 long long。

完整代码

#include <bits/stdc++.h>
using namespace std;
#define rep(ii,aa,bb) for(re int ii = aa; ii <= bb; ii++)
#define Rep(ii,aa,bb) for(re int ii = aa; ii >= bb; ii--)
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
typedef pair<int, int> PII;
const int maxn = 35;
namespace IO_ReadWrite {
	#define re register
	#define gg (p1 == p2 && (p2 = (p1 = _buf) + fread(_buf, 1, 1<<21, stdin), p1 == p2) ? EOF :*p1++)
	char _buf[1<<21], *p1 = _buf, *p2 = _buf;
	template <typename T>
	inline void read(T &x){
		x = 0; re T f=1; re char c = gg;
		while(c > 57 || c < 48){if(c == '-') f = -1;c = gg;}
		while(c >= 48 &&c <= 57){x = (x<<1) + (x<<3) + (c^48);c = gg;}
		x *= f;return;
	}
	inline void ReadChar(char &c){
		c = gg;
		while(!isalpha(c)) c = gg;
	}
	template <typename T>
	inline void write(T x){
		if(x < 0) putchar('-'), x = -x;
		if(x > 9) write(x/10);
		putchar('0' + x % 10);
	}
	template <typename T>
	inline void writeln(T x){write(x); putchar('\n');}
}
using namespace IO_ReadWrite;
ll n, f[maxn][4], g[maxn][4];
bool vis[4];
int main () {
	read(n);
	rep(t, 1, 6) {
		char U, V;
		ReadChar(U); ReadChar(V);
		int u = U - 'A' + 1, v = V - 'A' + 1;
		if(vis[u]) continue;
		vis[u] = 1;
		f[1][u] = 1, g[1][u] = v;
	}
	rep(i, 2, n)
		rep(x, 1, 3) {
			int y = g[i - 1][x];
			int z = 6 - x - y;
			if(g[i - 1][y] == z) {
				f[i][x] = f[i - 1][x] + 1 + f[i - 1][y];
				g[i][x] = z;
			} else {
				f[i][x] = f[i - 1][x] + 1 + f[i - 1][y] + 1 + f[i - 1][x];
				g[i][x] = y;
			}
		}
	writeln(f[n][1]);
	return 0;
}