【刷题记录】CF 交互构造题

CF 1779 E

给一张竞赛图，问一个 \(n-1\) 场淘汰赛之后可能的冠军有哪些。

通过交互得到竞赛图的度。然后运用竞赛图的一些性质：

1. 可能的冠军 \(u\) 能够到达其他所有节点；

2. \(1\) 的推论，所有可能的冠军节点构成强连通分量；

3. 竞赛图缩点后拓扑序唯一（即呈链状）；

4. 将入度从小到大排序后，若前 \(m\) 个点的入度之和为 \(\dfrac{m(m-1)}{2}\)，则这 \(m\) 个点构成第一个 SCC。

然后就结束了。

CF 1765 G

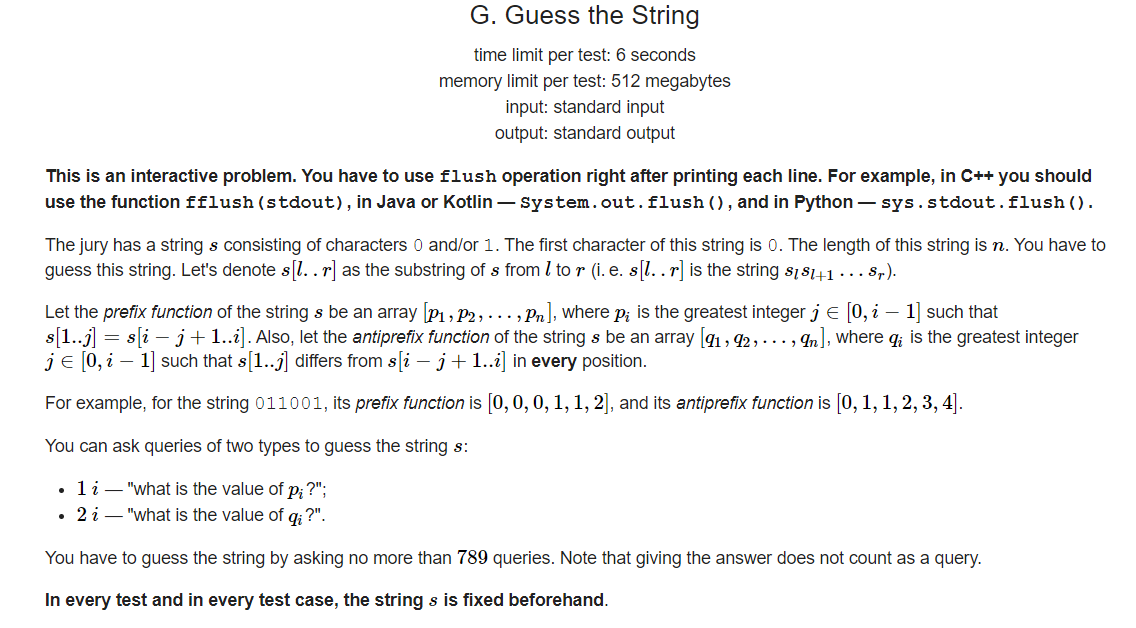
如果直接暴力，只询问 \(p_i\) 或 \(q_i\)，大概需要 \(n-1\) 次。

发现题目限制的 \(789\) 和 \(1000\) 差不了多少，因此一次确定两个元素即可。

假设 \(1\sim s_{i-2}\) 均已经确定。

如果询问的是 \(p_i\)，

• \(p_i \ge 2\) 时，\(s[1\sim 2]=s[i-1\sim i]\)；

• \(p_i=1\) 时，如果 \(s_2=0\)，那么说明后两位是 \(10\)，但 \(s_2=1\) 时后两位 \(00\) 或 \(10\) 无法确认；

• \(p_i=0\) 时，如果 \(s_2=1\)，则后两位为 \(11\)，否则无法确认。

如果询问的是 \(q_i\)，

• \(q_i\ge 2\) 时，后两位与 \(s_1s_2\) 恰好相反；

• \(q_i=1\) 时，如果 \(s_2=0\) 说明后两位为 \(01\)，否则无法确认；

• \(q_i=0\) 时，如果 \(s_2=1\) 说明后两位为 \(00\)，否则无法确认。

然后题目标签之所以有 \(\texttt{probabilities}\)，就是说你可以每次随机问 \(p_i\ \text{or}\ q_i\)，这样平均每两个字符需要 \(1.5\) 次。

CF 1365 G

首先有一个很显然的 \(2\log\) 的做法。

这种交互题一看就是二进制分类，对于下标，我们询问所有第 \(i\) 位为 \(1,0\) 的下标的数的或和。

对于一个下标 \(i\)，如果第 \(p\) 位为 \(c=0,1\)，则将第 \(p\) 位为 \(\overline c=1,0\) 纳入贡献。可以证明这样就得出了所有 \(A_j[j\neq i]\) 的异或和。

这个咋优化呢？没见过。

我们对下标重新编号，使得不存在 \(i\subseteq j\)。这样只需要询问每一位是 \(1\) 的数的或和。

根据 Sperner Theorem，\(\dbinom {13} 6>1000\)，因此 \(13\) 位即可。次数为 \(13\)。