【刷题记录】Codechef 2500+ problems

TAEDITOR

题目描述

你需要维护一个字符串，支持插入字符串和查询子串。

大体思路

题解给的是 BIT，好好做难度大概有蓝~紫。

然而事实上，这题相当于维护一个序列，支持区间插入和区间查询。

这就是文艺平衡树的板子题。实现时使用 fhqTreap，区间插入的建树利用笛卡尔树性质可以 \(O(n)\) 实现，区间查询就是 split 之后中序遍历。

时间复杂度 \(O(n\log n)\)。

但这样代码其实很长。

对于字符串的题，我们要敢于暴力。于是我用 STL::string 直接暴力然后过了。

View Code 
int Q, x;
string s, op, str;
int main () {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> Q;
	while(Q --) {
		cin >> op >> x;
		if(op[0] == '+') {
			cin >> str;
			s.insert(x, str);
		} else {
			int len;
			cin >> len;
			cout << s.substr(x - 1, len) << "\n";
		}
	}
	
	return 0;
}

MEOW1234

题目描述

有一个 \(10^5\) 行和 \(10^5\) 列的网格（行列编号均为 \(1\) 到 \(10^5\)）。\(N\) 个不同的格子被标记了（编号为 \(1\) 到 \(N\)）。第 \(i\) 个被标记的格子是 \((x_i,y_i)\)。

一个格子的集合 \(\mathbb S\) 是合适的如果满足：

  • 所有被标记的格子都属于这个集合
  • 对于任意一对属于集合的格子 \(A,B\)，它们之间存在一条路径长度等于 \(|x_A-x_B|+|y_A-y_B|\)，且该路径只包含集合中的点。路径中每一对相邻的格子必须有共同的边。

你需要求出最小的合适的集合的大小以及个数。由于合适的集合的个数巨大，输出对 \(10^9+7\) 取模。

大体思路

记被标记的点为黑点。

首先你需要发现一个性质，就是每一行真正有用的其实就是最边上两个黑点。

证明如下图所示：

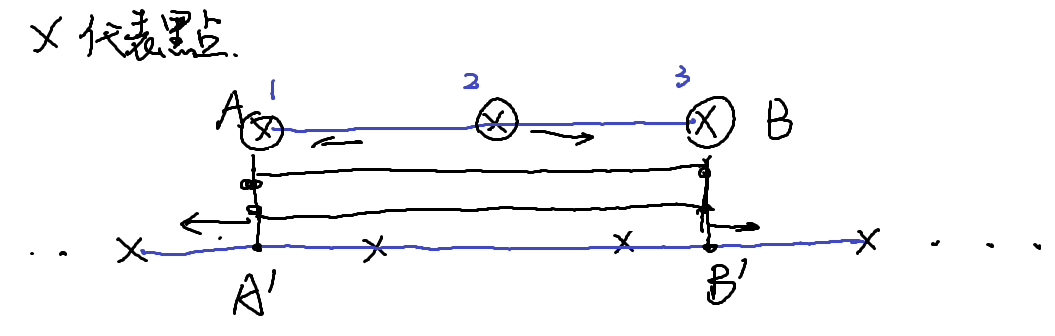
image

由于 \(A,B\in \mathbb S\)，线段 \(AB\) 必连。对于所有 \(B\) 右下方的点，\(AB\) 中间的点可以先水平向右到 \(B\)，再走 \(B\) 的路线即可。左侧同理。

对于正下方的部分，假设 \(A,B\) 被完全包含，\(AA',BB'\) 必连。线段 \(AA',BB'\) 上所有点 \(\in \mathbb S\)，故每两个对应点之间的水平线必连，因此整个矩形区域里所有点都要选，故 \(AB\) 中间点也必然会被满足。

然后我们存下来所有有黑点的行的 \([L,R]\) 表示最左，右出现的黑点的列号分别是 \(L,R\)。

下文的第 \(i\) 行指第 \(i\) 个有黑点的行。

假设当前考虑到第 \(i\) 行，那么该行点需要能够到达第 \(i+1\) 行及以后的最左，右点。故需要记录 \(L_i,R_i\) 的后缀最大值 \(suf_{i,L},suf_{i,R}\)。

然后我们根据当前行形成的线段 \([L,R]\) 和后面的最值 \([suf_{i+1,L},suf_{i+1,R}]\) 对应的线段的位置关系分成两大类。

一类是两个线段完全不相交，如下图所示。

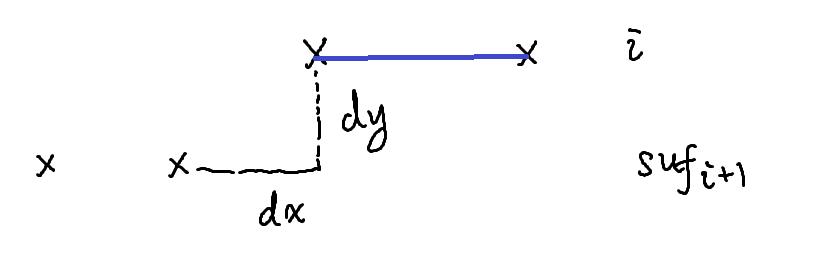
image

那么竖直方向一定连 \(dy-1\) 个点。至于方案数，从右上到左下一共需要 \(dx+dy\) 步，其中任意选出 \(dx\) 步水平，故为 \(\binom {dx+dy}{dx}\)。

另外一类是被包含，由上文的证明可得矩形区域内所有点都得选，同时方案只有一种。

View Code 
const ll mod = 1e9 + 7;
ll n, type;
ll fac[maxn], inv[maxn];
inline ll Pow(ll a, ll b) {
	ll res = 1;
	while(b) {
		if(b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res % mod;
}
inline void init(int N) {
	inv[0] = inv[1] = fac[0] = fac[1] = 1;
	rep(i, 2, N) fac[i] = 1ll * i * fac[i - 1] % mod;
	inv[N] = Pow(fac[N], mod - 2);
	Rep(i, N - 1, 2) inv[i] = 1ll * (i + 1) * inv[i + 1] % mod;
}
inline ll C(ll n, ll m) {
	if(m < 0 || m > n) return 0;
	if(m == n || m == 0) return 1;
	return fac[n] * inv[m] % mod * inv[n - m] % mod;
}
ll siz, cnt, nR;
struct node {
	int row, L, R;
} suf[maxn], cur;
vector <node> V;
map<int, set<int> > pts;

int main () {
	read(n); read(type);
	init(200000);
	rep(i, 1, n) {
		int x, y;
		read(x); read(y);
		pts[x].insert(y);
	}
	for(auto p : pts) {
		int pL = *(p.second.begin()), pR = *(p.second.rbegin());
		V.push_back({p.first, pL, pR});
		suf[nR ++] = {0, pL, pR};
	}
	Rep(i, nR - 2, 0) {
		suf[i].L = min(suf[i].L, suf[i + 1].L);
		suf[i].R = max(suf[i].R, suf[i + 1].R);
	}
	siz = 0, cnt = 1;
	cur = V[0];
	int Vsize = V.size();
	for(int i = 0; i < Vsize; i ++) {
		siz += cur.R - cur.L + 1;
		if(i == Vsize - 1) break;
		if(cur.R < suf[i + 1].L) {
			ll dx = suf[i + 1].L - cur.R, dy = V[i + 1].row - V[i].row;
			siz += dy - 1;
			cnt = cnt * C(dx + dy, dx) % mod;
			cur = {0, cur.R, V[i + 1].R};
		}
		else if(cur.L > suf[i + 1].R) {
			ll dx = cur.L - suf[i + 1].R, dy = V[i + 1].row - V[i].row;
			siz += dy - 1;
			cnt = cnt * C(dx + dy, dx) % mod;
			cur = {0, V[i + 1].L, cur.L};
		}
		else {
			ll dx = min(suf[i + 1].R, cur.R) - max(suf[i + 1].L, cur.L) + 1;
			ll dy = V[i + 1].row - V[i].row;
			siz = siz + dx * (dy - 1);
			cur = {0, min(max(suf[i + 1].L, cur.L), V[i + 1].L), max(min(suf[i + 1].R, cur.R), V[i + 1].R)};
		}
	}
	write(siz);
	if(type) putchar(' '), writeln(cnt);
	
	return 0;
}

ROBOTS

题目描述

Chefland 是⼀个很⼤的城市，在 2D 平⾯上包含了⽆数的路口。路口是如下的地⽅：

  • \((0,0)\) 和 \((1,0)\) 各有⼀个路口。
  • 每个路口和欧⽒距离为 \(1\) 的六个路口相连，并且六条边划分出了六个 \(60^{\circ}\) 的⻆。

下图描述了路口：

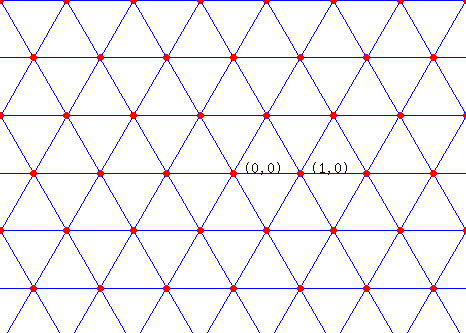
image

⼤厨制造了⼀个机器⼈，它可以在路口间来回穿梭。它⼀开始位于 \((0,0)\)，并朝向 \((1,0)\)。机器⼈接收到⼀串包含由 \(\{0,1,2,3,4,5\}\) 构成的字符串之后，会进⾏如下操作：

对于从左到右的每个数位 \(d\)， 机器⼈会逆时针旋转 \(60d\) 度，然后⾛到当前朝向的路⼝。⼤厨想测试机器⼈，所以他有⼀个⻓度为 \(N\) 的只包含 \(\{0,1,2,3,4,5\}\) 的字符串 \(S\)。他想执⾏ \(Q\) 次询问，每个询问包含 \(L\) 和 \(R\)，⼤厨会把机器⼈放在 \((0,0)\) 并⾯朝 \((1,0)\)，然后让机器⼈执⾏ \(S[L\dots R]\) 对应的操
作。请帮⼤厨计算机器⼈最终的位置。

\(1\le N,Q\le 2\cdot 10^5\)，误差要求小于 \(10^{-6}\)。

大体思路

这道题是到目前为止最简单的一道题了。

我们可以利用前缀和的思想，记录到第 \(i\) 步为止的位置 \(x_i,y_i\)，以及到第 \(i\) 步为止转过的 \(60^{\circ}\) 的个数 \(dir_i\)。那么，对于第 \(i\) 步，记 \(\vec{r_i} = (x_i,y_i)\)，有

\[dir_i=(dir_{i-1}+d_i) \bmod 6 \\ x_i=x_{i-1}+\cos(dir_i\cdot \dfrac \pi 3) \\ y_i=y_{i-1}+\sin(dir_i\cdot \dfrac \pi 3) \]

然后，询问 \(L\sim R\) 步的位移，那么显然 \(\vec r=\vec {r_R}-\vec{r_{L-1}}\)。

但是需要注意的是，此时得到的位移 \((x,y)\) 相当于从 \((0,0)\) 开始面朝逆时针 \(\alpha = dir_{L-1}\cdot \dfrac \pi 3\) 的方向。因此，最终输出答案时，需要顺时针转 \(\alpha\)，即逆时针转 \(\theta=2\pi-\alpha\)。

根据线性代数的公式，\((x,y)\) 逆时针转动 \(\theta\) 后，有

\[\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}\cos\theta & -\sin\theta\\\sin\theta & \cos\theta\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix} \]

输出得到的 \((x',y')\) 即可。时间复杂度 \(O(N)\)。

int T, n, q, dir[maxn];
char str[maxn];
typedef pair<db, db> PDD;
PDD a[maxn], sum[maxn];
const db pi = acos(-1.0);
int main () {
	scanf("%d", &T);
	while(T --) {
		scanf("%d%d%s", &n, &q, str + 1);
		rep(i, 1, n) {
			int k = (str[i] ^ 48);
			dir[i] = (dir[i - 1] + k) % 6; 
			a[i].first = cos(1.0 * dir[i] * pi / 3.0);
			a[i].second = sin(1.0 * dir[i] * pi / 3.0);
			sum[i].first = sum[i - 1].first + a[i].first;
			sum[i].second = sum[i - 1].second + a[i].second;
		}
		while(q --) {
			int l, r;
			scanf("%d%d", &l, &r);
			db x = sum[r].first - sum[l - 1].first;
			db y = sum[r].second - sum[l - 1].second;
			db theta = ((6 - dir[l - 1]) % 6) * 1.0 * pi / 3.0;
			printf("%.8lf %.8lf\n", x * cos(theta) - y * sin(theta), y * cos(theta) + x * sin(theta));
		}
	}
	return 0;
}

PRT

题目大意

现在你有⼀棵 \(N\) 个节点（编号为 \(1\sim N\)）的树和⻓度为 \(N\) 的整数序列 \(A_i\)。你可以选取任意⼀个 \(1\sim N\) 的排列 \(p\)。然后把节点 \(i\) 赋值为 \(A_{p_i}\)。

节点 \(u,v\) 之间的路径的利润为路径上所有点的权值之和（包括 \(u,v\)）。

我们现在只考虑某个叶⼦到另⼀个叶⼦之间的路径。请求出所有该种路径的利润之和的最⼤可能值是多少。因为答案⾮常⼤，请输出对 \(10^9+7\) 取模的结果。

大体思路

首先有一个很显然的贪心：假设所有两个叶子之间的路径经过点 \(u\) 的次数是 \(t_u\)，那么拥有较大的 \(t_u\) 的节点 \(u\) 应该搭配较大的权值。

证明很简单。假设最优组合中存在 \(w_u>w_v\)，\(t_u < t_v\)，那么交换 \(u,v\) 的权值之后，总的利润之和增加了 \(\Delta=t_uw_v+t_vw_u-t_uw_u-t_vw_v=(w_u-w_v)(t_v-t_u)>0\)，因此原先不是最优。

那么，我们只需要统计出每个点出现的次数即可。

假设一共有 \(nL\) 个叶子节点，以 \(u\) 为根的子树中有 \(l_u\) 个叶子节点，那么对于叶子节点，其次数 \(t_u=nL-1\)；对于非叶子节点，从其任意两个不同儿子为根的子树中选择两个叶子都会经过它本身，且选择任意一个 \(u\) 子树内的叶子和子树以外的叶子也都会经过本身，故有：

\[t_u=\sum_{i,j\in \text{son}(u)}l_i\cdot l_j+l_u(nL-l_u)=\dfrac{1}{2}\left((\sum_{i\in son(u)}l_i)^2-\sum_{i\in son(u)}l_i^2\right)+l_u(nL-l_u) \]

这样就可以 \(O(N)\) 完成求 \(t_u\)。总复杂度为 \(O(N \log N)\)，瓶颈在于排序。

然后你交了一发发现 WA 了，因为本题还有许多细节。

首先，所谓的叶子节点实际上指的是边缘节点，因此如果根节点只有一个儿子，也算作叶子。对策是我们可以先找到一个度数 \(\ge 2\) 的节点作为根节点。

然后你自信满满又交了一发，WA 了。

仔细想一想，一棵树一定会有度数 \(\ge 2\) 的节点吗？当 \(N\le 2\) 时显然是没有，而当 \(N\ge 3\) 时一定会有。因此对于 \(N=2\)，答案为 \(A_1+A_2\)；对于 \(N=1\)，答案为 \(0\)，因为无法选出两个不同的叶节点。

ll T, n, a[maxn], tim[maxn], num[maxn], nL;
bool isLeaf[maxn];
vector <int> G[maxn];
inline void dfs_leaf(int u, int fa) {
	if(G[u].size() == 1) {
		isLeaf[u] = 1;
		nL ++;
		num[u] = 1;
		return;
	}
	for(auto v : G[u]) {
		if(v == fa) continue;
		dfs_leaf(v, u);
		num[u] += num[v];
	}
}
inline void dfs_dp(int u, int fa) {
	if(isLeaf[u]) {
		tim[u] = nL - 1;
		return;
	}
	ll sum0 = 0, sum1 = 0;
	for(auto v : G[u]) {
		if(v == fa) continue;
		dfs_dp(v, u);
		sum0 += num[v];
		sum1 += num[v] * num[v];
	}
	tim[u] = (sum0 * sum0 - sum1) / 2 + num[u] * (nL - num[u]);
}
int id[maxn];
inline bool cmp(int i, int j) {
	return tim[i] < tim[j];
}
int main () {
	read(T);
	while(T --) {
		read(n);
		rep(i, 1, n) read(a[i]);
		sort(a + 1, a + n + 1);
		rep(i, 1, n) {
			G[i].clear();
			isLeaf[i] = tim[i] = num[i] = 0;
			id[i] = i;
		}
		nL = 0;
		rep(i, 1, n - 1) {
			int u, v;
			read(u); read(v);
			G[u].push_back(v);
			G[v].push_back(u);
		}
		if(n <= 2) {
			ll ans = 0;
			rep(i, 1, n) ans = (ans + a[i]) % mod;
			writeln(ans * (n != 1));
			continue;
		}
		int rt = 0;
		rep(i, 1, n) if(G[i].size() > 1) {
			rt = i;
			break;
		}
		dfs_leaf(rt, 0);
		dfs_dp(rt, 0);
		sort(id + 1, id + n + 1, cmp);
		ll ans = 0;
//		rep(i, 1, n) printf("%lld ", tim[i]);
		rep(i, 1, n) (ans += a[i] * (tim[id[i]] % mod) % mod) %= mod;
		writeln(ans);
	}
	
	return 0;
}

发表于 https://www.cnblogs.com/Mars-LG/p/17014286.html ，转载请注明出处。

可折叠代码段语法：

<details>
<summary>标题</summary>

//Your Code

</details>
posted @ 2022-12-30 10:38  Mars_Dingdang  阅读(83)  评论(0)    收藏  举报