排序算法
归并是把两个或两个以上有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的,然后把有序子序列合并为整体有序序列。

注意:在递归中必须传入(low, middle)和(middle+1, high),而快排的递归中可以是(low, middle - 1)和(middle+1, high)
递归实现:
public void merge(int[] arr) {
if (arr == null || arr.length == 0)
return;
int[] copy = new int[arr.length];
mergeSort(arr, copy, 0, arr.length - 1);
}
private void mergeSort(int[] arr, int[] copy, int low, int high) {
if (low == high)
return;
int mid = (low + high) / 2;
mergeSort(arr, copy, low, mid);
mergeSort(arr, copy, mid + 1, high);
int i = mid;
int j = high;
int locCopy = high;
while (i >= low && j > mid) {
if (arr[i] > arr[j])
copy[locCopy--] = arr[i--];
else
copy[locCopy--] = arr[j--];
}
while (i >= low) {
copy[locCopy--] = arr[i--];
}
while (j > mid) {
copy[locCopy--] = arr[j--];
}
for (int k = low; k <= high; k++) {
arr[k] = copy[k];
}
}
非递归实现:
public void mergeSort(int[] arr) {
int len = 1;
while (len < arr.length) {
for (int i = 0; i < arr.length; i += 2 *len) {
merge(arr, i, len);
}
len *= 2;
}
}
public void merge(int[] arr, int i, int len) {
int start = i;
int lenI = i + len;
int j = i + len;
int lenJ = j + len;
int[] temp = new int[len * 2];
int count = 0;
while (i < lenI && j < lenJ && j < arr.length) {
if (arr[i] <= arr[j]) {
temp[count++] = arr[i++];
} else {
temp[count++] = arr[j++];
}
}
while (i < lenI && i < arr.length) {
temp[count++] = arr[i++];
}
while (j < lenJ && j < arr.length) {
temp[count++] = arr[j++];
}
count = 0;
while (start < j && start < arr.length) {
arr[start++] = temp[count++];
}
}
2、冒泡排序
重复的走访过要排序的数组序列,一次比较两个元素,如果顺序错误就交换他们,越小的元素会经过交换慢慢浮到数列顶端
[57,68,59,52]-> [57,59,68,52]-> [57,59,52,68]-> [57,52,59,68]-> [52,57,59,68]
比较相邻的元素,如果第一个比第二个大,就交换两者。对每一对相邻元素做相同的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大。针对所有的元素重复以上的步骤,除了最后一个。持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较
public static void bubbleSort(int[] num) {
int temp = 0;
for (int i = 0; i < num.length - 1; i++) {
for (int j = 0; j < num.length - 1 - i; j++) {
if (num[j] > num[j + 1]) { // 交换两数位置
temp = num[j];
num[j] = num[j + 1];
num[j + 1] = temp;
}
}
}
}
3、快速排序
通过一趟排序把待排序记录分割成独立两部分,其中一部分比基准元素小,一部分大于等于基准元素,然后再用同样的方法递归地排序两部分
把第0个位置看作中轴。和最后一个比,如果最后一个数小:换,如果最后一个数大:不换。交换完后再和小的那端比,如果小的那端数字小:不换,如果小的那端数字大:换。循环往复。注意快排必须先从数组最右端开始检查!!!即while中的两个小while不能颠倒次序。快排在无序时效率最高,有序时效率低

public void quickSort(int[] num, int low, int high) {
if (low < high) {
int middle = getMiddle(num, low, high);// 将数组一分为二
quickSort(num, low, middle - 1); // 对低端排序
quickSort(num, middle + 1, high); // 对高端排序
}
}
public int getMiddle(int[] num, int low, int high) {
int temp = num[low]; // 数组第一个数作为中轴
while (low < high) {
while (low < high && num[high] >= temp) {
high--;
}
num[low] = num[high]; // 比中轴小的移动到低端
while (low < high && num[low] <= temp) {
low++;
}
num[high] = num[low]; // 比中轴大的移动到高端
}
num[low] = temp; //中轴记录到尾
return low; //返回中轴位置
}
快速排序通常被认为是在同数量级的排序方法中平均性能最好的。但如果初始序列有大量重复元素,快排反而蜕化成冒泡排序,为改进,通常选择三向切分法。即对于每次切分,从数组左边到右边遍历一次维护三个指针,其中lt指针使得num[0]-num[lt-1]都小于切分元素,gt指针使得num[gt]-num[N-1]都大于切分元素。I指针使得num[lt]-num[i]都等于切分元素, num[i]-num[gt]还没扫描,切分算法到i>gt为止。gt和lt中间的元素不用处理了。之后的递归只对[lo,lt-1]和[gt+1,hi]操作即可。

除了上面的三指针改进,还可以在选取基准元素时,取最左边,最右边,中间这三个位置的元素的中间值。
快排的非递归实现:getMiddle()不用变。借助stack实现

快排什么时候会恶化?
快排的的时间性能取决于快排的递归深度,可以用递归树来描述这个过程。

最优情况下,partition每次都划分的很均匀,如果排序n个关键字,递归树的深度就是log2n+1,即仅需要递归log2n次。最坏情况下,待排序的序列为正序或者逆序,每次划分只得到一个比上一次划分少一个记录的子序列,如果递归画出来,它就是一颗斜树,需要执行n-1次递归调用,最终时间复杂度为n^2。
4、选择排序
选出最小的一个数和第一个位置数交换,然后在剩下的数当中选出最小的与第二个位置数交换,循环到倒数第二个数和最后一个数比较为止

public void selectSort(int[] arr) {
int position = 0;
int temp = 0;
for (int i = 0; i < arr.length; i++) {
position = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[position]) {
position = j; // position记录最小数的索引
}
}
temp = arr[i];
arr[i] = arr[position];
arr[position] = temp;
}
}
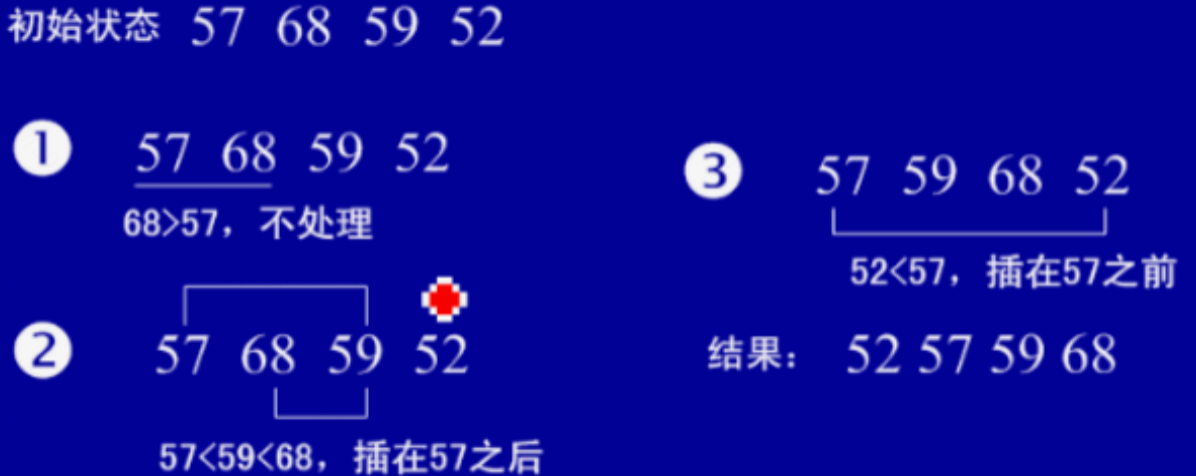
5、插入排序:
每一步把一个待排序的数字,按其大小插入到前面已经排序的序列的合适位置(从后向前找合适位置后),直到全部插入排序完为止

6、堆排序
堆排序和实现优先级队列都需要用到二叉堆。
堆的定义:最大堆:每个节点都小于等于父节点,堆顶元素是最大项,最小堆:每个节点都大于等于父节点,堆顶元素是最小项。初始时把要排序的数调整他们的存储顺序使之成为一个堆,这时堆的跟节点最大,此时构建堆完成。然后把根节点和堆的最后一个节点交换,对前面n-1个数重新调整使之成为堆,依次类推,直到只有两个节点的堆,并把他们交换,最后得到n个节点的有序序列。算法需要两个过程,一是堆的构建,二是实现排序过程。空间复杂度O(1),建堆复杂度O(n),调整堆的时间复杂度O(logn),调整堆的时间复杂度与堆的深度有关系,是lg2n的操作。所以插入删除节点的时间复杂度就是O(lg2n)

public static void heapSort(int[] arr) {
int len = arr.length;
for (int i = 0; i < len - 1; i++) {
buildHeap(arr, len - 1 - i); // 建堆,此时堆顶是最大元素
swap(arr, 0, len - 1 - i); // 把堆顶最大元素放到最下面
}
}
public static void buildHeap(int[] arr, int lastIndex) {
// 从最后一个节点的父节点开始,例如一共11个数,lastIndex是10,i从4开始
for (int i = (lastIndex - 1) / 2; i >= 0; i--) {
int k = i;
while (k * 2 + 1 <= lastIndex) { //如果当前k节点的子节点存在
int biggerIndex = k * 2 + 1; //biggerIndex是当前节点的左节点
if (biggerIndex < lastIndex) { // 如果小于lastIndex说明当前节点的左右节点都存在
if (arr[biggerIndex] < arr[biggerIndex + 1]) {
biggerIndex++; // 说明此时右节点的值较大,biggerIndex记录较大值
}
}
if (arr[k] < arr[biggerIndex]) {
swap(arr, k, biggerIndex); //如果k节点的值小于其较大子节点的值,就交换,让较大节点的值上浮
k = biggerIndex;
} else {
break;
}
}
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
首先是从最后一个非叶子节点开始,假设父节点下标是parent,左子节点就是2*parent+1,右子节点就是2*parent+2
算法复杂度:如果有递归调用。递归函数需要栈空间,而栈空间取决于递归的深度,比如深度遍历二叉树时,空间复杂度等价于二叉树的高度。
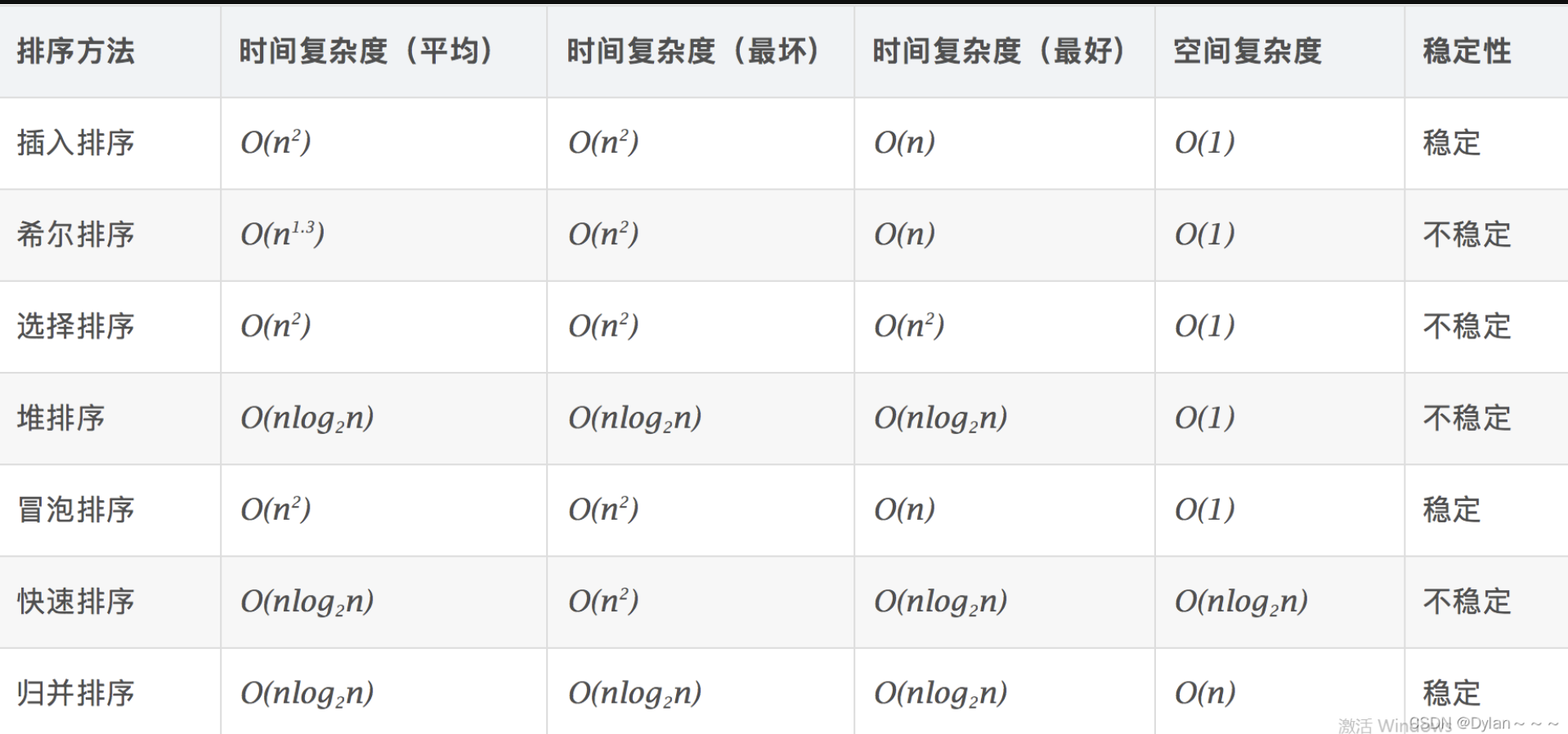
排序算法的稳定性概念:
稳定:如果a原本在b的前面,且a=b,排序后a仍然在b的前面。
不稳定:如果a原本在b的前面,且a=b,排序后a可能出现在b的后面。比如冒泡排序,如果把if条件改成,if(a[j]>=a[j+1]),则两个相等的数就会交换位置,变成不稳定的算法
不适合用链表的排序方法:快速排序,原因:
1)链表没有随机访问的能力,无法选择基准数
2)在链表中交换节点的代价比较高,且需要修改前驱节点的指向
3)数组中可以直接利用下标来访问元素,而链表只能从头开始遍历,找到所需要的元素
因此,对于链表来说,常用的排序算法有归并排序和插入排序。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号