VAE 推导

[[VAE]]

模型过程分析

这部分的信息摘录自变分自编码器（一）：原来是这么一回事

在整个VAE模型传播的过程中，我们并没有去使用 \(p(Z)\) (隐变量空间的分布) 是正态分布的假设，我们用的是假设 \(p(Z \mid X)\) (后验分布) 是正态分布。
具体来说, 给定一个真实样本 \(X_{k}\), 我们假设存在一个专属于 \(X_{k}\) 的分布 \(p\left(Z \mid X_{k}\right)\) (也叫做** 后验分布 ** ) 。同时我们进一步假设该分布是（独立的、多元的）正态分布。
为什么要强调“专属”呢? 因为我们后面要训练一个生成器 \(X=g(Z)\), 希望能够把从分布 \(p\left(Z \mid X_{k}\right)\) 采样出来的一个 \(Z_{k}\) 还原为 \(X_{k}\) 。如果假设 \(p(Z)\) 是正态分布, 然后从 \(p(Z)\) 中采样一个 \(Z\), 那么我们怎么知道这个 \(Z\) 对应于哪个真实的 \(X\) 呢? 现在 \(p\left(Z \mid X_{k}\right)\) 属于 \(X_{k}\) ，我们有理由说从这个分布采样出来的 \(Z\) 应该要还原到 \(X_{k}\) 中去。
事实上, 在论文《Auto-Encoding Variational Bayes》的应用部分, 也特别强调了这一点:

In this case, we can let the variational approximate posterior be a multivariate Gaussian with a diagonal covariance structure:

\[\log q_{\phi}\left(z \mid x^{(i)}\right)=\log \mathcal{N}\left(z ; \mu^{(i)}, \sigma^{2(i)} \boldsymbol{I}\right) \]

论文中的式子是实现整个模型的关键。
可到本文, 这时候每一个 \(X_{k}\) 都配上了一个专属的正态分布, 才方便后面的生成器做还原。但这样有多 少个 \(X\) 就有多少个正态分布了。我们知道正态分布有两组参数：均值 \(\mu\) 和方差 \(\sigma^{2}\) （多元的话, 它们都是向量）, 那我怎么找出专属于 \(X_{k}\) 的正态分布 \(p\left(Z \mid X_{k}\right)\) 的均值和方差呢? 好像并没有什么直接的思路。那好吧, 那我就用神经网络来拟合出来吧! 这就是神经网络时代的哲学：难算的我们都用神经网络来拟合, 在WGAN那里我们已经体验过一次了, 现在再次体验到了。
于是我们构建两个神经网络 \(\mu_{k}=f_{1}\left(X_{k}\right), \log \sigma_{k}^{2}=f_{2}\left(X_{k}\right)\) 来算它们了。我们选择拟合 \(\log \sigma_{k}^{2}\) 而不是直接拟合 \(\sigma_{k}^{2}\), 是因为 \(\sigma_{k}^{2}\) 总是非负的, 需要加激活函数处理, 而拟合 \(\log \sigma_{k}^{2}\) 不需要加激活函数, 因为它可正可负。到这里, 我能知道专属于 \(X_{k}\) 的均值和方差了, 也就知道它的正态分布长什么样了, 然后从 文个专属分布中采样一个 \(Z_{k}\) 出来, 然后经过一个生成器得到 \(\hat{X}_{k}=g\left(Z_{k}\right)\), 现在我们可以放心地最小 化 \(\mathcal{D}\left(\hat{X}_{k}, X_{k}\right)^{2}\), 因为 \(Z_{k}\) 是从专属 \(X_{k}\) 的分布中采样出来的, 这个生成器应该要把开始的 \(X_{k}\) 还原回来。 于是可以画出VAE的示意图。

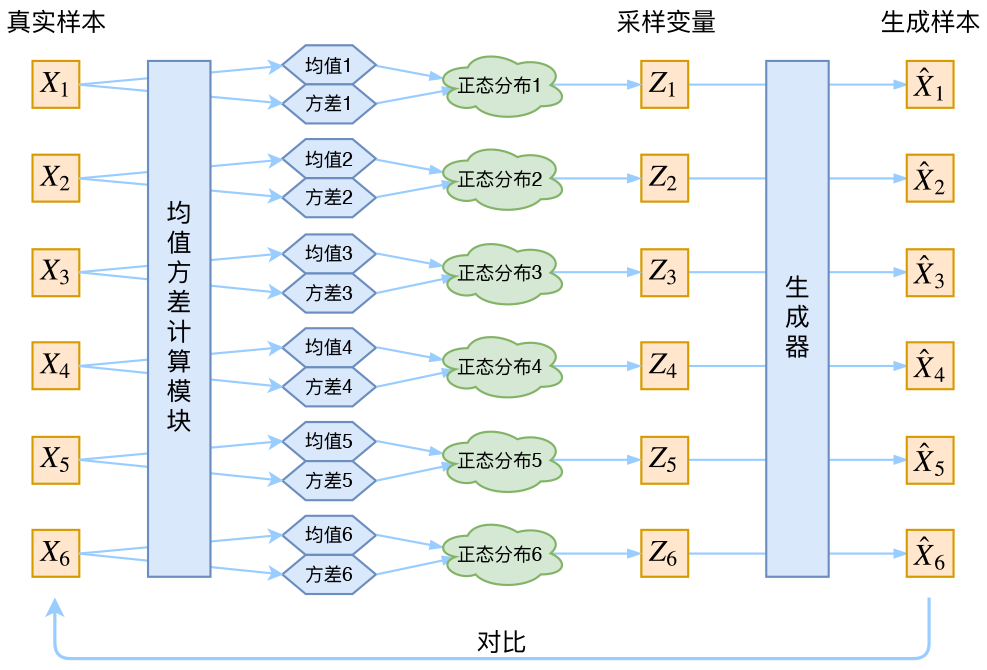
让我们来思考一下, 根据上图的训练过程, 最终会得到什么结果。
首先, 我们希望重构 \(X\), 也就是最小化 \(\mathcal{D}\left(\hat{X}_{k}, X_{k}\right)^{2}\), 但是这个重构过程受到噪声的影响, 因为 \(Z_{k}\) 是通 过重新采样过的, 不是直接由encoder算出来的。显然噪声会增加重构的难度, 不过好在这个噪声强 度（也就是方差）通过一个神经网络算出来的，所以最终模型为了重构得更好, 肯定会想尽办法让方 差为 \(\mathrm{0}\) 。而方差为 \(\mathrm{0}\) 的话, 也就没有随机性了, 所以不管怎么采样其实都只是得到确定的结果 (也就是 均值）, 只拟合一个当然比拟合多个要容易, 而均值是通过另外一个神经网络算出来的。说白了, 模型会慢慢退化成普通的AutoEncoder, 噪声不再起作用。这样不就白费力气了吗? 说好的生成模型呢?

别急, 其实 VAE还让所有的 \(p(Z \mid X)\) 都向标准正态分布看齐, 这样就防止了噪声为零, 同时保证了模型具有生成能力。怎么理解保证了生成能力呢? 如果所有的 \(p(Z \mid X)\) 都很接近标准正态分布 \(\mathcal{N}(0, I)\), 那么根据定义

\[p(Z)=\sum_{X} p(Z \mid X) p(X)=\sum_{X} \mathcal{N}(0, I) p(X)=\mathcal{N}(0, I) \sum_{X} p(X)=\mathcal{N}(0, I) \]

这样我们就能达到我们的先验假设： \(p(Z)\) 是标准正态分布。然后我们就可以放心地从 \(\mathcal{N}(0, I)\) 中采样来生成图像了。

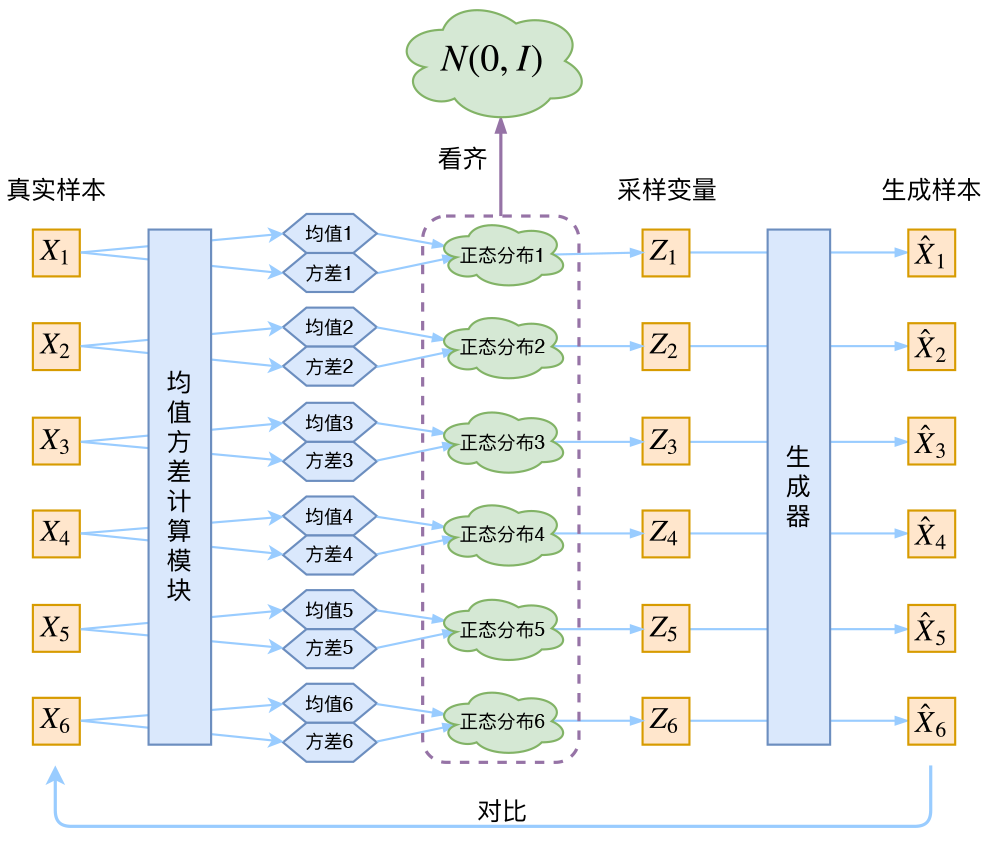
那怎么让所有的 \(p(Z \mid X)\) 都向 \(\mathcal{N}(0, I)\) 看齐呢? 如果没有外部知识的话, 其实最直接的方法应该是在重 构误差的基础上中加入额外的loss：

\[\mathcal{L}_{\mu}=\left\|f_{1}\left(X_{k}\right)\right\|^{2} \quad \text { 和 } \quad \mathcal{L}_{\sigma}^{2}=\left\|f_{2}\left(X_{k}\right)\right\|^{2} \]

因为它们分别代表了均值 \(\mu_{k}\) 和方差的对数 \(\log \sigma_{k}^{2}\), 达到 \(\mathcal{N}(0, I)\) 就是希望二者尽量接近于 0 了。不过, 这又会面临着这两个损失的比例要怎么选取的问题, 选取得不好, 生成的图像会比较模糊。所以, 原 论文直接算了一般（各分量独立的）正态分布与标准正态分布的 \(\mathrm{KL}\) 散度 \(K L\left(N\left(\mu, \sigma^{2}\right) \| N(0, I)\right)\) 作为 这个额外的loss, 计算结果为

\[\mathcal{L}_{\mu, \sigma^{2}}=\frac{1}{2} \sum_{i=1}^{d}\left(\mu_{(i)}^{2}+\sigma_{(i)}^{2}-\log \sigma_{(i)}^{2}-1\right) \]

这里的 \(d\) 是隐变量 \(Z\) 的维度, 而 \(\mu_{(i)}\) 和 \(\sigma_{(i)}^{2}\) 分别代表一般正态分布的均值向量和方差向量的第 \(i\) 个分量。 直接用这个式子做补充loss, 就不用考虑均值损失和方差损失的相对比例问题了。显然, 这个loss也 可以分两部分理解:

\[\begin{aligned} &\mathcal{L}_{\mu, \sigma^{2}}=\mathcal{L}_{\mu}+\mathcal{L}_{\sigma^{2}} \\ &\mathcal{L}_{\mu}=\frac{1}{2} \sum_{i=1}^{d} \mu_{(i)}^{2}=\frac{1}{2}\left\|f_{1}(X)\right\|^{2} \\ &\mathcal{L}_{\sigma^{2}}=\frac{1}{2} \sum_{i=1}^{d}\left(\sigma_{(i)}^{2}-\log \sigma_{(i)}^{2}-1\right) \end{aligned} \]

推导

由于我们考虑的是各分量独立的多元正态分布, 因此只需要推导一元正态分布的情形即可, 根据定义我 们可以写出

\[\begin{aligned} & K L\left(N\left(\mu, \sigma^{2}\right) \| N(0,1)\right) \\ =& \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-(x-\mu)^{2} / 2 \sigma^{2}}\left(\log \frac{e^{-(x-\mu)^{2} / 2 \sigma^{2} / \sqrt{2 \pi \sigma^{2}}}}{e^{-x^{2 / 2} / \sqrt{2 \pi}}}\right) d x \\ =& \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-(x-\mu)^{2} / 2 \sigma^{2}} \log \left\{\frac{1}{\sqrt{\sigma^{2}}} \exp \left\{\frac{1}{2}\left[x^{2}-(x-\mu)^{2} / \sigma^{2}\right]\right\}\right\} d x \\ =& \frac{1}{2} \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-(x-\mu)^{2} / 2 \sigma^{2}}\left[-\log \sigma^{2}+x^{2}-(x-\mu)^{2} / \sigma^{2}\right] d x \end{aligned} \]

整个结果分为三项积分, 第一项实际上就是 \(-\log \sigma^{2}\) 乘以概率密度的积分（也就是 1 )，所以结果是 \(-\log \sigma^{2}\); 第二项实际是正态分布的二阶矩, 熟悉正态分布的朋友应该都清楚正态分布的二阶矩为 \(\mu^{2}+\sigma^{2}\); 而根据定义, 第三项实际上就是“-方差除以方差 \(=-1\) ”。所以总结果就是

\[K L\left(N\left(\mu, \sigma^{2}\right) \| N(0,1)\right)=\frac{1}{2}\left(-\log \sigma^{2}+\mu^{2}+\sigma^{2}-1\right) \]