01_机器学习-数学基础(更新中...)

机器学习-数学基础

目录

• 机器学习-数学基础
  • 一、概述
  • 二、线性代数
    • 2.9 几种常用的距离
      • 5.余弦相似度
  • 三、概率
  • 四、信息论
  • 五、数值计算
  • 六、最优化
    • 6.7.阻尼牛顿法
    • 6.8.拟牛顿法

一、概述

二、线性代数

2.9 几种常用的距离

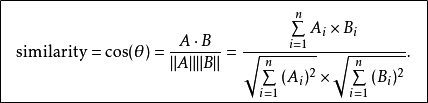
5.余弦相似度

• 0.基本解释：
  • 公式：
    • 
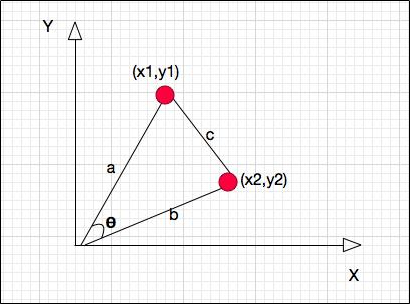
  • 几何解释：
    • 
• 1.解决问题：通过测量两个向量的夹角的余弦值来度量他们之间的相似性
• 2.取值：取值在[-1,1]之间
• 3.说明：两个向量的夹角的余弦值确定两个向量是否大致指向相同的方向
• 4.扩展：上下界对任何维度都适用，尤其是多维，用处更广
• 5.常用领域：
  • 文本挖掘中的文件比较
  • 数据挖掘中
• 6.python代码

# 2.9.5 夹角余弦

from numpy import *
vector1 = mat([1,2,3])
vector2 = mat([4,5,6]).T
print(dot(vector1,vector2)/(linalg.norm(vector1)*linalg.norm(vector2)))

# 输出结果：[[0.97463185]]

三、概率

四、信息论

五、数值计算

六、最优化

6.7.阻尼牛顿法

• 1.引入
  -
• 2.推导
  -

from linear_search.wolfe import *
from linear_search.Function import *
from numpy import *

# 阻尼牛顿法
def newton(f, start):
    fun = Function(f)
    x = array(start)
    g = fun.grad(x)
    while fun.norm(x) > 0.01:
        G = fun.hesse(x)
        d = (-dot(linalg.inv(G), g)).tolist()[0]
        alpha = wolfe(f, x, d)
        x = x + alpha * array(d)
        g = fun.grad(x)
    return x

6.8.拟牛顿法

• 1.概述：
  

• 2.推导
  

# coding=utf-8
from linear_search.wolfe import *
from linear_search.Function import *
from numpy import *


# 拟牛顿法
def simu_newton(f, start):
    n=size(start)
    fun = Function(f)
    x = array(start)
    g = fun.grad(x)
    B=eye(n)
    while fun.norm(x) > 0.01:
        d = (-dot(linalg.inv(B), g)).tolist()
        alpha = wolfe(f, x, d)
        x_d=array([alpha * array(d)])
        x = x + alpha * array(d)
        g_d=array([fun.grad(x)-g])
        g = fun.grad(x)
        B_d=dot(B,x_d.T)
        B=B+dot(g_d.T,g_d)/dot(g_d,x_d.T)-dot(B_d,B_d.T)/dot(x_d,B_d)
    return x