20200302——复习比赛+机器学习loss+KMP+AC自动机

罗兰

心情平和，不急不躁

1.目前102上

允许梯度回传，解决了很大正确性的问题，存储容器clear

2.复习比赛旧题

无论感觉多么想不起来，也要硬想。然后分析

想核心思路

3.机器学习——loss函数

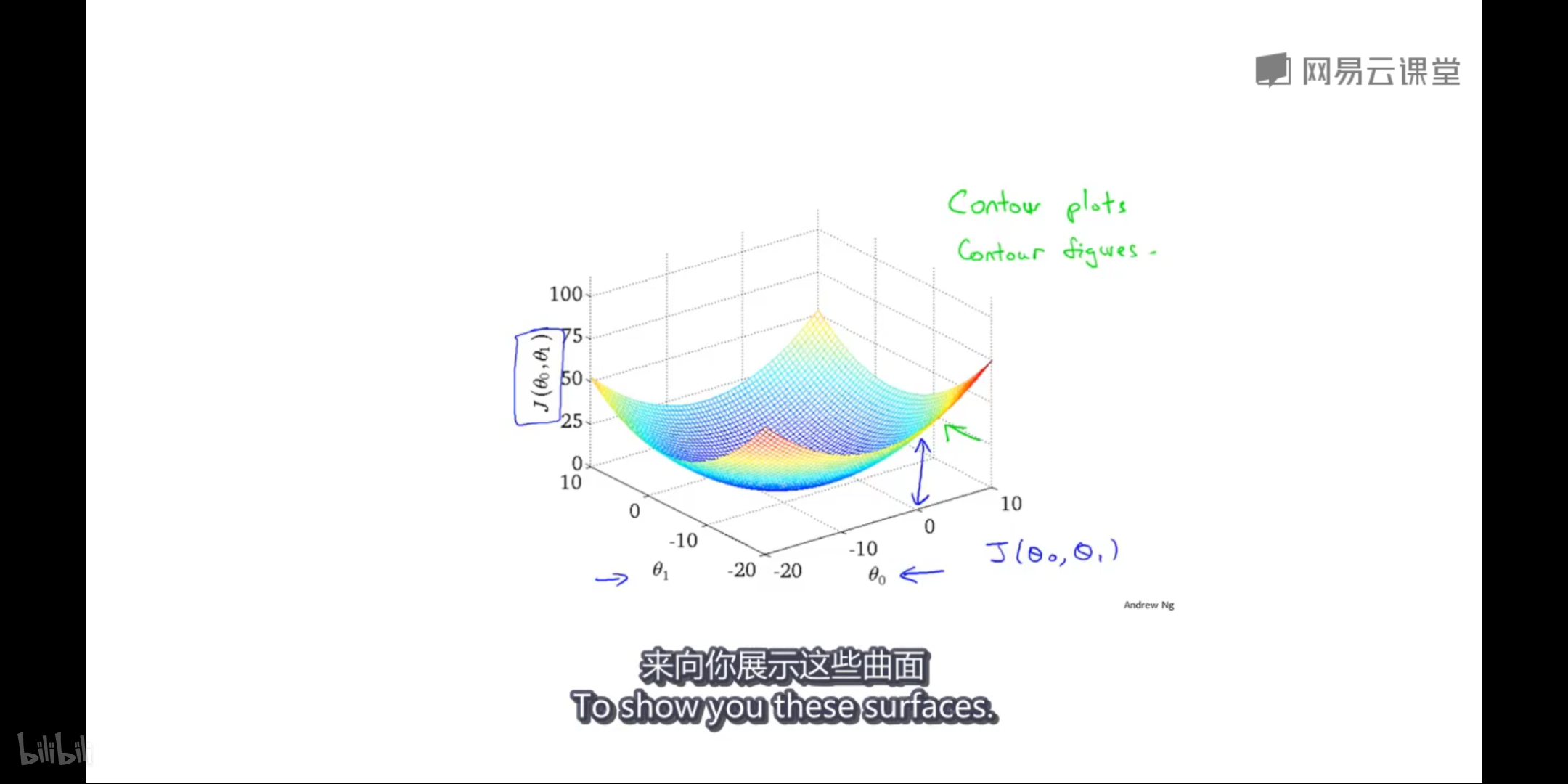
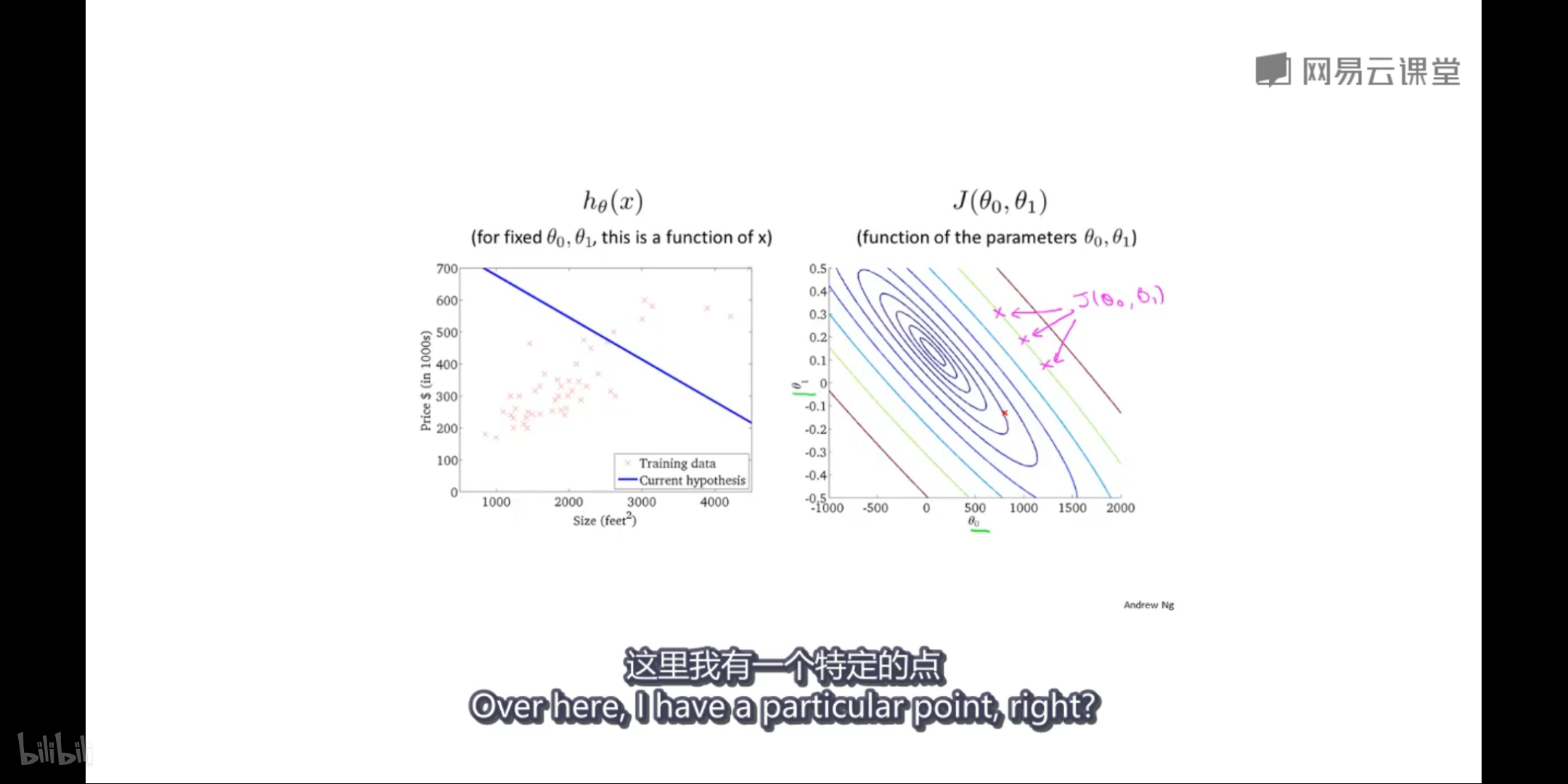
底部横纵坐标分别表示 01 02两个参数，表示在不同参数组合下损失函数的大小，多椭圆线汇合形成整体椭圆曲面。用等高线来表示相当于只看底面。希望找到椭圆曲面最底部的点，使得loss最小，即椭圆圆心的位置。过程中在等高线上的两个参数的不同数值组合，loss值都是相同的

 

 

 

 

 

4.KMP（单模式匹配）+AC自动机（多模式匹配）

后缀不包括自身

AC自动机两大要点：

tail指针，指向当前字符串的最大匹配后缀

visit记录是否是终点，字符串位数

ac自动机时间复杂度：
　　假设有N个模式串，平均长度为L；文章长度为M。 建立Trie树：O(N*L) 建立fail指针：O(N*L) 模式匹配：O(M*L) 所以，总时间复杂度为:O( (N+M)*L )。
　　在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。

 

 

#include<bits/stdc++.h>
using namespace std;
struct Trie{
    Trie *next[26],*fail;
    int cnt;
}*root;
struct status{
    Trie *last;
    int cnt;
    status(Trie *last,int cnt):last(last),cnt(cnt){}
};
Trie* newNode()
{
    Trie *pos=new Trie;
    memset(pos->next,0,sizeof(pos->next));
    pos->fail=0;
    pos->cnt=0;
    return pos;
}
void init(){root=newNode();}

void Insert(string str)
{
    Trie *pos=root;
    for(int i=0;i<str.size();++i)
    {
        int c=str[i]-'a';
        if(!pos->next[c])
        {
            pos->next[c]=newNode();
        }
        pos=pos->next[c];
    }
    pos->cnt++;
}
void getfail()
{
    queue<Trie*> Q;
    for(int i=0;i<26;++i)
    {
        if(root->next[i])
        {
            root->next[i]->fail=root;
            Q.push(root->next[i]);
        }
        else
            root->next[i]=root;
    }
    while(!Q.empty())
    {
        Trie *q=Q.front();Q.pop();
        for(int i=0;i<26;++i)
        {
            if(q->next[i])
            {
                q->next[i]->fail=q->fail->next[i];
                //q already in.so just push next part
                Q.push(q->next[i]);
            }
            else
            {
                //also not also connect
                q->next[i]=q->fail->next[i];
            }
        }
    }
}
int find(string str)
{
    Trie *pos=root,*last;
    queue<status> Q;
    int ans=0;
    for(int i=0;i<str.size();++i)
    {
        int c=str[i]-'a';
        if(pos->next[c])
        {
            pos=pos->next[c];
            last=pos;
            while(last->cnt)
            {
                ans+=last->cnt;
                Q.push(status(last,last->cnt));
                last->cnt=0;
                last=last->fail;
            }
        }

    }
    while(!Q.empty())
    {
        status q=Q.front();Q.pop();
        q.last->cnt=q.cnt;
    }
    return ans;

}
int main()
{
    ios::sync_with_stdio(false);
    freopen("a.in","r",stdin);
    int T,n;
    cin>>T;
    string tt;
    while(T--)
    {
        cin>>n;
        //each init update root == change tree,so each round update once
        init();
        for(int i=0;i<n;++i)
        {

            cin>>tt;
            Insert(tt);
        }
        getfail();
        cin>>tt;
        int ans=find(tt);
        cout<<ans<<endl;
    }
    return 0;
}