张三木教你学动态规划
动态规划
动态规划(Dynamic Programming)在算法里面算是比较困难的。但是,其实它和分治法非常相似:先求解子问题,然后通过子问题的解来得到原问题的解。
与分治法不同的是,动态规划的子问题往往不是独立的。在用分治法求解时,有些子问题的答案被大量的重复计算,如果我们可以把这些子问题的答案存起来,需要时再取出来用,这样就可以避免大量计算。动态规划就是利用了这一种思想。
动态规划的基本要素
最优子结构
当一个问题的最优解包含了其子问题的最优解,这个问题就具有最优子结构。
重叠子问题性质
在问题的求解过程中,很多子问题的解会被多次使用。
动态规划的设计步骤
- 找出最优解的性质,并且刻画其结构特征
- 递归地定义最优值
- 以自底向上的方式计算最优值
- 根据计算最优值时得到的信息,构造最优解
状态转移方程
在动态规划中,当前状态往往是上一阶段状态和上一阶段决策的结果,如果给定了第K阶段的状态Sk和决策uk(Sk),则第K+1阶段状态Sk+1也完全确定,则它们之间存在一种对应的数学关系。用函数来表示这种关系的方程,称为状态转移方程。
经典例题
数字三角形
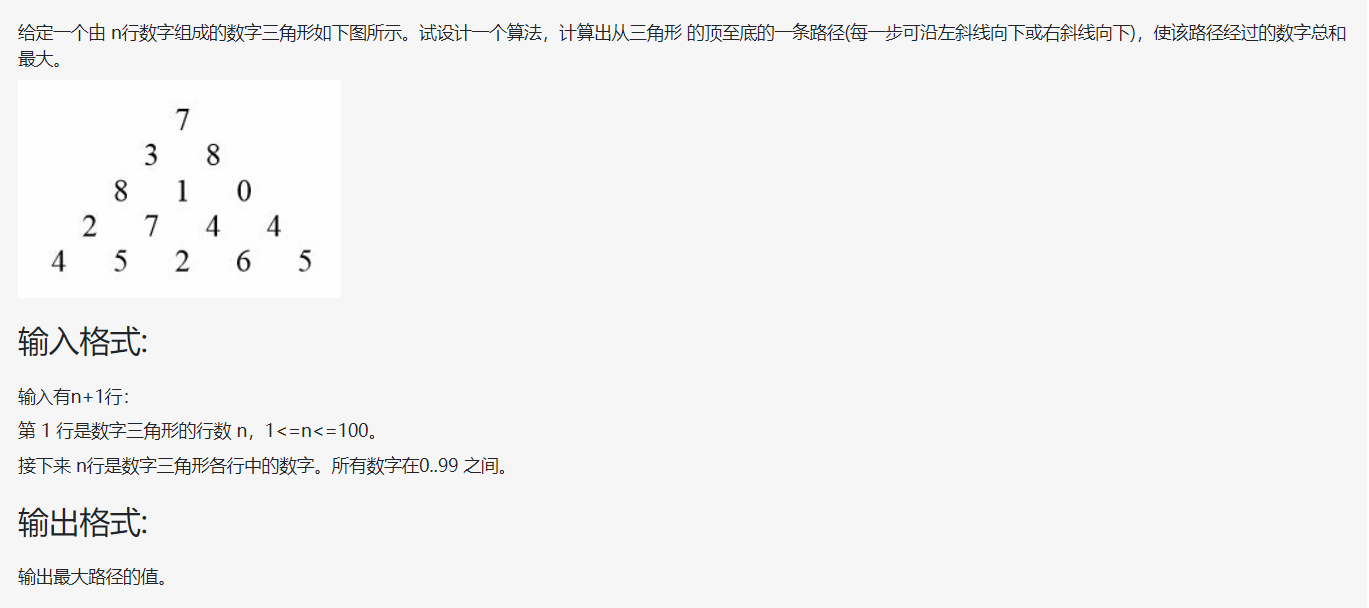
解析:
我们可以先用一个二维数组trangle[n][n]来存放该数字三角形:
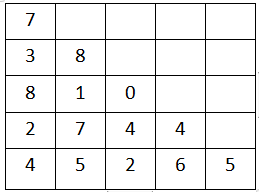
注:顶点坐标为(1,1)。
可见和最大的路径为:
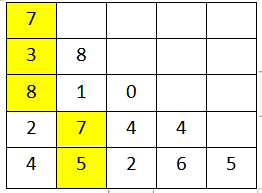
可以看出,设trangle[i][j]为到trangle[i][j]路径的最大和,必须求出trangle[i+1][j+1]和trangle[i+1][j]的值,再取两者中的较大值加上原来的trangle[i][j]的值。
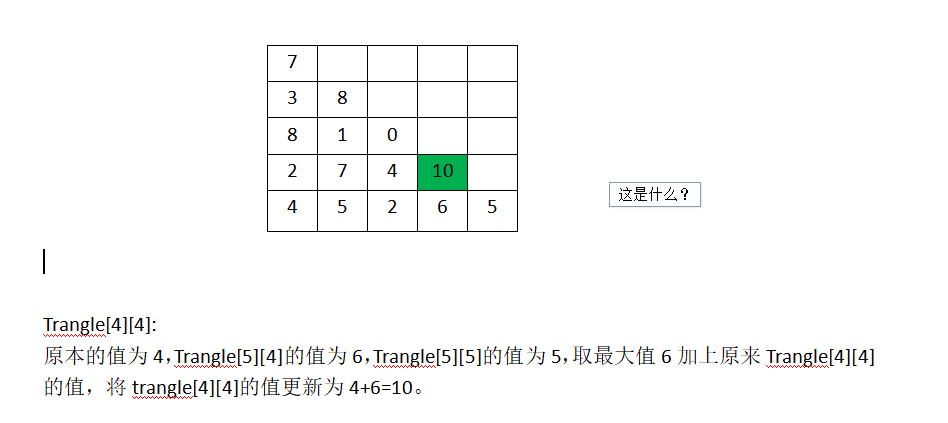
所以该题的状态转移方程为:
$$
trangle[i][j] =
\left {
\begin{aligned}
& trangle[i][j] & i=n \
& Max(trangle[i+1][j+1], trangle[i+1][j])+trangle[i][j]& i <n ,j<n \
\end{aligned}
\right .
$$
由此类推,可以用自底向上的方式填表:
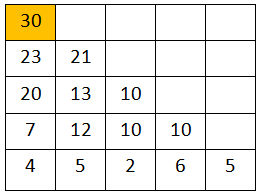
最上面的trangle[1][1]就是我们所求的路径和最大值。
具体代码实现:
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXLENGTH 105
int trangle[MAXLENGTH][MAXLENGTH];
//求出最大路径和的方程
void findMaxSum(int trangle[][MAXLENGTH], int n) {
for (int i = n; i > 0; i--) {
//自底向上填表
for(int j = 1; j <= i; j++) {
int temp = max(trangle[i + 1][j + 1], trangle[i + 1][j]);
trangle[i][j] = trangle[i][j] + temp;
}
}
}
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
cin >> trangle[i][j];
}
}
findMaxSum(trangle, n);
cout << trangle[1][1] << endl;
system("pause");
return 0;
}
单调递增子序列
题目如下:
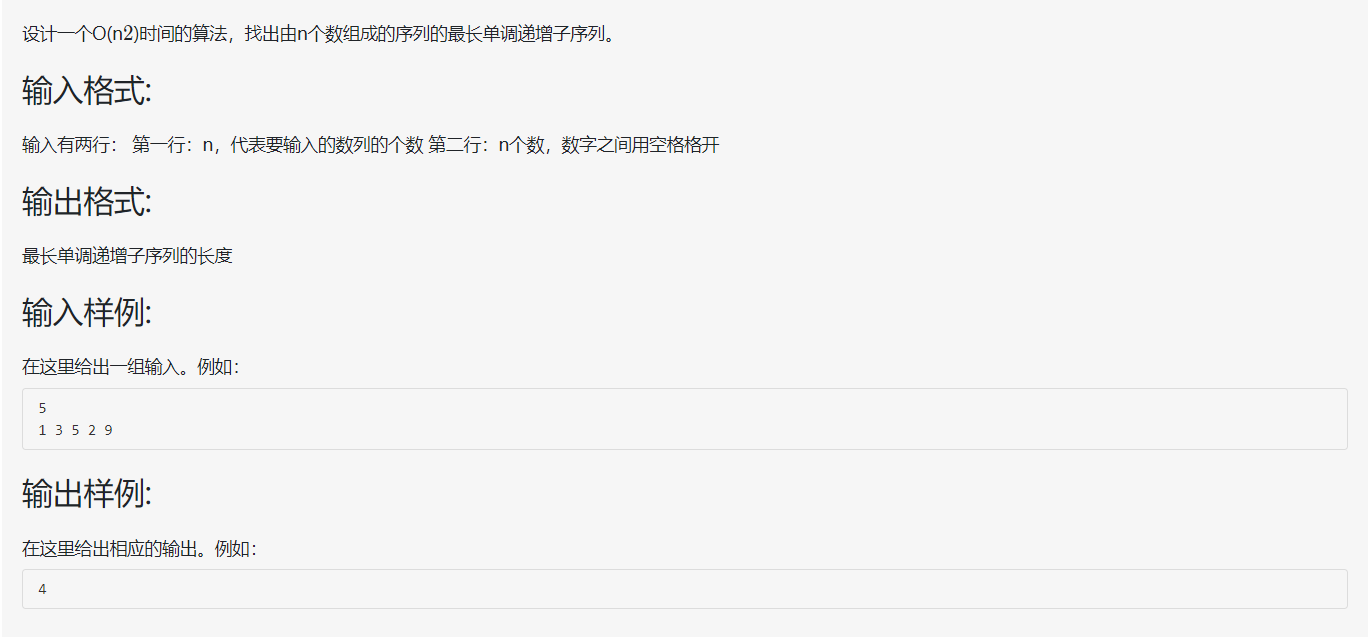
解析:
由样例我们可以看出,最长单调递增子序列为1 3 5 9,也就是说单调递增子序列不一定是连续的。
我们可以先用一个一维数组arr[n]来存放输入,再定义一个longestArr[n]数组,其中,longestArr[i]表示从开始到下标为i的元素的最长子序列的长度。可以进行两次循环,第一次循环(i)由第二个元素到最后一个元素,第二次循环由第一个元素到第i-1元素,判断外循环的longest[i]和内循环的longest[j]+1,取其中较大值。
由此我们可以知道,longest[i]依赖于longest[j],可以得到状态方程为:
$$
longest[i] =
\left {
\begin{aligned}
& 1 & i=1 \
& Max(longest[i],longest[j]+1)& i <n ,j<i \
\end{aligned}
\right .
$$
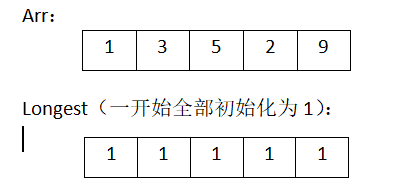

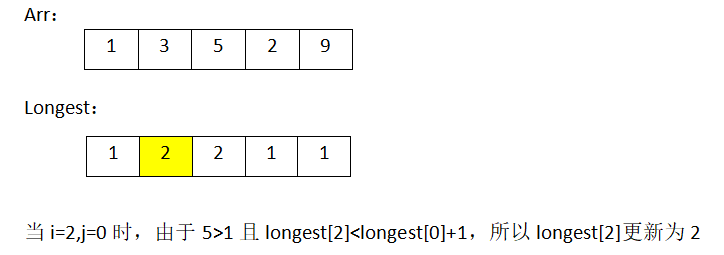

由此可一直类推,最后得到的longest为:
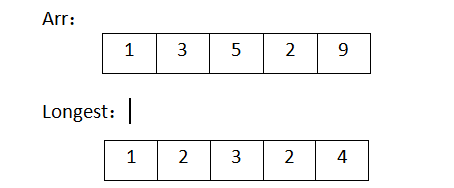
最遍历longest,得到的最大值即为我们所求的最长单调递增子序列的长度。
代码如下:
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXLENGTH 1000
int longestArr[MAXLENGTH];
int findLongest(int arr[],int n){
int maxNum = 0;
//外循环(从第二个元素到最后一个元素)
for (int i = 1; i < n; i++) {
//内循环(从第一个元素到外循环的前一个)
for (int j = 0; j < i; j++) {
if (arr[i] > arr[j]) {
// 取两者的最大值
longestArr[i] = max(longestArr[i], longestArr[j] + 1);
}
}
}
//遍历以取得最大值
for (int i = 0; i < n; i++) {
if (longestArr[i] > maxNum) {
maxNum = longestArr[i];
}
}
return maxNum;
}
int main() {
int arr[MAXLENGTH];
int n;
for (int i = 0; i < MAXLENGTH; i++) {
longestArr[i] = 1;
}
cin >> n;
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
int find = findLongest(arr, n);
cout << find << endl;
system("pause");
return 0;
}
租借游艇问题
题目如下:
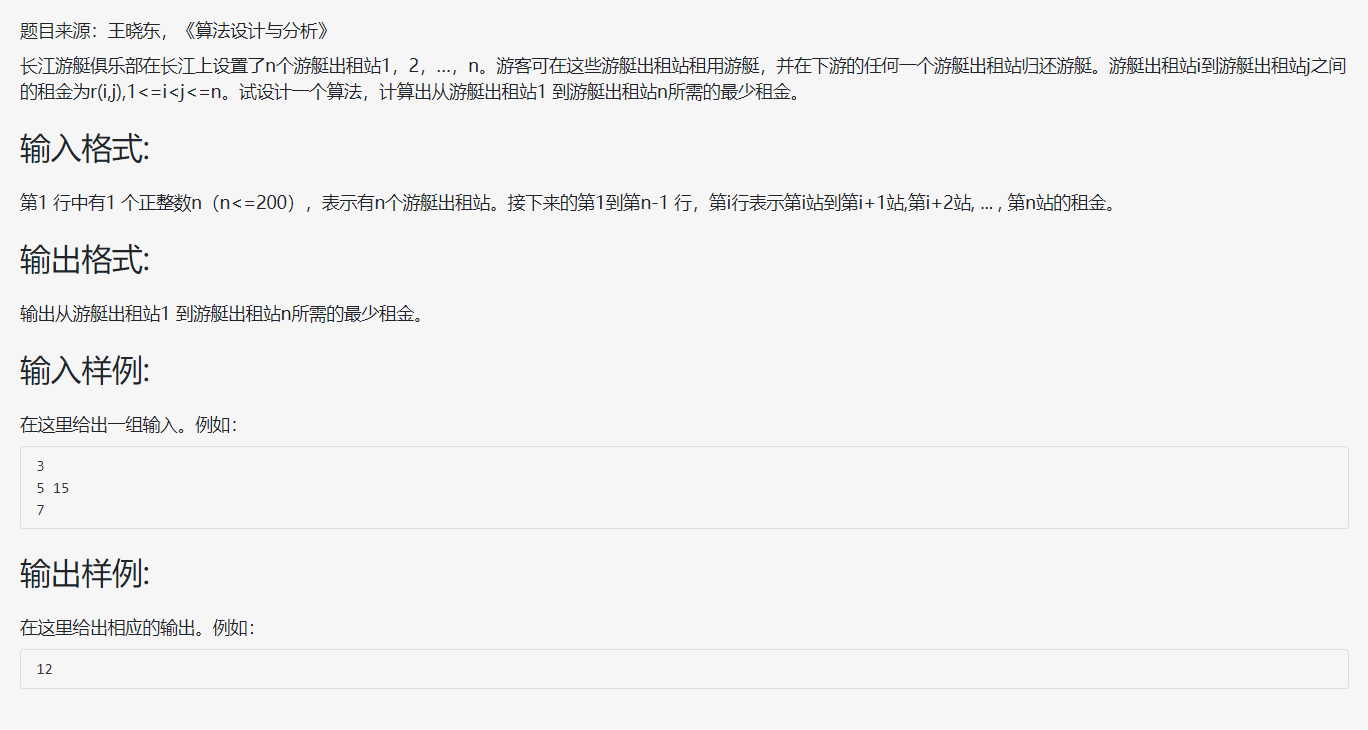
解析:
首先定义一个cost[n][n]数组,cost[i][j]表示从第i站到第j站租借所需要的最小费用(首先初始化为第i站到第j站租借所需要的费用 )。所以,最优的解决办法是:在i到j中,可以找到一个k,使得cost[i][k]+cost[k][j]小于cost[i][j]。 然后用cost[i][k]+cost[k][j]来代替cost[i][j]。
这样我们就得到了状态转移方程:
$$
cost[i][j] =
\left {
\begin{aligned}
& cost[i][j] & i=j \
& Min(cost[i][k]+cost[k][j],cost[i][j])& i<j \
\end{aligned}
\right .
$$
接着,我们可以从长度为2的距离开始找最优解,直到最后找到距离为n。
代码如下:
#include<iostream>
using namespace std;
#define MAXLENGTH 10000
double cost[MAXLENGTH][MAXLENGTH];
void findCheapest(double cost[][MAXLENGTH],int n) {
// 从距离为2的开始找(比如1->2就是距离为2)
for (int r = 2; r <= n; r++) {
for (int i = 1; i <= n-r+1; i++) {
//r(i,j)的长度为r
int j = r + i - 1;
for (int k = i; k <= j; k++) {
//找某一站k,使cost[i][k] + cost[k][j]最小
int temp = cost[i][k] + cost[k][j];
if (temp < cost[i][j]) {
cost[i][j] = temp;
}
}
}
}
}
int main() {
int n;//站点数
cin >> n;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
cin >> cost[i][j];
}
}
for (int i = 1; i < n; i++) {
cost[i][i] = 0;
}
findCheapest(cost, n);
cout << cost[1][n] << endl;
system("pause");
return 0;
}
总结
动态规划的一般思路
- 将原问题分解为子问题。子问题与原问题形式相同或类似,子问题求出就要保存解。
- 确定状态。列出状态转移方程。
- 确定初始状态和边界值。
适合用动规的问题
- 问题有最优解
- 子问题与原问题类似
参考资料
- 《计算机算法设计与分析》(第5版)王晓东编著
- 郑琪老师的PPT
https://blog.csdn.net/ailaojie/article/details/83014821
https://www.cnblogs.com/jacklovelol/p/6013111.html
组对编程小结
在组队上机的过程中,队友给了我很大的帮助,包括纠正我的状态转移方程、处理边界情况以及debug。总的来说,组对编程比单人更能发现自身的不足,提高编程A题的效率。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号