【斜优DP】bzoj4518-Sdoi2016征途

一、斜率优化DP与决策单调性

这里浅显（并且不严谨）地说明一下标题中的两个名词：

斜率优化DP：状态转移方程形如f[i]=min/max{f[k]+(x[i]-x[k])^y}的一类DP问题；

决策单调性：若对于状态i，有决策t<k，且k优于t，则对于任意状态v>i，存在决策k优于t。

对以上两条说明的不严谨与模糊之处，下文将结合题目给出（依旧不严谨且模糊的）一定程度上的解释。

二、题目

Description

Pine开始了从S地到T地的征途。

从S地到T地的路可以划分成n段，相邻两段路的分界点设有休息站。

Pine计划用m天到达T地。除第m天外，每一天晚上Pine都必须在休息站过夜。所以，一段路必须在同一天中走完。

Pine希望每一天走的路长度尽可能相近，所以他希望每一天走的路的长度的方差尽可能小。

帮助Pine求出最小方差是多少。

设方差是v，可以证明，v×m^2是一个整数。为了避免精度误差，输出结果时输出v×m^2。

Input

第一行两个数 n、m。

第二行 n 个数，表示 n 段路的长度

Output

 一个数，最小方差乘以 m^2 后的值

Sample Input

5 2
1 2 5 8 6

Sample Output

36

HINT

1≤n≤3000,保证从 S 到 T 的总路程不超过 30000

附上原题链接→_→Problem 4518. -- [Sdoi2016]征途

三、题目分析

为方便书写，作出如下约定：

a[i]：题目给出的第i段路程长；

sum[i]：路程长的前缀和；

x[i]：第i天走过的路程总和。

根据题意，每天走过的路程长度的方差表示为：

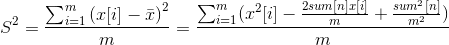
整理得：

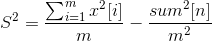
显然，由于上式中只有x[i]为变量，问题自然转化成了求∑x²[i]的最小值。

设计状态转移方程如下：

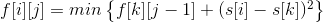
其中，f[i][j]表示前j天走过前i段路程，每天路程平方和的最小值。

观察到状态转移方程的形式基本符合斜率优化DP的形式，于是固定j，并：

令t<k：

当t优于k：

整理得：

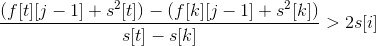
同理，当k优于t：

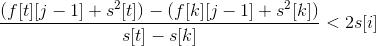
由于s[i]单调递增，故若在状态i下有k优于t，则对于任意v>i，存在k优于t。

这就意味着，如果我们在某个状态时发现决策k优于t，我们便再也不需要访问决策t了。这就利用决策单调性，达到了降低时间复杂度的效果。

此外，还可以发现，在某个状态下的有效决策形成了一个下凸壳。粗略证明如下：

设坐标系中存在点A、B、C，其横坐标单调递增，其对应决策简称为决策A、B、C

当B的纵坐标大于A、C的纵坐标（形成了一个上凸壳）：

1. 2s[i]<k_BC：决策A优于决策B，决策B优于决策C，故决策A最优；
2. k_BC<2s[i]<k_AB：决策A优于决策B，决策C优于决策B，故决策A或C最优；
3. 2s[i]>k_AB：决策B优于决策A，决策C优于决策B，故决策C最优。

以上，形成上凸壳时，决策B不可能成为最优决策，故删去点B，上凸壳性质被破坏；

同理，当B的纵坐标小于A、C的纵坐标（形成了一个下凸壳）：

1. 2s[i]<k_AB：决策A优于决策B，决策B优于决策C，故决策A最优；
2. k_AB<2s[i]<k_BC：决策B优于决策A，决策B优于决策C，故决策B最优；
3. 2s[i]>k_BC：决策B优于决策A，决策C优于决策B，故决策C最优。

故形成下凸壳时，所有决策均有可能成为最优决策。

这样，我们用一个双端队列就能维护可能成为最优决策的的决策，始终保证队首元素最优，队列满足下凸壳性质。

四、代码实现

其实f数组不需要开二维，因为我们每次只用到了f[i][j]和f[i][j-1]，所以可以再压去一维。但为方便理解，博主仍使用二维f数组。

#include<cstdio>
const int MAXN=3e3+10;
int n,m;
int s[MAXN];
int q[MAXN],l,r;
long long f[MAXN][MAXN];
double count_y(int k,int j){return f[k][j-1]+s[k]*s[k];}
double count(int t,int k,int j){return (count_y(t,j)-count_y(k,j))/(s[t]-s[k]);}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i)
    {
        int x;
        scanf("%d",&x);
        s[i]=s[i-1]+x;
    }
    for(int i=1;i<=n;++i)f[i][1]=s[i]*s[i];
    for(int j=2;j<=m;++j)
    {
        l=1,r=1;
        for(int i=1;i<=n;++i)
        {
            while(l<r&&count(q[l],q[l+1],j)<2*s[i])++l;
            int temp=q[l];
            f[i][j]=f[temp][j-1]+(s[i]-s[temp])*(s[i]-s[temp]);
            while(l<r&&count(q[r],i,j)<count(q[r-1],q[r],j))--r;
            q[++r]=i;
        }
    }
    printf("%lld\n",f[n][m]*m-(long long)s[n]*s[n]);
    return 0;
}

弱弱地说一句，本蒟蒻码字也不容易，转载请注明出处http://www.cnblogs.com/Maki-Nishikino/p/6523852.html