最大闭合子图

博客链接:传送门

最大权闭合子图

闭合图
首先，先了解什么是闭合图。闭合图一般指一个图中点的集合，从该集合中所有的点出发，能到达的点要求都必须在该点集中。也就是说，从该集合中出发，一定要回到该集合中，不能出到集合外。

最大权闭合子图，顾名思义，就是所有闭合子图中点权之和最大的那个，注意这里的权指的是点权，因为闭合图是对于点集而言的。

最大权闭合子图
了解完概念后，要知道如何求最大权闭合子图。大体的思路是借助最小割模型，让每一种闭合图通过变形后都能和一种割相对应，这样求最大权就是求最小割。

具体做法
构造一个新的流网络，建一个源点s和汇点t，从s向原图中所有点权为正数的点建一条容量为点权的边，从点权为负数的点向t建一条容量为点权绝对值的边，原图中各点建的边都建成容量为正无穷的边。然后求从s到t的最小割，再用所有点权为正的权值之和减去最小割，就是我们要求的最大权值和了。

证明
简单证明，如果不想看证明的可跳过。
如何从最大权闭合子图转化到最小割的呢？首先我们要知道简单割的定义，简单割指的是割集的所有边都是从s出发的边或终点是t的边。由此，我们知道在上述建图方式中的最小割一定是一个简单割，因为其图内部的边的流量是正无穷，所以最小割集一定不包含内部的边，是一个简单割。
然后我们需要证明闭合子图和简单割是一一对应的，从而我们求闭合子图的最值就是简单割的最小值，也就是建的新图的最小割。
我们假设一个闭合子图是v，流网络分成两个集合S和T，构成一个割集的情况。S包含的是v+s（闭合子图的点+源点）；T包含的是剩下的所有点（闭合子图外的点+汇点）。在这种情况下闭合子图v就和这个割[S，T]相对应，且这个割是个简单割：当前割的割集是S集合到T集合的所有边的集合，割集内一定不会出现原图内部的边，因为从S集合出发，若起点是s，则一定不包含原图内部的边，若起点是v，根据闭合子图的定义，回到的一定是v中的点，所以不包含到T集合中的点，因此该割一定是简单割。

这样我们就将闭合子图问题转化成了割的问题了，然后我们就要看看数量关系，找到最大权闭合子图和最小割间的数量表达式，就可以借助最小割模型计算最大权闭合子图了。
首先我们要找到最小割的计算表达式，下面是割集的所有情况：

我们将原图中的点分为两个集合，v1和v2，v1是闭合子图的点集，v2是原图中剩下的所有点，因此割的所有情况共有四种（S集合到T集合共四种情况），其中有两种情况不存在，第①种情况不存在是因为我们在建图时就不会建s到t的边，第②种情况不存在是根据闭合子图的定理，从v1出发的点一定会回到v1，不会到v2。这样割集就只剩两种情况s到v2和v1到t，根据见图方式可得：前者的容量和是v2中所有点权为正的和，后者容量和是v1中所有点权为负数的和的相反数，割集的容量之和就是v2中所有点权为正的和+v1中所有点权为负数的和的相反数。

然后我们再看我们要求的闭合子图权值之和的计算表达式：最大权值和就等于v1中所有的权值和，即v1中所有点权为正的和+v1中所有点权为负的和。

我们将上面求出来的两个表达式相加可得：割集容量之和+闭合子图权值之和=原图中所有点权为正数的点权之和（后面的相加后刚好抵消）。而等式的右边是个定值，我们为使闭合子图权值最大化，所以我们就要使得割集容量之和最小化，即求最小割的大小，再用所有点权为正的权值之和减去最小割，就是我们要求的最大权值了。
————————————————
版权声明：本文为CSDN博主「harry1213812138」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_45735851/article/details/113811882

例题:

P2762 太空飞行计划问题

题解:最大闭合子图+输出方案。

这题真的太费脑子了……一开始的想法太天真，就是先用源点连接仪器，然后仪器连实验，实验和实验自连，边权是实验的净收益，但是这样后来证明是不行的，因为题面的意思是多个实验可以共用一个仪器。所以说就算某个实验的收益为负数，但是它用到的仪器能为别的实验所用，那么就相当与你花了这个实验的赞助商给你的钱为别的实验买仪器。
实在想不出来，看题解。 应该的建图方法是源点连接实验，边权是实验经费，实验和仪器之间连inf，然后仪器和汇点之间连接，边权是买仪器的钱，这样跑出来的最大流用总经费减去就行了。
下面看图

 

 

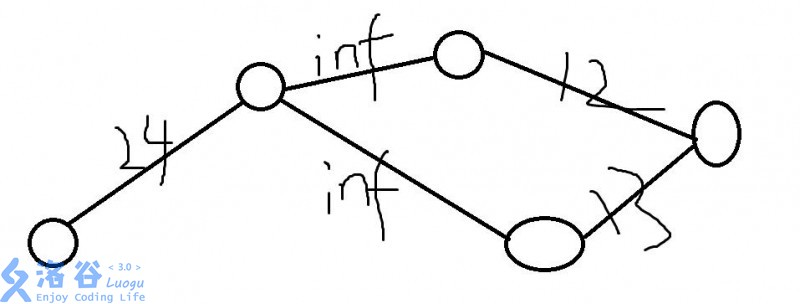
 这个图中就是一个明显的亏本实验，那么这么建图的话流到最后的就是24，赞助商给的经费，所以最后用总经费减去最大流的时候就直接减去这个经费，就相当于没选这个实验。

对于之前pass掉我程序的那个想法，用这种建图也可以实现。

 

 

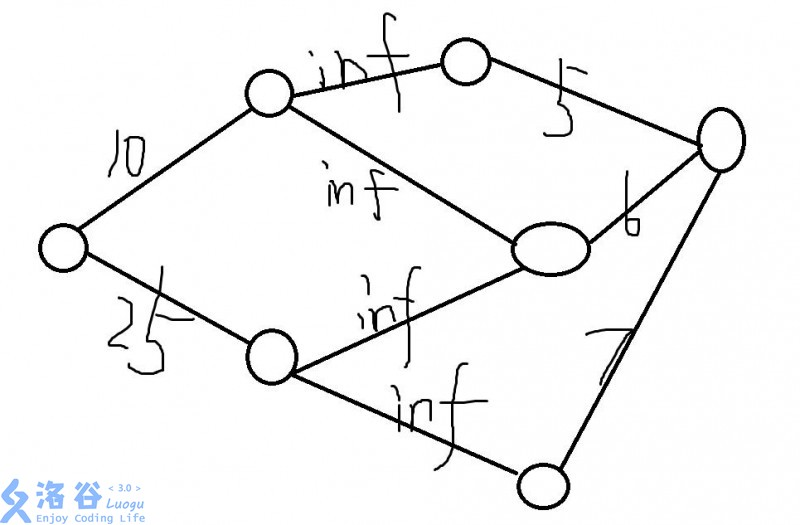
 正确性显然。
这个题最难的一点就在于如何输出方案。介入本人太蒟蒻，只能看题解。题解提供的方案是最后一遍增广的分层图中有层数的，也就是遍历到的点是选过的。这个大概的解释方法就是整张图看做最小割之后分成了两个集合，一个包括源点，一个包括汇点。
为什么要看做最小割呢？之前我们说过，如果某个实验的收益为负数，但是它用到的仪器能为别的实验所用，那么就相当与你花了这个实验的赞助商给你的钱为别的实验买仪器，具象化在这个图上，就是仪器那个点给这个实验一个流，把这个实验流出去的抵消掉了。当然，也会存在那种无论怎么买仪器都不划算的实验，这样的实验有一个特点，因为它不能供给仪器的需求，所以源点到它的残流一定是0，就是说不管是正向边还是反向边都是0，同样的那些可以供给的，源点到它的残留一定大于0，也就是正向边或者反向边大于0，说明做这个实验能赚钱。
那么，因为这种必须要删掉的实验，它的经费最终肯定要从总经费里面减掉，我们就不算它，而剩下的那些实验，它们所需要的仪器一起流到汇点，就是最大流。所以说，最小割也是割掉这些仪器与汇点之间的边。
由此我们可以证出，在最小割中，与源点同一集合的实验和仪器，必选。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define rint register int
#define inv inline void
#define inb inline bool
#define ini inline int
#define big 1e9
using namespace std;
int n,m,all,cnt,head[10001],cur[10001],dis[10001],ans,tot,s=0,t=151;
bool flag;
struct node
{
    int from,to,dis,num,next;
}ljb[10001];
ini read()
{
    char c;int r=0;
    while (c<'0' || c>'9') c=getchar();
    while (c>='0' && c<='9')
    {
        r=r*10+c-'0';
        c=getchar();
    }
    if (c=='\r') flag=1;
    return r;
}
inv add(int x,int y,int z)
{
    ljb[++cnt].from=x;
    ljb[cnt].to=y;
    ljb[cnt].dis=z;
    ljb[cnt].num=cnt;
    ljb[cnt].next=head[x];
    head[x]=cnt;
}
queue<int> q;
inb bfs()
{
    q.push(s);
    memset(dis,128,sizeof(dis));
    dis[s]=0;
    while(!q.empty())
    {
        int x=q.front();
        q.pop();
        for (rint i=head[x];i!=-1;i=ljb[i].next)
        {
            int y=ljb[i].to;
            if (dis[y]<0 && ljb[i].dis>0)
            {
                dis[y]=dis[x]+1;
                q.push(y);
            }
        }
    }
    if (dis[t]>0) return 1;
    return 0;
}
ini dfs(int x,int low)
{
    if (x==t) return low;
    for (rint& i=cur[x];i!=-1;i=ljb[i].next)
    {
        int y=ljb[i].to;
        if (dis[y]==dis[x]+1 && ljb[i].dis>0)
        {
            int flow=dfs(y,min(low,ljb[i].dis));
            if (flow)
            {
                ljb[i].dis-=flow;
                ljb[ljb[i].num^1].dis+=flow;
                return flow;
            }
        }
    } 
    return 0;
} 
int main()
{
    m=read();n=read();
    for (rint i=s;i<=t;i++) head[i]=-1;cnt=-1;
    for (rint i=1;i<=m;i++)
    {
        int x;x=read();all+=x;
        add(s,i,x);add(i,s,0);
        flag=0;
        while (!flag)
        {
            x=read();
            add(i,x+50,big);
            add(x+50,i,0);
        }
    }
    for (rint i=1;i<=n;i++)
    {
        int x;x=read();
        add(i+50,t,x);
        add(t,i+50,0);
    }
    while (bfs())
    {
        for (rint i=s;i<=t;i++) cur[i]=head[i];
        do
        {
            tot=dfs(s,big);
            ans+=tot;
        }
        while (tot);
    }
    for (rint i=1;i<=m;i++) if (dis[i]>0) cout<<i<<" ";
    printf("\n");
    for (rint i=1;i<=n;i++) if (dis[i+50]>0) cout<<i<<" ";
    printf("\n");
    printf("%d",all-ans);
 }