hdu4421Bit Magic(2-SAT)

题目描述:

Yesterday, my teacher taught me about bit operators: and (&), or (|), xor (^). I generated a number table a[N], and wrote a program to calculate the matrix table b[N][N] using three kinds of bit operator. I thought my achievement would get teacher's attention.
The key function is the code showed below.

 

 

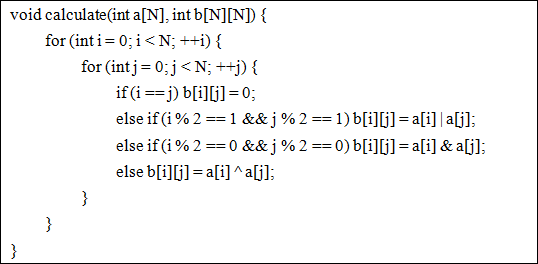
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?

题目大意:就上面这个图。

思路:对每一位根据上面的三种运算,进行2-SAT建图,如果某一个数的某一位的0,1同时出现在一个SCC里,则能不满足。

我真的要死了,调了两个多小时了,感觉好坑啊,最开始的代码和题解差别还蛮大的,我真搞不动了,到后面和题解一模一样

都A不了,但题解就是对的,有种被生活磨平了棱角,还被生活暴打的感觉,写题解都有气无力了,虽然没A，还是总结一下吧

如果是只能选择特定点情况,比如这题假如 b[i][j]=1101,第二种或操作,如果a[i]的第三位和a[j]的第三位都只能取0,这种关系能形成

什么矛盾关系呢,答案是如果a[i]的第三位取1的话就与a[i]的第三位取0连边,这样a[i]第三位的1所在的SCC就会包含与之相反的0,

这样就不满足题设条件了,就是代码注释哪里,好,口胡结束,真顶不住了,洗澡去了,明天好好休息一天

博客链接:https://blog.csdn.net/u013761036/article/details/32715111

题解代码:

#include<stdio.h>
#include<string.h>
#include<stack>

#define N_node 1000 + 50
#define N_edge 1000000 + 100

using namespace std;

typedef struct
{
        int to ,next;
}STAR;

STAR E[N_edge];
int list[N_node] ,tot;
int DFN[N_node] ,LOW[N_node];
int Belong[N_node];
int Index ,num ,okk;
int instack[N_node];
int B[550][550];
stack<int>st; 

void add(int a ,int b)
{
   E[++tot].to = b;
   E[tot].next = list[a];
   list[a] = tot;
}

int minn(int x ,int y)
{
   return x < y ? x : y;
}

void Tarjan(int s)
{
   DFN[s] = LOW[s] =  Index ++;
   st.push(s);
   instack[s] = 1;
   for(int k = list[s] ;k ;k = E[k].next)
   {
      int to = E[k].to;
      if(!DFN[to])
      {
         Tarjan(to);
         LOW[s] = minn(LOW[to] ,LOW[s]);
      }
      else if(instack[to])
      {
         LOW[s] = minn(DFN[to] ,LOW[s]);    
      }
   }
   if(LOW[s] == DFN[s])
   {
      num ++; 
      while(1)
      {
         int v = st.top();
         Belong[v] = num;
         st.pop();
         instack[v] = 0;
         if(v == s) break;
      }
   }
}

bool ok(int n)
{
    memset(instack ,0 ,sizeof(instack));
    memset(DFN ,0 ,sizeof(DFN));
    memset(LOW ,0 ,sizeof(LOW));
    while(!st.empty()) st.pop();
    Index = 1 ,num = 0;
    for(int i = 0 ;i < n * 2 ;i ++)
   {
    if(DFN[i]) continue;
    Tarjan(i);
   }
   for(int i = 0 ;i < n * 2 ;i += 2)
   if(Belong[i] == Belong[i^1]) return 0;
   return 1;
}
                    
                    
bool solve(int n )
{
    for(int i = 0 ;i < n ;i ++)
    if(B[i][i]) return 0;
    __int64 Key = 1;
    for(int ii = 1 ;ii <= 32 ;ii ++ ,Key *= 2)
    {
       memset(list ,0 ,sizeof(list));
       tot = 1;
       for(int i = 0 ;i < n ;i ++)
       for(int j = 0 ;j < n ;j ++)
       {
          if(i == j) continue;
          int now = B[i][j] & Key;
          if(i % 2 && j % 2)
          {
            if(!now)
            add(i * 2 ,i * 2 + 1) ,add(j * 2 ,j * 2 + 1);//就是这里的矛盾关系
            else add(i * 2 + 1 ,j * 2) ,add(j * 2 + 1 ,i * 2);
          }
          else if(i % 2 == 0 && j % 2 == 0)
          {
              if(!now) 
              add(j * 2 ,i * 2 + 1) ,add(i * 2 ,j * 2 + 1);//还有这里
              else add(i * 2 + 1 ,i * 2) ,add(j * 2 + 1 ,j * 2);
          }
          else
          {
              if(!now)
              add(i * 2 ,j * 2) ,add(i * 2 + 1 ,j * 2 + 1),
              add(j * 2 ,i * 2) ,add(j * 2 + 1 ,i * 2 + 1);
              else
              add(i * 2 ,j * 2 + 1) ,add(j * 2 ,i * 2 + 1),
              add(i * 2 + 1 ,j * 2) ,add(j * 2 + 1 ,i * 2);
          }
       }
       if(!ok(n)) return 0;
    }
    return 1;
} 

int main ()
{
    int n ,i ,j;
    while(~scanf("%d" ,&n))
    {
       for(i = 0 ;i < n ;i ++)
       for(j = 0 ;j < n ;j ++)
       scanf("%d" ,&B[i][j]);
       solve(n) ? puts("YES") : puts("NO");
    }
    return 0;
}           
     

我最初的代码:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 300000;
struct edge {
    int f, t, nxt;
}e[maxn];
int hd[maxn], tot;
void add(int f, int t) {
    e[++tot] = { f,t,hd[f] };
    hd[f] = tot;
}
int n, m;
int low[maxn], dfn[maxn], cnt;
int stk[maxn], sk, instk[maxn], col[maxn], colnum;
bool f;
void init() {
    memset(dfn, 0, sizeof(dfn));
    memset(col, 0, sizeof(col));
    memset(hd, 0, sizeof(hd));
    sk = tot = colnum = cnt = 0;
}
void dfs(int u) {//缩点模板
    low[u] = dfn[u] = ++cnt;
    stk[++sk] = u; instk[u] = 1;
    for (int i = hd[u]; i; i = e[i].nxt) {
        int v = e[i].t;
        if (!dfn[v]) {
            dfs(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instk[v]) {
            low[u] = min(low[u], dfn[v]);
        }
    }
    if (low[u] == dfn[u]) {
        colnum++;
        while (1) {
            int v = stk[sk--];
            instk[v] = 0;
            if (col[v ^ 1] == colnum) {
                f = 0; 
            }
            col[v] = colnum;
            if (v == u)break;
        }
    }
}
int main() {
    //freopen("test.txt", "r", stdin);
    while (~scanf("%d", &n)) {
        init();
        f = 1;
       //把所有位直接建到一个图里面,然而不得行。
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                int b; scanf("%d", &b);
                if (i == j) { if(b)f = 0; continue;}
                else if (i % 2 == 1 && j % 2 == 1) {
                    for (int k = 0; k < 32; k++) {
                        int l = (i * 32 + k) * 2, r = (j * 32 + k) * 2;
                        if (b & (1 << k)) {
                            //(l,r)矛盾
                            add(l, r ^ 1);
                            add(r, l ^ 1);
                        }
                        else {
                            add(l^1, l);
                            add(r^1, r);
                        }
                    }
                }
                else if (i % 2 == 0 && j % 2 == 0) {
                    for (int k = 0; k < 32; k++) {
                        int l = (i * 32 + k) * 2, r = (j * 32 + k) * 2;
                        if (b & (1 << k)) {
                            add(l, l ^ 1);
                            add(r, r ^ 1);
                        }
                        else {
                            //(l^1,r^1)矛盾
                            add(l ^ 1, r);
                            add(r ^ 1, l);
                        }
                    }
                }
                else {
                    for (int k = 0; k < 32; k++) {
                        int l = (i * 32 + k) * 2, r = (j * 32 + k) * 2;
                        if (b & (1 << k)) {
                            //(l,r)矛盾
                            add(l, r ^ 1);
                            add(r ^ 1, l);
                            //(l^1,r^1)矛盾
                            add(l ^ 1, r);
                            add(r, l ^ 1);
                        }
                        else {
                            //(l,r^1)矛盾
                            add(l, r);
                            add(r, l);
                            add(r ^ 1, l ^ 1);
                            add(l ^ 1, r ^ 1);
                        }
                    }
                }
            }
        }
        for (int i = 0; i < 32 * 2 * n&&f; i++) {
            if (!dfn[i]) {
                dfs(i);
            }
        }
        if (f) {
            printf("YES\n");
        }
        else {
            printf("NO\n");
        }
    }
    return 0;
}