hdu1667(IDA*)

题目描述:

The Rotation Game

Problem Description

The rotation game uses a # shaped board, which can hold 24 pieces of square blocks (see Fig.1). The blocks are marked with symbols 1, 2 and 3, with exactly 8 pieces of each kind.

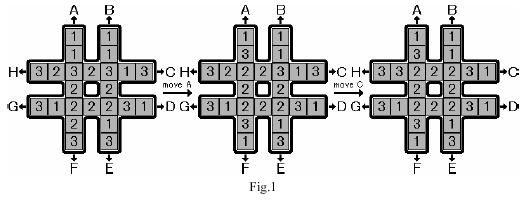
Initially, the blocks are placed on the board randomly. Your task is to move the blocks so that the eight blocks placed in the center square have the same symbol marked. There is only one type of valid move, which is to rotate one of the four lines, each consisting of seven blocks. That is, six blocks in the line are moved towards the head by one block and the head block is moved to the end of the line. The eight possible moves are marked with capital letters A to H. Figure 1 illustrates two consecutive moves, move A and move C from some initial configuration.

 

思路:嗯,深度无限深,广度也很广,迭代加深应该比较好想到(我口胡的),但是这题是真的快乐,好多麻烦的地方,

有八种移动的方式,每种方式要移动7个方块,所以要开一个二维数组记录,还必须手打,而且这题回溯可以不用

记录之前的状态,因为每种移动方式和另一种移动方式是相反的,所以我们只需要记录每一种移动方式相对应

的移动方式,然后回溯调用,反向移动即可,而且你不这样做也会爆栈的^_^,中心地八个点地坐标也需要用一个数组

标记起来,用来判断是否已经满足,然后就是总体设计了

迭代加深,每次只移动depth深度,不停地加深depth,知道求出解,A*剪枝，就是你中心的可能最少移动次数=(8-任意数字在中心位置的最大出现次数)

如果大于depth,说明这样走下去也不肯能有解,不得行,所以剪掉,还是看代码吧,学长给我调了半天hh

AC代码:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 100;
const int inf = 0x3f3f3f3f;
int center[8] = { 6,7,8,11,12,15,16,17 };
int reveropt[8] = { 5,4,7,6,1,0,3,2 };
int change[8][7] = {
    {0,2,6,11,15,20,22},
    {1,3,8,12,17,21,23},
    {10,9,8,7,6,5,4},
    {19,18,17,16,15,14,13},
    {23,21,17,12,8,3,1},
    {22,20,15,11,6,2,0},
    {13,14,15,16,17,18,19},
    {4,5,6,7,8,9,10}
};
int tmp[24];
int cnt[5];
int get() {//找出8-出现次数最多的数的出现次数,即至少需要移动的次数
    int maxcnt = 0;
    memset(cnt, 0, sizeof(cnt));
    for (int i = 0; i < 8; i++) {
        cnt[tmp[center[i]]]++;
        maxcnt = max(maxcnt, cnt[tmp[center[i]]]);
    }
    return 8 - maxcnt;
}
void option(int opt) {//移动
    int t = tmp[change[opt][0]];
    for (int j = 0; j < 6; j++) {
        tmp[change[opt][j]] = tmp[change[opt][j + 1]];
    }
    tmp[change[opt][6]] = t;
}
string res;
int depth;
bool dfs(int step, int lastopt) {
    int last = get();
    if (step + last >= depth) return false;//已经移动+至少需要移动>预设深度
    if (!last) {//中心点全都相同了
        printf("%s\n", res.c_str());
        printf("%d\n", tmp[center[0]]);
        return true;
    }
    for (int i = 0; i < 8; i++) {
        if (lastopt != -1 && i == reveropt[lastopt])continue;//如果与上次操作刚好相反的就不要
        res.push_back('A' + i);
        option(i);//移动
        if (dfs(step + 1, i))return true;
        option(reveropt[i]);//回溯
        res.pop_back();
    }
    return false;
}
int main() {
    //freopen("test.txt", "r", stdin);
    while (~scanf("%d", &tmp[0])) {
        if (tmp[0] == 0)break;
        for (int i = 1; i < 24; i++) {
            scanf("%d", &tmp[i]);
        }
        res.clear();
        if (!get()) {
            printf("No moves needed\n%d\n",tmp[center[0]]); continue;
        }
        depth = 1;
        while (1) {
            if (dfs(0, -1))break;
            depth++;
        }
    }
    return 0;
}