勤奋的杨老师（二）(最大流)

题目描述:

链接：https://ac.nowcoder.com/acm/problem/15828
来源：牛客网

众所周知，杨老师是一位十分勤奋的老师，他非常的热爱学习。

勤奋的他为自己罗列了一个学习清单，共有n个知识点，他可以有选择的进行学习。

每个知识点都会对应0个或1个或多个先修知识点（只有学会了先修知识点才能学习该知识点），同时每个知识点都有一个智慧值和一个智力消耗值。

杨老师希望在进行过激烈的学习之后，他的收获可以·量化为所有学过的题的智慧值的和与智力消耗值的和的差值。请问，这个值最大是多少？

输入描述:

第一行：一个整数n（n<=500）接下来n行，每行两个整数，代表第i个知识点的智慧值和智力消耗值接下来若干行，每行2个整数u, v，代表u是v的先修知识点。

输出描述:

一行，表示杨老师的收获的最大值
思路:看的题解,这道题一眼看过去都感觉要用树形dp了,但是这里面的图有闭合,不能用,
而最大流却能解决这种问题,设cnt为所有直接选取为赚的节点的和,v为该点获取智慧值-消耗智慧值,如果为负,则源点与其连边,流量为-v
如果为正,则该点与汇点连边,流量为v,如果a是b的前置点,这a与b连边,流量为inf,然后跑一遍最大流,
得到的就是所有直接选取为负的节点,它对以它为前驱(直接或者间接)的其余直接选取为正的点的影响,然后用tot减去该影响,就是能获取的
最大价值.
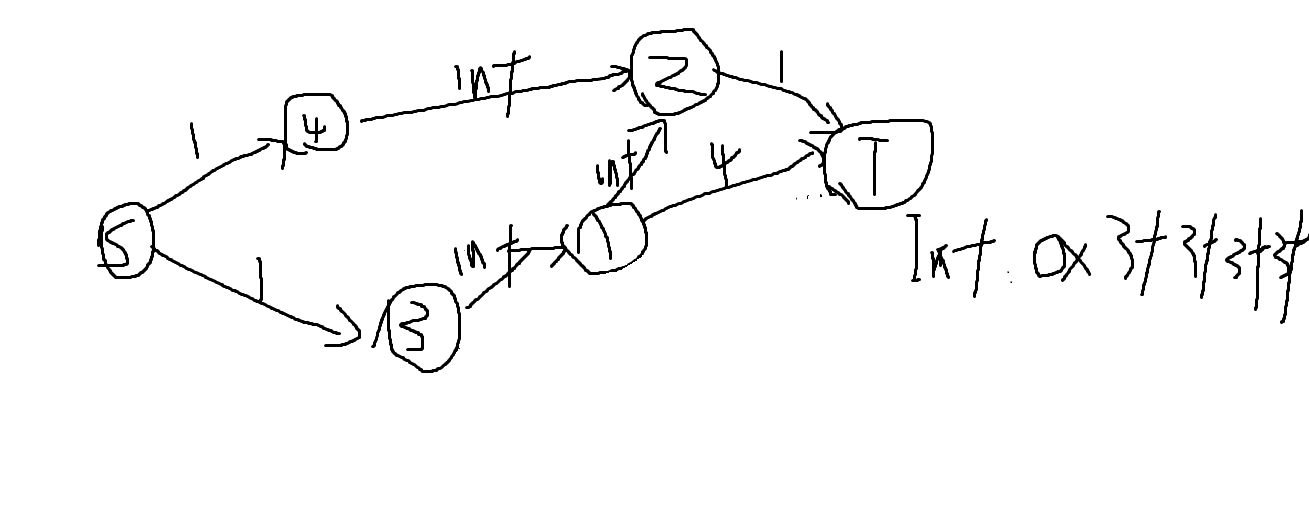
下面是以样例为例子花的图：

如图跑最大流得到的就是3,4号点对后面1,2号点的取值的影响,减去这部分影响,就是最大价值
AC代码:

#include<bits/stdc++.h>
using namespace std;
const int maxn = 505;
const int maxm = 60005;
const int inf = 0x3f3f3f3f;//之前搞成1e15,有精度损失..
double esp = 1e-6;
struct edge {
    int t, nxt;
    int w;
}e[maxm];
int hd[maxn], tot = 1;
void add(int f, int t, int w) {
    e[++tot] = {t,hd[f],w};
    hd[f] = tot;
    e[++tot] = {f,hd[t],0};
    hd[t] = tot;
}
int n, s, t;
int cur[maxn], dep[maxn];
bool bfs() {
    memset(dep, 0, sizeof(dep));
    dep[s] = 1;
    queue<int>q;
    q.push(s);
    cur[s] = hd[s];
    while (!q.empty()) {
        int u = q.front(); q.pop();
        for (int i = hd[u]; i; i = e[i].nxt) {
            int v = e[i].t, w = e[i].w;
            if (w > 0 && !dep[v]) {
                dep[v] = dep[u] + 1;
                cur[v] = hd[v];
                if (v == t)return true;
                q.push(v);
            }
        }
    }
    return false;
}
int dfs(int u, int flow) {
    if (u == t)return flow;
    int rest = flow;
    for (int i = cur[u]; i; i = e[i].nxt) {
        int v = e[i].t, w = e[i].w;
        if (dep[v] == dep[u] + 1 && w > 0) {
            int tmp = dfs(v, min(rest, w));
            if (!tmp)dep[v] = 0;
            rest -= tmp;
            e[i].w -= tmp;
            e[i ^ 1].w += tmp;
            if (!rest)break;
        }
    }
    return flow - rest;
}
int dinic() {
    int ans = 0;
    while (bfs()) {
        ans += dfs(s, inf);
    }
    return ans;
}
int main() {
    //freopen("test.txt", "r", stdin);
    scanf("%d", &n);
    s = n+1, t = n + 2;
    int a, b,cnt=0;
    for (int i = 1; i <= n; i++) {
        scanf("%d%d", &a, &b);
        int v = a - b;
        if (v > 0) {//如果大于零直接与汇点相连
            cnt += v; add(i, t, v);
        }
        else {//小于零,则与源点相连
            add(s, i, -v);
        }
    }
    int u, v;
    while (~scanf("%d%d", &u, &v)) {
        add(u, v,inf);
    }
    cout <<cnt- dinic() << endl;//减去所有负起点能够流出的最大流
    return 0;
}