hdu1540(线段树维护连续子区间)

hdu1540

意思是让我们维护一段连续序列,可能从某个点断开,查询某个连续序列的长度

我们只需要维护某段小区间的连续前缀个数以及连续后缀个数,在查询的时候就能很好的将两个区间合并到一起

以及一个siz记录大小,flg判断是否能往上继续增长

查询的时候要用两个flg标记该合并的时候是否可取

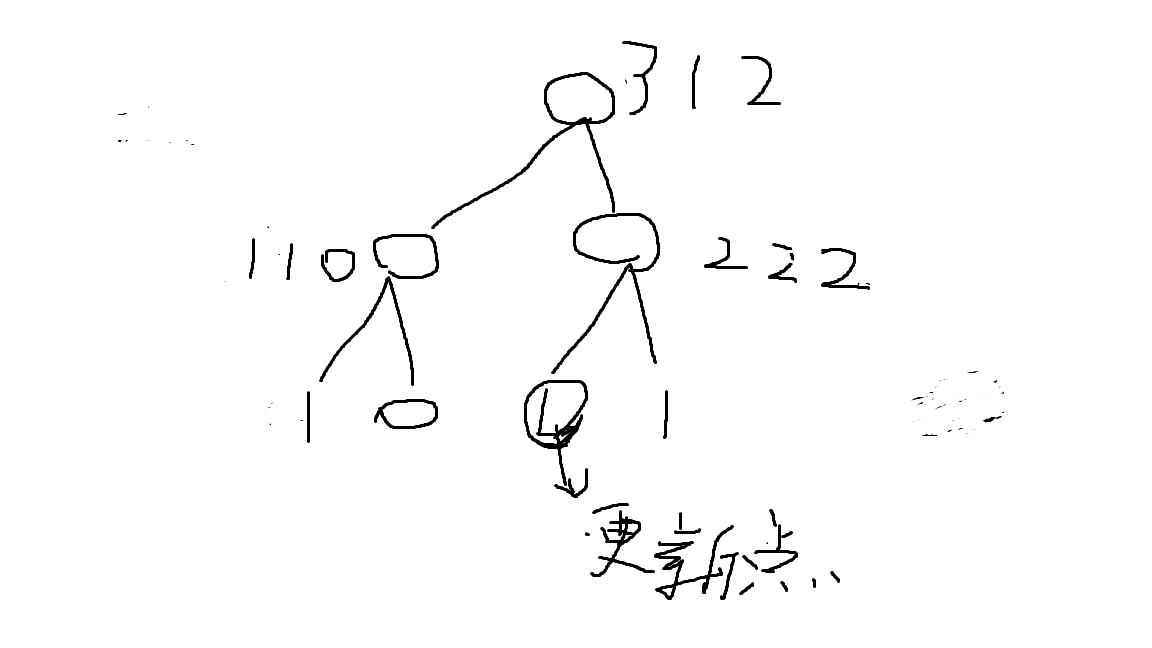
第一个数是siz,第二个数是前缀数,第三个数是后缀数,然后每次有点更新都在push_up里面更新这些数即可

具体怎么更新和查询的可以看代码和注释,手写太费劲了

还有我要吐槽一下hdu的那个题目,都不说测试用例很多个,我连续被坑了两次。。。

代码:

#include<iostream>
#include<string>
#include<stack>
#include<queue>
#include<string.h>
#include<map>
#include<set>
#include<vector>
#include<iomanip>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn = 5e4 + 1;
inline int read()
{
    int f = 1, num = 0;
    char ch = getchar();
    while (0 == isdigit(ch)) { if (ch == '-')f = -1; ch = getchar(); }
    while (0 != isdigit(ch)) num = (num << 1) + (num << 3) + ch - '0', ch = getchar();
    return num * f;
}
#define ls(x) x<<1
#define rs(x) x<<1|1
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
int ll[maxn << 2], rr[maxn << 2], siz[maxn << 2];//ll前缀连续个数,rr后缀连续个数,siz总个数
void push_up(int rt) {
    if (siz[ls(rt)] == ll[ls(rt)]) {
        //如果左区间的前缀数是等于他本身的大小的,说明完全是满的,所以合并后区间的前缀是左区间的连续前缀(大小)加上右区间的连续前缀
        ll[rt] = ll[ls(rt)] + ll[rs(rt)];
    }
    else {//如果不是,说明左区间有断开的点,所以合并后的区间的前缀就是左区间的前缀咯
        ll[rt] = ll[ls(rt)];
    }
    //后缀同理
    if (siz[rs(rt)] == rr[rs(rt)]) {
        rr[rt] = rr[rs(rt)] + rr[ls(rt)];
    }
    else {
        rr[rt] = rr[rs(rt)];
    }
}
//有了push_up其余操作就比较简单了
inline void build(int rt, int l, int r) {
    siz[rt] = ll[rt] = rr[rt] = (r - l + 1);//siz只需要初始化一次即可,最开始都是村庄完好的,所以都取最大
    if (l == r) {
        return;
    }
    int mid = (l + r) >> 1;
    build(lson);
    build(rson);
}
void update(int rt, int l, int r, int pos, int f) {//f为1代表该点恢复,为0代表该点断开
    if (l == r) {
        if (f) {
            ll[rt] = rr[rt] = 1;
        }
        else {
            ll[rt] = rr[rt] = 0;
        }
        return;
    }
    int mid = (l + r) >> 1;
    if (pos <= mid) {
        update(lson, pos, f);
    }
    else {
        update(rson, pos, f);
    }
    push_up(rt);
}
int qurry(int rt, int l, int r, int pos, bool& flg1, bool& flg2) {
    //flg1(查询节点是当前在当前区间的前缀中的)表示左边还要扩散,flg2表示右边还要扩散
    if (l == r) {
        if (ll[rt] == 0) {//如果都不存在就返回0
            flg1 = flg2 = 0; return 0;
        }
        else {
            flg1 = flg2 = 1;//存在就从下向上一步步查询
            return 1;
        }
    }
    int mid = (l + r) >> 1;
    int res;
    if (pos <= mid) {
        res = qurry(lson, pos, flg1, flg2);
        if (flg2) {
//从左区间查询后如果还需要像右区间扩散就+上右区间的前缀,如果右区间还是满的
//,就可能还要往右扩散,不然的话就标记flg2=0,不再向右扩散
            res += ll[rs(rt)];
            if (ll[rs(rt)] != siz[rs(rt)]) {
                flg2 = 0;
            }
        }
    }
    else {
        res = qurry(rson, pos, flg1, flg2);
        if (flg1) {//与上同理
            res += rr[ls(rt)];
            if (rr[ls(rt)] != siz[ls(rt)]) {
                flg1 = 0;
            }
        }
    }
    return res;
}
int n, m;
vector<int>D;
int main() {
    //freopen("test.txt", "r", stdin);
    while (~scanf("%d%d", &n, &m)) {//hdu都不带提醒人的,我还想半天
        build(1, 1, n);
        D.clear();
        for (int i = 1; i <= m; i++) {
            char c; int x;
            cin >> c;
            if (c == 'D') {
                x = read();
                update(1, 1, n, x, 0);
                D.push_back(x);
            }
            else if (c == 'Q') {
                x = read();
                bool flg1 = 0, flg2 = 0;//初始化无所谓,反正是从地下往上面推
                printf("%d\n", qurry(1, 1, n, x, flg1, flg2));
            }
            else {
                x = D.back(); D.pop_back();
                update(1, 1, n, x, 1);
            }
        }
    }
    return 0;
}