Beyond Independent Relevance: Methods and Evaluation Metrics for Subtopic Retrieval

目录

• 概
• 符号说明
• S-recall and S-precision

Zhai C., Cohen W. W. and Lafferty J. Beyond independent relevance: methods and evaluation metrics for subtopic retrieval. In International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR), 2003.

概

本文讨论如何评估 diversity (虽然后面也介绍了如何平衡相关性和多样性).

符号说明

• \(\mathcal{I}\), items;
• \(\mathcal{C}\), 类别.

S-recall and S-precision

• 假设给定了一个 rank list \(R = [i_1, i_2, \cdots, i_K]\), 然后每个 item \(i\) 所对应的类别为:

  \[c(i) \subset \mathcal{C}. \]

  则概 rank list 的 diversity 可以通过如下 S-recall 指标进行评估:

  \[\text{S-Recall@K} := \frac{|\bigcup_{k=1}^K c(i_k)|}{|\mathcal{C}|}. \]

• 但是如果我们细想会发现, \(\text{S-Recall}@K\) 的值本身可能并不能够很好反映出多样性的差异. 把比如:

  1. \(c(i) = \{a_i\}, i=1,2,\cdots, K\), 且 \(a_i \not= a_j, i \not= j\);
  2. \(c(i) = \{a_i\} \cup O\), 其中 \(O \subset \{a_1, a_2, \ldots, a_K\}\).

• 显然, 在Top-\(K\) 的情况下, 二者的 \(\text{S-Recall@K}\) 是一致的, 但是可能第二种情况会更加好一点, 因为后者在 \(< K\) 的情形下始终有更优的 \(\text{S-Recall}\). 当然, 这个例子其实有一点点的不合理, 因为这似乎意味着, 为了追求多样性, 我们应该去追寻那些'多类'的 items, 这其实和我们想要的多样性是有出入的.

• 一个更易比较的指标是:

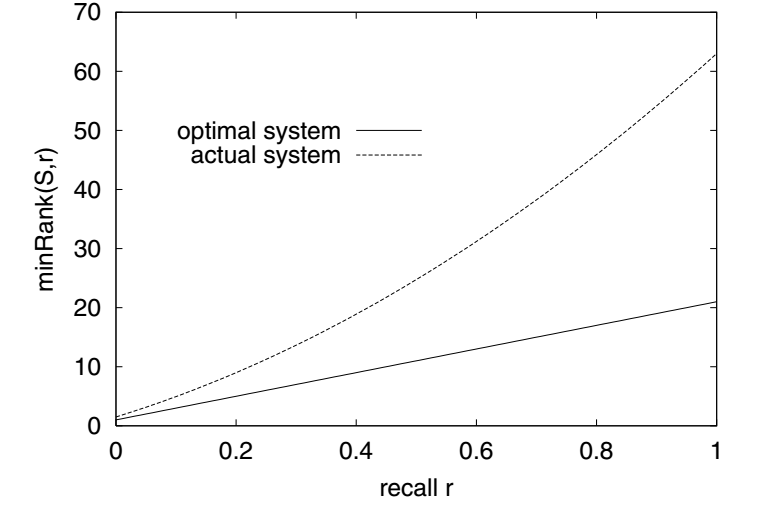
  \[\text{S-Precision@r} := \frac{\text{minRank}(R_{opt}, r)}{\text{minRank}(R, r)}, \]

  其中 \(R, R_{opt}\) 分别表示当前的推荐列表, 以及根据 \(\text{S-Recall}\) 得到的最优的推荐列表. \(0 \le r \le 1\) 是一个 recall level, \(\text{minRank}(R, r)\) 是使得最小的 rank \(K\) 使得整体的 \(\text{S-Recall}@K\) 能够达到 level \(r\). 下图给出了一个实际的比较: