Handing Incomplete Heterogeneous Data using VAEs
概
这篇文章利用VAE处理缺失数据, 以往的对缺失数据的处理往往是不区分连续离散, 数字符号的, 感觉这里利用分布的处理方式非常精彩.
主要内容
ELBO
首先, 既然是利用VAE, 那么就需要推导出相应的ELBO来.
文章首先假设数据\(x\)和隐变量之间关系满足:
\[p(x_n, z_n) = p(z_n) \prod_d p(x_{nd}|z_n),
\]
即\(x_n\)的各分量关于\(z_n\)的条件独立的.
进一步引入观测数据\(x^o\)和\(x^m\), 即
\[x^o_{nd} =
\left \{
\begin{array}{ll}
x_{nd}, & d \in \mathcal{O}_n \\
0, & d \in \mathcal{M}_n
\end{array}
\right ., \\
x^{m}_n = x_n - x_{n}^o.
\]
其中\(\mathcal{O}, \mathcal{M}\) 分别是观测的元素和缺失的元素位置, 且彼此是互斥的.
那么
\[p(x_n|z_n) = \prod_{d \in \mathcal{O}_n} p(x_{nd}|z_n) \prod_{d \in \mathcal{M}_n} p(x_{nd}|z_n).
\]
\[q(z_n, x_n^m|x_n^o) = q(z_n|x_n^o) \prod_{d \in \mathcal{M}_n} p(x_{nd}|z_n).
\]
则通过极大似然即可推出ELBO:
\[\begin{array}{ll}
\log p(X^o)
&= \sum_{n} \mathbb{E}_{q(z_n|x_n^o)} \log \frac{p(x_n^o, z_n)}{q(z_n|x_n^o)} \frac{q(z_n|x_n^o)}{p(z_n|x^o_n)} \\
&\ge \sum_n \mathbb{E}_{q(z_n|x_n^o)} \log p(x_n^o|z_n)
- \sum_n \mathrm{KL}(q(z_n|x_n^o)\| p(z_n)).
\end{array}
\]
其中\(p(x_n^o|z_n)=\prod_{d \in \mathcal{O}_n} p(x_{nd}|z_n)\).
网络结构
从上面的假设就可以看出, 整体的VAE的结构是这样的:
- 观测数据\(x^o\)经过encoder得到\(\mu_q(x^o), \Sigma_q(x^o)\), 并从高斯分布中采样得到\(z\).
- 隐变量\(z\)经过独立的网络\(h_1, \cdots, h_d\)得到预测的数据\(\gamma_1, \gamma_2, \cdots, \gamma_d\), 这些用于构建各自的分布\(p(x_d|\gamma_d)\), 这个分布是数据的类型而不同.
不同的数据
这对不同的数据类型, 可以假设不同的分布\(p(x_d|\gamma_d)\), 这我认为是非常有趣的一个点.
- 如果\(x_d\)是实值变量, 则可以假设其为高斯分布:
\[p(x_d|\gamma_d) = \mathcal{N} (x_d|\mu_d(z), \sigma_d^2(z)).
\]
- 如果\(x_d \in \mathbb{R}^+\), 则
\[\log p(x_d|\gamma_d) = \mathcal{N} (x_d|\mu_d(z), \sigma_d^2(z)), x_d \ge 0.
\]
- \(x_d \in \{0, 1, 2, \cdots \}\), 则假设poisson分布:
\[p(x_d|\gamma_d) = \mathrm{Poiss}(x_d|\lambda(z))
= \frac{\lambda_d(z)^{x_d} \exp (-\lambda_d(z_n))}{x_d!}.
\]
- 类别数据, \(\gamma_d \in \{h_{d0}(z), \cdots, h_{d(R-1)}(z)\}\)此时为logits, 最后的概率分布
\[p(x_d = r|\gamma_d) = \frac{\exp (-h_{dr}(z))}{\sum_r \exp (-h_{dr}(z))}
\]
- Ordinal data
\[p(x_d = r | \gamma_d) = p(x_d \le r|\gamma_d)-p(x_d \le r-1|\gamma_d),
\]
其中
\[p(x_d \le r|\gamma_d) = \frac{1}{1 + \exp (-(\theta_r(z)- h_d(z)))}.
\]
HI-VAE
上述的假设有些过于强了, 为此, 作者做出了一些调整.
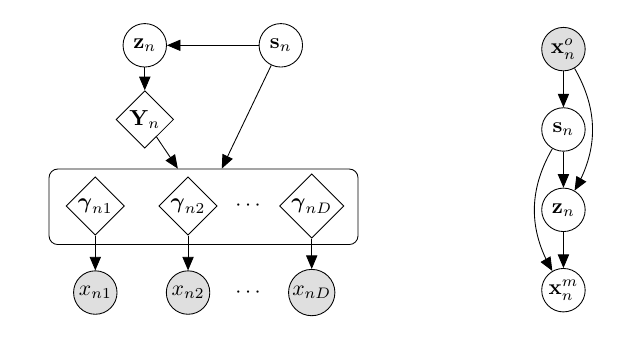
- 假设一个了一个混合的高斯先验: \(p(z|s_n)\);
- 隐变量需要先经过一个共同的变化得到\(Y_n\)再和\(s_n\)一起经过独立的网络得到\(\gamma_1, \gamma_2, \cdots, \gamma_d\).
个人感觉第二点的设计还是不错的.
