Recovering Low-Rank Matrices From Few Coefficients In Any Basis

目录

• 引
• 主要结果
  • 定理2，3
  • 定理4
  • 直观解释

Recovering Low-Rank Matrices From Few Coefficients In Any Basis-David Gross

引

依旧是一个重构矩阵的问题，这篇论文的符号有些奇怪，注意一下。假设有一个矩阵\(\rho \in \mathbb{R}^{n \times n}\),其秩为\(r \ll n\)。有一组基\(w_a, a=1,\ldots, n^2\)，是已知的。假设我们观测到的是，一组内积\(\{ (\rho, w_a) | a \in \Omega \}\)，其中\((\rho, w_a) = tr(\rho^{\dagger}w_a)\)，\(\rho^{\dagger}\)表示\(\rho\)的共轭转置。在这些条件下，我们是否能够从\(\{ (\rho, w_a) | a \in \Omega \}\)中恢复出\(\rho\)。

一些符号说明：
\(\|\rho\|_1\)为\(\rho\)的奇异值之和，即此为矩阵核范数。
\(\|\rho\|_2\)为\(\rho\)的F范数，而非一般符号代表的谱范数。
\(\|\rho\|\)为\(\rho\)的谱范数。

作者强调，这个问题，是可以办到的，不过其基需要满足一个coherence条件：

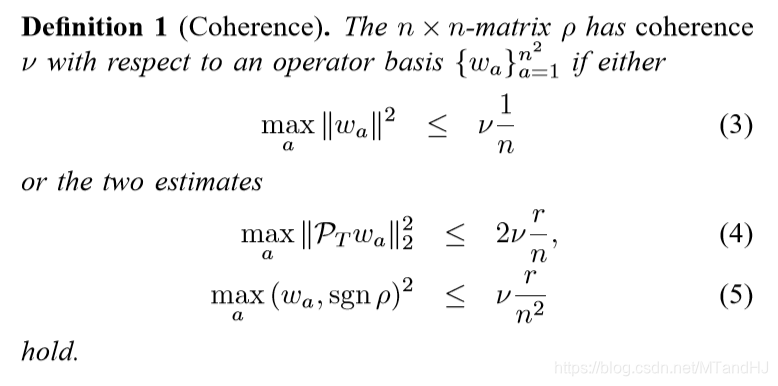
且\(\rho^{\dagger} = \rho\)，即\(\rho\)为酉矩阵（不过作者提到，似乎\(\rho\)即便不满足此条件，也可以通过一种转化来求解）。

主要结果

作者通过求解下述问题来恢复矩阵\(\rho\):

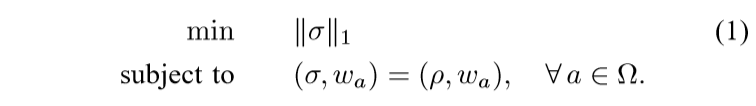
需要指明的一点是，如果\((\rho, w_a),a \in \Omega\)中大部分为0，那么想要恢复出\(\rho\)是非常困难的（因为这意味着我们可用的信息非常少）。

定理2，3

下为定理2，其中的标准基为：\(\{e_i e_j^{\dagger}\}_{i,j=1}^n\)，即仅有\(i\)行\(j\)列元素为1，其余均为0的\(n \times n\)矩阵所构成的基。

作者的结论更为一般，可以拓展到任意的基：

定理4

接下来还有定理4：

定理4针对的是一种特殊的基——Fourier-type基，介绍此的原因是，作者先证明此定理，再通过一些转换来证明定理3的。

直观解释

作者通过俩幅图，给出了一些直观的解释。

先来看(a)。我们可以将整个线性空间分成\(\Omega\)和\(\Omega^{\bot}\)。因为我们已有的信息是\(\Omega\)，问题(1)中满足约束的矩阵\(\sigma\)在空间中形成一个超平面，即图中的\(A\)，而我们所期望的\(\rho\)是其中的一点。

再来看(b)，因为我们希望的是\(\rho\)是问题(1)的最优解，最好还是唯一的。如果真的如此，那么\(B = \{\sigma | \|\sigma\|_1 \le \|\rho\|_1\}\)这个集合只能在平面\(A\)的上方或者下方，实际上，就是平面A是\(B\)的支撑超平面，其支撑点为\(\rho\)。

当然，这个性质并没有这么容易达成，其等价于要满足：

\[\|\rho + \Delta\|_1 \ge \|\rho\|_1 \]

对于\(A\)中任意的点\(\rho + \Delta \neq \rho\)成立。但是呢，直接证明是困难的，所以作者寻求一个对偶条件即下式：

\[\|\rho + \Delta\|_1 > \|\rho\|_1 + (Y, \Delta)，\Delta \neq 0 \]

关于某个\(Y\)成立，而且\(Y\)必须与超平面\(A\)垂直。这个\(Y\)能否找到，就是\(\rho\)能否恢复的关键。