生成函数

普通生成函数

基础知识

某个序列 \(a\) 的生成函数是一种形式幂级数，其每一项的系数可以提供关于这个序列的信息。

根据问题的不同，可以构造出不同形式的生成函数。

普通生成函数：

\(F(x)=\sum_{n\ge0}a_nx^n\)

\(a\) 既可以是有穷序列，也可以是无穷序列。

序列 \(a=\langle 1,2,3\rangle\) 的普通生成函数是 \(1+2x+3x^2\)。

序列 \(a=\langle 1,1,1,\cdots\rangle\) 的普通生成函数是 \(\sum_{n\ge 0}x^n\)。

序列 \(a=\langle 1,2,4,8,16,\cdots\rangle\) 的生成函数是 \(\sum_{n\ge 0}2^nx^n\)。

序列 \(a=\langle 1,3,5,7,9,\cdots\rangle\) 的生成函数是 \(\sum_{n\ge 0}(2n+1)x^n\)。

加减运算

\[\begin{aligned} {}F(x)\pm G(x)=&\sum_{i\ge0}a_ix^i\pm\sum_{j\ge0}b_jx^j\\ =&\sum_{n\ge0} (a_n\pm b_n)x^n \end{aligned} \]

因此 \(F(x)\pm G(x)\) 是序列 \(\langle a_n\pm b_n\rangle\) 的普通生成函数。

乘法运算（卷积）

\[\begin{aligned} {}F(x)G(x)=&\sum_{i\ge0}a_ix^i\sum_{j\ge0}b_jx^j\\ =&\sum_{n\ge0} x^n \sum_{i=0}^na_ib_{n-i} （令\ i+j=n） \end{aligned} \]

因此 \(F(x)G(x)\) 是序列
\(\langle \sum_{i=0}^n a_ib_{n-i} \rangle\) 的普通生成函数。

解决多重集组合数问题

问题：有 \(n\) 种物品，每种物品有 \(a_i\) 个，求取 \(m\) 个物品的的组合数。

首先构造普通生成函数。第 \(i\) 种物品的生成函数为 \((1+x^1+x^2+\dots x^{a_i})\)。指数即物品个数，系数即组合数。

举个例子，有 \(3\) 个物品，个数分别是 \(3,2,1\) 个，求取 \(4\) 个物品的方案数。

手动枚举可以得到 AAAB,AAAC,AABB,AABC,ABBC 五种方案。

生成函数求解如下：

\[\begin{aligned} {}&(1+x+x^2+x^3)(1+x+x^2)(1+x)\\ =&(1+x+x^2+x+x^2+x^3+x^2+x^3+x^4+x^3+x^4+x^5)(1+x)&\\ =&(1+2x+3x^2+3x^3+2x^4+x^5)(1+x)&\\ =&(1+x+2x+2x^2+3x^2+3x^3+3x^3+3x^4+2x^4+2x^5+x^5+x^6)&\\ =&(1+3x+5x^2+6x^3+5x^4+3x^5+x^6) \end{aligned} \]

指数为 \(4\) 的项系数为 \(5\)，所以有 \(5\) 个方案。

接下来给一道例题：

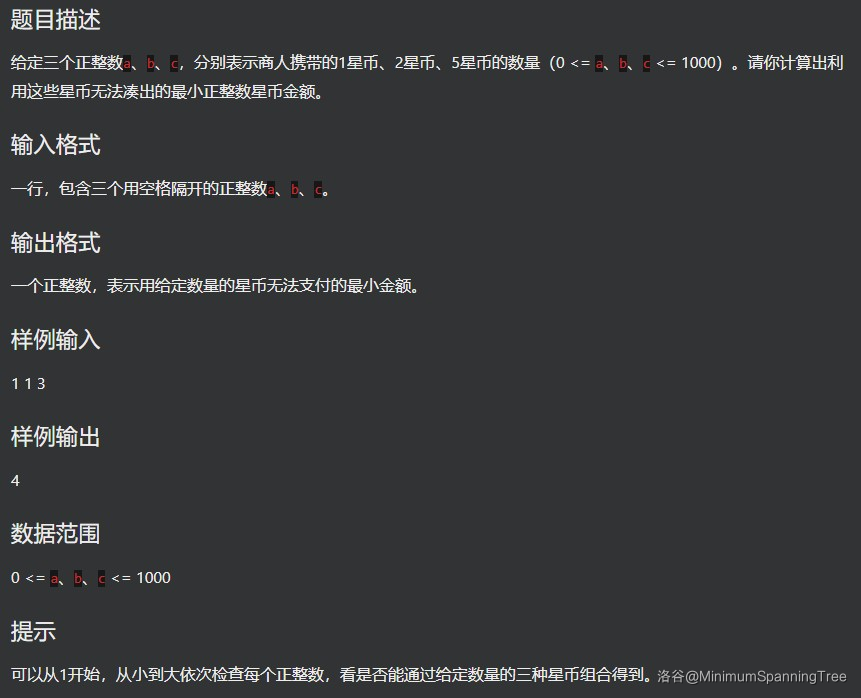
我们直接用上面的生成函数求解，第一个组合数为 \(0\) 的就是答案。

但是这题只需要知道是否可以组合出来，不需要知道组合数，所以节省空间，我们只需要用 bool 数组标记是否可行就可以了。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm> 
using namespace std;
const int N=10100,M=5;
int a[N],n,b[M],num[M]={0,1,2,5},a1[N];
int main()
{
	for(int i=1;i<=3;i++) scanf("%d",&b[i]);
	for(int i=0;i<=b[1];i++) a[i]=1;
	n=b[1]+b[2]*2+b[3]*5;
	for(int i=2;i<=3;i++)
	{
		for(int j=0;j<=n;j++)
		{
			if(!a[j]) continue;
			for(int k=0;k<=b[i]*num[i]&&j+k<=n;k+=num[i]) a1[j+k]+=a[j];
		}
		for(int j=0;j<=n;j++) a[j]+=a1[j],a1[j]=0;
	}
	for(int i=1;i<=n+1;i++)
	{
		if(!a[i])
		{
			printf("%d",i);
			break;
		}
	}
	return 0;
}

例题 2：

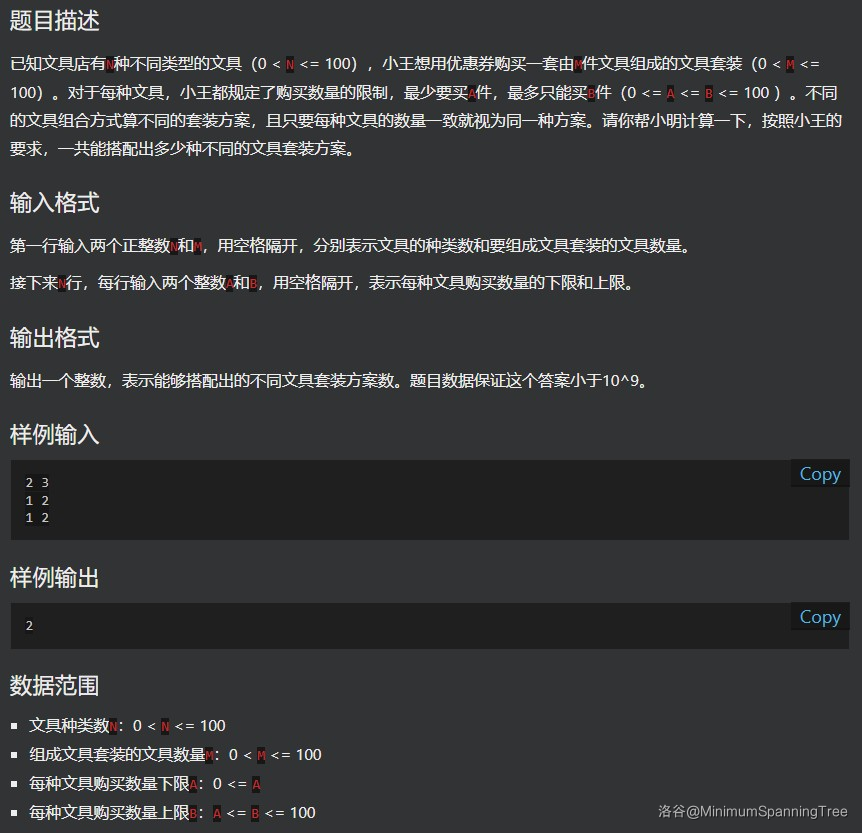
构造生成函数，对于第 \(i\) 个物品，生成函数为 \((x^{A^i}+\dots+x^{B_i})\)，\(x^M\) 即是我们要求的答案。

例如，选购的个数为 \([2,3],[0,2],[1,2]\)。

\[\begin{aligned} {}&(x^2+x^3)(1+x+x^2)(x+x^2)\\ =&(x^2+x^3+x^4+x^3+x^4+x^5)(x+x^2)&\\ =&(x^2+2x^3+2x^4+x^5)(x+x^2)&\\ =&(x^3+x^4+2x^4+2x^5+2x^5+2x^6)&\\ =&(x^3+3x^4+3x^5+2x^6) \end{aligned} \]

#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
const int N=1100;
int n,m,x,y;
ll a[N],a1[N];
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&x,&y);
		if(i==1)
		{
			for(int j=x;j<=y;j++) a[j]=1;
			continue;
		}
		for(int j=0;j<=m;j++)
		{
			for(int k=x;k<=y;k++) a1[j+k]+=a[j];
		}
		for(int j=0;j<=m;j++) a[j]=a1[j],a1[j]=0;
	}
	printf("%lld",a[m]);
	return 0;
}