洛谷 P2017 [USACO09DEC] Dizzy Cows G 题解

题目链接

感觉挺思维的图论好题，可惜没有自己想出来。

本题的难点在于，我们不知道无向边定成某一个方向会不会造成与其他边相连成环。于是考虑先不看无向边，对有向边进行观察。考虑最坏的情况，若干个有向边连成如下的状态：

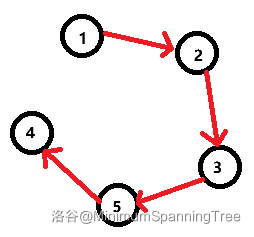
这时如果 \(1\) 和 \(4\) 之间有一条无向边，那么只能是 1->4。我们把上图看作一条链，这种情况。必须是要把起始点连向结束点的。再考虑拓扑排序，结束起始点的拓扑序一定是比结束点的拓扑序小的，所以只需要知道两点的拓扑序即可确定无向边的方向。

对于代码实现，我们只需要先看只有有向边的图，进行拓扑排序存储每个点的拓扑序，再边输入边利用两个端点的拓扑序判断无向边方向即可。

正确性证明：为什么前面在摆放了一些无向边后，后面的无向边仍然用只有有向边的拓扑序来判断方向？

一开始我认为每次定向并加入无向边之后，需要重新计算拓扑序，所以并不能理解并严格证明这个方法的正确性。实际上这个可以用拓扑排序的底层原理来证明。我们知道一个图可以进行拓扑排序，说明它必须是 DAG，就已经满足了无环。又因为拓扑排序不能有环的原因是一个点层层递进形成如上图的样子，说明 \(1\) 是必须要在 \(4\) 前面的，但是如果加一条 4->1 的话 \(1\) 就需要在 \(4\) 前面，自相矛盾。又因为这题的目的是无环，加入定向后的无向边不会产生环，自然也不会出现与前面矛盾的地方，就不需要重新计算拓扑序。或者不那么抽象一点地证明，在最坏情况（上图）下，从拓扑排序的视角来看，这条边加了和没加一样。因为拓扑排序的本质是“A 要放在 B 的前面”，我们新加入的 1->4 相当于我们要让 \(1\) 放在 \(4\) 前面，但是已有的边 1->2->3->4，是不是已经间接地要求了 \(1\) 要放在 \(4\) 的前面，所以证毕。

#include<iostream>
#include<cstdio>
using namespace std;
const int N=100100;
int n,m1,m2,u,v,t[N],d[N],q[N],l=1,r,k,b[N];
struct node
{
	int id,last;
}a[N];
void add(int a1,int a2)
{
	a[++k].id=a2;
	a[k].last=t[a1];
	t[a1]=k;
}
int main()
{
	scanf("%d%d%d",&n,&m1,&m2);
	while(m1--)//先只看有向边 
	{
		scanf("%d%d",&u,&v);
		add(u,v);
		d[v]++;
	}
	for(int i=1;i<=n;i++) 
	{
		if(!d[i]) q[++r]=i;
	}
	while(l<=r)//拓扑排序 
	{
		b[q[l]]=l;
		for(int i=t[q[l]];i;i=a[i].last)
		{
			d[a[i].id]--;
			if(d[a[i].id]==0) q[++r]=a[i].id;
		}
		l++;
	}
	while(m2--)//对无向边进行定向 
	{
		scanf("%d%d",&u,&v);
		if(b[u]>b[v]) swap(u,v);
		printf("%d %d\n",u,v);
	}
	return 0;
}