KMP

\(\text{KMP}\) 的原理

\(\text{KMP}\) 算法是一种改进的字符串匹配算法，它的核心是利用匹配失败后的信息尽量减少匹配串和主串的匹配次数以达到快速匹配的目的。

时间复杂度：\(O(m+n)\)。

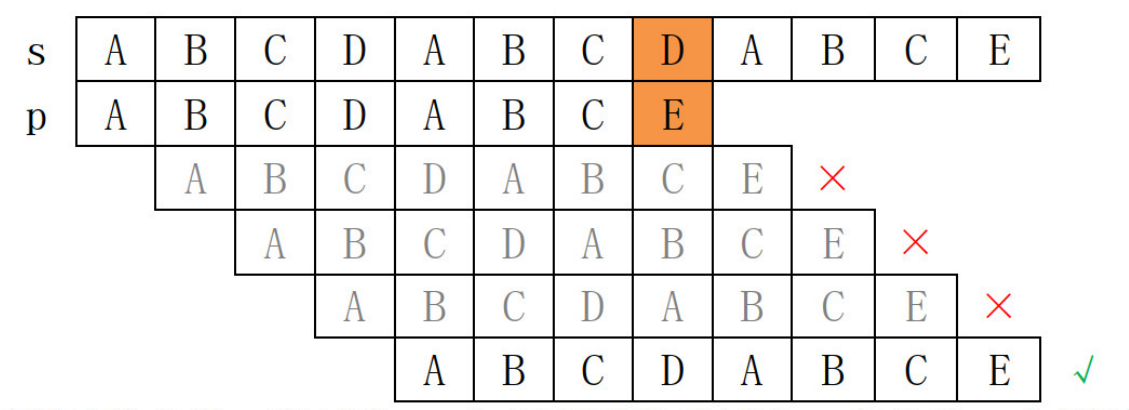
例如下图所示，要求匹配主串 \(s\) 和匹配串 \(p\)，并求出匹配多少次。

如果采用暴力枚举，时间复杂度 \(O(n^2)\)，如何优化？

考虑是否能直接跳过中间三次必定失败的匹配。

第一次匹配，发现 \(s_8\not=p_8\) 时，观察 \(p\) 的前 \(7\) 个字符可以发现，\(p\) 有前 \(3\) 个前缀子串和后 \(3\) 个后缀字串完全匹配，可以利用这个性质，直接跳过中间的 \(3\) 次无效匹配。

前缀函数

我们用 \(a\) 数组来表示前缀函数。\(a_i\) 表示字符串 \(p\) 中前 \(i\) 个字符的最大相同前缀和后缀的值。（不包含自身。）

如何高效求前缀函数？

当 \(s_{i+1}\not=p_{j+1}\)，通过 \(j=a_j\) 回跳直到 \(s_{i+1}=p_{j+1}\)，则 \(a_{i+1}=j\)。

for(int i=1,j=0;i<len2;i++)
{
	while(j&&s2[i+1]!=s2[j+1]) j=a[j];
	if(s2[i+1]==s2[j+1]) j++;
	a[i+1]=j;
}

时间复杂度 \(O(n)\)。

\(\text{KMP}\) 模板题

P3375 【模板】KMP

有一点需要注意，字符串的下标最好从 \(1\) 开始，不然写起来容易错。

首先先求一遍前缀函数，求解方法前文已经讲过，不再赘述。

接下来对两个字符串进行匹配。从 \(1\) 开始匹配，如果匹配失败，\(j\) 不断通过前缀函数回跳，接下来 \(s2\) 的前缀跳到对应 \(s1\) 前缀处，就可以跳过中间的无效匹配。当 \(j\) 和 \(s2\) 的长度相等时，说明匹配成功。

#include<iostream>
#include<cstdio>
using namespace std; 
const int N=1e6+100;
int len1,len2,a[N];
string s1,s2;
int main()
{
	cin>>s1>>s2;
	len1=s1.size(),len2=s2.size();
	s1=" "+s1,s2=" "+s2;
	for(int i=1,j=0;i<len2;i++)
	{
		while(j&&s2[i+1]!=s2[j+1]) j=a[j];
		if(s2[i+1]==s2[j+1]) j++;
		a[i+1]=j;
	}
	for(int i=0,j=0;i<len1;i++)
	{
		while(j&&s1[i+1]!=s2[j+1]) j=a[j];
		if(s1[i+1]==s2[j+1]) j++;
		if(j==len2) printf("%d\n",i-len2+2);
	} 
	for(int i=1;i<=len2;i++) printf("%d ",a[i]);
	return 0;
}

一些好题

P3435 [POI2006] OKR-Periods of Words 考察对前缀函数的理解。