【leetcode_C++_二叉树_day11】前序遍历&&中序遍历&&后序遍历的递归法和迭代法

二叉树知识补充

二叉树的种类：满二叉树和完全二叉树

二叉搜索树：二叉搜索树是一个有序树。

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树

下面这两棵树都是搜索树

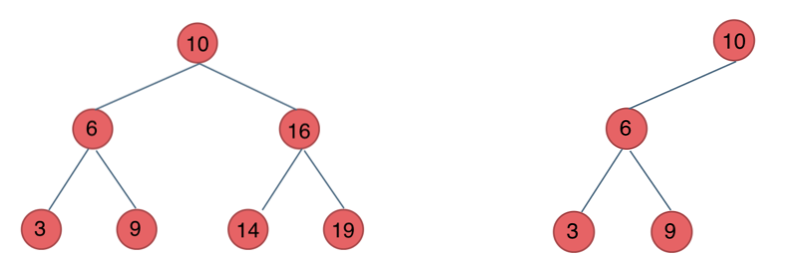
平衡二叉搜索树（AVL):它是一棵空树，或者左右子树高度差的绝对值小于等于1.

**C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树**，所以map、set的增删操作时间时间复杂度是logn，注意我这里没有说unordered_map、unordered_set，unordered_map、unordered_map底层实现是哈希表。

二叉树的存储方式：链式存储/顺序存储

二叉树主要有两种遍历方式：

1. 深度优先遍历：先往深走，遇到叶子节点再往回走。
2. 广度优先遍历：一层一层的去遍历

• 深度优先遍历（一般选用递归法）

  • 前序遍历（递归法，迭代法）
  • 中序遍历（递归法，迭代法）
  • 后序遍历（递归法，迭代法）

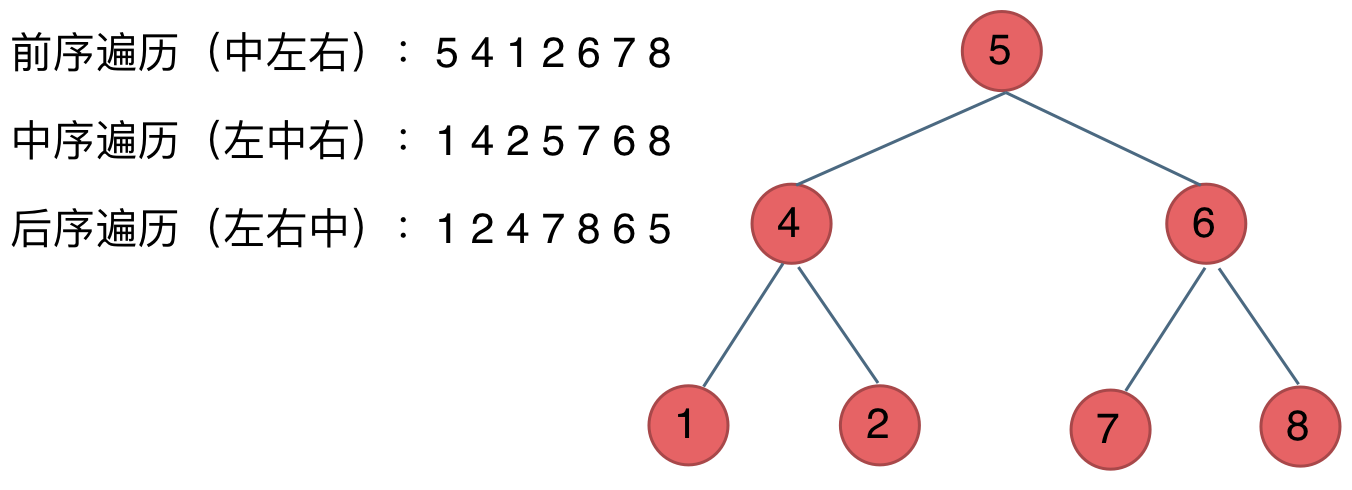
之前我们讲栈与队列的时候，就说过栈其实就是递归的一种是实现结构，也就说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的。

• 广度优先遍历

  • 层次遍历（迭代法）

  而广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出的结构，才能一层一层的来遍历二叉树。

  二叉树的结构定义

  struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode(int x) : val(x), left(NULL), right(NULL) {}
  };
  

  在现场面试的时候 面试官可能要求手写代码，所以数据结构的定义以及简单逻辑的代码一定要锻炼白纸写出来。

1. 二叉树的递归遍历

递归三要素：

a) 确定递归函数的参数和返回值

b) 确定终止条件

c) 确定单层递归的逻辑

以前序遍历为例：

另外定义一个函数

 void traversal(*)

1. 确定递归函数的参数和返回值：因为要打印出前序遍历节点的数值，所以参数里需要传入vector在放节点的数值，除了这一点就不需要在处理什么数据了也不需要有返回值，所以递归函数返回类型就是void，代码如下：

void traversal(TreeNode* cur, vector<int>& vec)

2. 确定终止条件：在递归的过程中，如何算是递归结束了呢，当然是当前遍历的节点是空了，那么本层递归就要要结束了，所以如果当前遍历的这个节点是空，就直接return，代码如下：

if (cur == NULL) return;

3. 确定单层递归的逻辑：前序遍历是中左右的循序，所以在单层递归的逻辑，是要先取中节点的数值，代码如下：

vec.push_back(cur->val);    // 中
traversal(cur->left, vec);  // 左
traversal(cur->right, vec); // 右

单层递归的逻辑就是按照中左右的顺序来处理的，这样二叉树的前序遍历，基本就写完了。

后序遍历和中序遍历只需要改变单层递归的逻辑就可以了。

首先是树的结构：

struct TreeNode{
  int val;
  TreeNode *left;
  TreeNode *right;
  TreeNode(int x):val(x),left(NULL),right(NULL){}
};

前序遍历：

class Solution{
public:
//前序遍历：中左右
  void traversal(TreeNode* cur, vector<int>& vec){//cur:根结点，vec:存储数据
    if(cur==NULL) return;//终止条件
    vec.push_back(cur->val);//中
    traversal(cur->left,vec);//左
    traversal(cur->right,vec);//右
  }
  vector<int> preorderTraversal(TreeNode* root){
    vector<int> result;
    traversal(root,result);
    return result;
  }
}

中序遍历：

//中序遍历：左中右
  void traversal(TreeNode* cur, vector<int>& vec){//cur:根结点，vec:存储数据
    if(cur==NULL) return;//终止条件    
    traversal(cur->left,vec);//左
    vec.push_back(cur->val);//中
    traversal(cur->right,vec);//右
  }

后序遍历：

  void traversal(TreeNode* cur, vector<int>& vec){//cur:根结点，vec:存储数据
    if(cur==NULL) return;//终止条件
    traversal(cur->left,vec);//左
    traversal(cur->right,vec);//右
    vec.push_back(cur->val);//中
  }

2. 二叉树的迭代遍历

迭代法不是非递归的方式。

采用的是堆栈的方式。

1. 定一个堆栈，一个存放结果的数组
2. 先把头节点压入栈中，然后讲右孩子加入栈，再加入左孩子。之所以反过来，是因为这样出栈的时候就是先出左孩子再出右孩子。
   

前序遍历：

class Solution {
public:

    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;//定义栈
        vector<int> result;//定义存放结果的数组
        if(root==NULL) return result;//确保不是空节点

        //前序遍历；中左右
        st.push(root);//把头节点压入栈中
        while(!st.empty())
        {
            TreeNode* node = st.top();//把头节点弹出，中
            st.pop();
            result.push_back(node->val);//往result中push进结果
            //和前序访问的顺序颠倒，先放右孩子再放左孩子
            if(node->right) st.push(node->right);//先放右孩子（空结点不如栈）
            if(node->left) st.push(node->left);//再放左孩子（空结点不如栈）
        }
        return result;
    }
};

后序遍历只要把前序遍历的顺序颠倒，再反转result数组就可以了

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;//定义一个堆栈
        vector<int> result;//定义一个数组
        if(root==NULL) return result;
        //后序遍历：左右中
        st.push(root);//把根结点压入堆栈中
        while(!st.empty())
        {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if(node->left) st.push(node->left);//先入左孩子入栈
            if(node->right) st.push(node->right);//再右孩子入栈
        }
        reverse(result.begin(),result.end());
        return result;
    }
};

中序遍历不一样

1. 处理：将元素放进result数组中
2. 访问：遍历节点

分析一下为什么刚刚写的前序遍历的代码，不能和中序遍历通用呢，因为前序遍历的顺序是中左右，先访问的元素是中间节点，要处理的元素也是中间节点，所以刚刚才能写出相对简洁的代码，因为要访问的元素和要处理的元素顺序是一致的，都是中间节点。

那么再看看中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。

那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

动画如下：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;//堆栈st，堆栈用来处理节点元素
        TreeNode* cur = root;//指针cur，指针用来访问节点
        while(cur!=NULL||!st.empty())//如果指针不为NULL且堆栈不为空
        {
            if(cur!=NULL)//指针用来访问节点，一直访问到左子树的最底层
            {
                st.push(cur);//讲访问的节点放进栈
                cur=cur->left;//左
            }
            else//到达了左子树的最底层后
            {
                cur=st.top();// 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
                st.pop();
                result.push_back(cur->val);//把弹出的结果压入堆栈
                cur=cur->right;//右
            }
        }
        return result;
    }
};

3.二叉树的统一迭代法

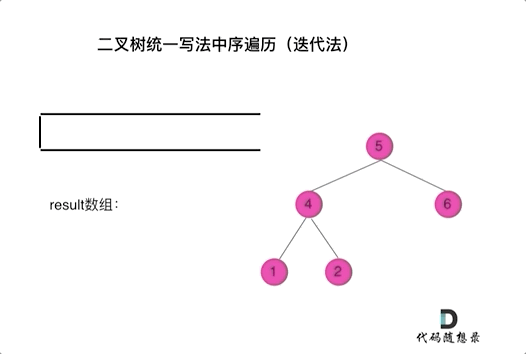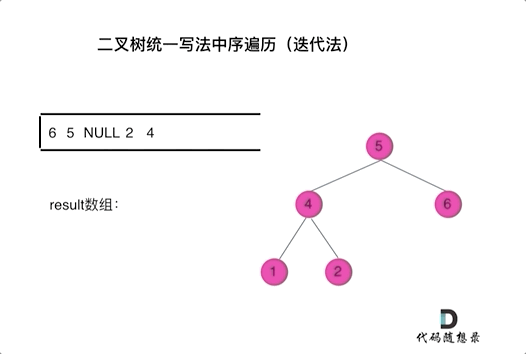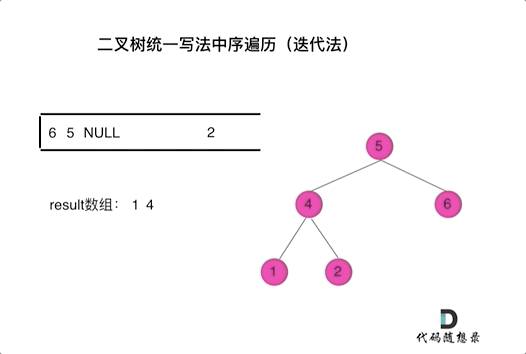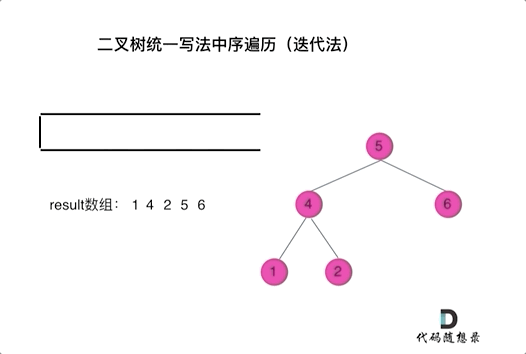
迭代法很难写出如递归法一样只要稍稍改一下节点就可以的结构，但是我们可以通过标记法实现迭代法的统一风格代码。

以中序为例：

使用栈的话，无法同时解决访问节点（遍历节点）和处理节点（将元素放进结果）不一致的情况。

那我们就将访问的节点放入栈中，把要处理的节点也放入栈中，但是要做标记。标记的方法就是把要处理的节点放入栈后，紧接着放一个空指针作为标记。

空指针是一个标志，标志着这是一个需要处理的节点。

统一迭代法就是在迭代法的基础上加了空指针标志，并且加了判断node是否出现控制的if语句。这种方法只需要调整压入顺序即可实现三种遍历。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        //中序：左中右
        //为了弹出的时候顺序正确，压入的时候先压入右孩子，再压入左孩子
        if(root!=NULL) st.push(root);
        while(!st.empty())
        {
            TreeNode *node =st.top();
            if(node!=NULL)
            {
                st.pop();//将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                if(node->right) st.push(node->right);//添加右节点（空节点不如栈）

                st.push(node);//添加中节点
                st.push(NULL);//中节点访问过，但是还没有处理，加入空节点作为标记

                if(node->left) st.push(node->left);//添加左节点（空节点不入栈）
            }
            else//只有遇到空节点的时候，才将下一个节点放进结果集
            {
                st.pop();//将空节点弹出
                node=st.top();//重新取出栈中元素
                st.pop();
                result.push_back(node->val);//加入到结果集
            }
        }

        return result;
    }
};

前序遍历：

迭代法前序遍历代码如下： (注意此时我们和中序遍历相比仅仅改变了两行代码的顺序)

class Solution {
public:

    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;//定义栈
        vector<int> result;//定义存放结果的数组
        if(root==NULL) return result;//确保不是空节点

        //前序遍历；中左右
        //倒过来压入：右左中
        st.push(root);//把头节点压入栈中
        while(!st.empty())
        {
            TreeNode* node=st.top();
            if(node!=NULL)
            {
                st.pop();
                if(node->right) st.push(node->right);
                if(node->left) st.push(node->left);
                st.push(node);
                st.push(NULL);
            }
            else
            {
                st.pop();
                node=st.top();
                st.pop();
                result.push_back(node->val);
            }

        }
        return result;
    }
};

后序遍历：

后续遍历代码如下： (注意此时我们和中序遍历相比仅仅改变了两行代码的顺序)

class Solution {
public:

    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;//定义栈
        vector<int> result;//定义存放结果的数组
        if(root==NULL) return result;//确保不是空节点

        //后序遍历；左右中
        //倒过来压入：中右左
        st.push(root);//把头节点压入栈中
        while(!st.empty())
        {
            TreeNode* node=st.top();
            if(node!=NULL)
            {
                st.pop();
                st.push(node);
                st.push(NULL);
                if(node->right) st.push(node->right);
                if(node->left) st.push(node->left);
            }
            else
            {
                st.pop();
                node=st.top();
                st.pop();
                result.push_back(node->val);
            }

        }
        return result;
    }
};