这一章就是将我们自己定义的一些逻辑集成一个函数-----封装(严格意义下后续说的 “类” 才能称为封装)让程序模块化,有利于数据共享,节省开发时间,便于管理和增加程序的可靠性,具体知识可以关注我的C++基础专栏
后续会更新 请持续关注奥!
这一章会收录很多关于函数的练习题
网易云音乐链接 : -------------点我呀-------------.(被1分27秒开始的音乐沦陷了)
1. 定义一个函数:求两个整数的最大值。
要求:
(1)函数名:max
(2)函数的参数:x和y
(3)函数返回值的类型:整型
(4)函数返回值:x和y中较大者
(5)函数体:求x和y中的较大者
程序:
#include<iostream>
using namespace std;
int max(int x,int y)
{
int z=(x>y?x:y);
return z;
}
int main()
{
int a,b,m;
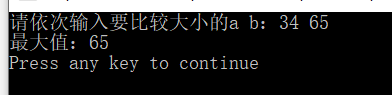
cout<<"请依次输入要比较大小的a b:";
cin>>a;
cin>>b;
m = max(a,b);
cout<<"最大值:"<<m<<endl;
return 0;
}
运行结果:
2. 利用自定义的求绝对值函数和系统提供的求绝对值标准函数分别求数的绝对值并输出。
要求:
(1)自定义求一个数绝对值函数abs。
(2)使用系统库中的求绝对值函数。
程序:
#include<iostream>
#include<cmath>
using namespace std;
int abs(int x);
int main()
{
int a;
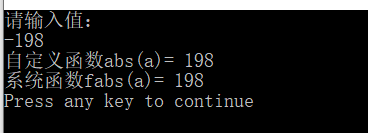
cout<<"请输入值:"<<endl;
cin>>a;
cout<<"自定义函数abs(a)= "<<abs(a)<<endl;
cout<<"系统函数fabs(a)= "<<fabs(a)<<endl;
return 0;
}
int abs(int x)
{
x = (x<0?-x:x);
return x;
}
运行结果:
3. 利用求最大值函数,求三个数的最大值。
要求:
使用自己定义的求最大值函数max()。
程序:
#include<iostream>
#include<cmath>
using namespace std;
int max(int x, int y, int z);
int main()
{
int a,b,c;
cout<<"请依次输入要比较的三个数:";
cin>>a;
cin>>b;
cin>>c;
cout<<"这三个数的最大值为:"<<max(a,b,c)<<endl;
return 0;
}
int max(int x, int y, int z)
{
if(x>=y && x>=z)
return x;
else if(y>=z)
return y;
else return z;
}
运行结果:
4. 编写两个函数,分别实现对10个数求和及平均值。
提示与分析:
在求和函数中需要接收10个数然后求和,因此使用含有10个元素的数组作为函数形参,在函数体内对数组元素求和;在求平均值函数中只需接收10个数的和然后求平均值,因此使用暂存10个数和一个函数形参。
程序:
#include<iostream>
#include<cmath>
#include <cstdlib>
#include <ctime>
using namespace std;
int arrayValue(int array[10]);
void arrayPrint(int array[10]);
int Sum(int array[10]);
double Average(double s);
int main()
{
int array[10];
double sum;
double average;
arrayValue(array);
arrayPrint(array);
sum = Sum(array);
average = Average(sum);
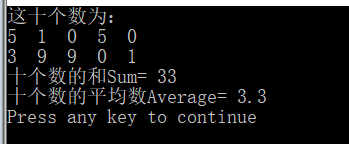
cout<<"十个数的和Sum= "<<sum<<endl;
cout<<"十个数的平均数Average= "<<average<<endl;
return 0;
}
//数组压值
int arrayValue(int array[10])
{
srand((int)time(0));
for(int i=0;i<10;i++)
{
array[i] = rand()%10;
}
return 0;
}
//数组值打印
void arrayPrint(int array[10])
{
int count = 0;
cout<<"这十个数为:"<<endl;
for(int i=0;i<10;i++)
{
cout<<array[i]<<" ";
count++;
if(0==count%5)
cout<<endl;
}
}
//数组求和
int Sum(int array[10])
{
int sum=0;
for(int i=0;i<10;i++)
sum += array[i];
return sum;
}
//求平均值
double Average(double s)
{
return (s/10);
}
运行结果:
5. 利用函数递归求s=1+2+3……+n 。
递归问题的提示与分析:
将原问题分解为一个新问题,而新问题又用到了原问题的解法,但是,新问题又是原问题简化的子问题,依次分解下去,直到最终分解出来的新问题是一个已知解的问题。
程序:
#include<iostream>
using namespace std;
int recurSum(int i);
int main()
{
int sum=0;
int n;
cout<<"请输入n值:";
cin>>n;
sum = recurSum(n);
printf("%d以内的和为",n);
cout<<"SUM = "<<sum<<endl;
return 0;
}
//用递归法求1-n数的和
int recurSum(int n)
{
int result;
if(n<=0)
result=0;
else if(n==1)
result=1;
else
result=recurSum(n-1)+n;
return result;
}
运行结果:
-------------------------------------作业练习-------------------------------------
1. 设计一个程序,要求输入三个整数,能求出其中的最大数并输出。程序中必须用函数实现求两数中大数的功能。
程序:
#include<iostream>
#include<cmath>
using namespace std;
int max(int x, int y, int z);
int main()
{
int a,b,c;
cout<<"请依次输入要比较的三个数:";
cin>>a;
cin>>b;
cin>>c;
cout<<"这三个数的最大值为:"<<max(a,b,c)<<endl;
return 0;
}
int max(int x, int y, int z)
{
if(x>=y && x>=z)
return x;
else if(y>=z)
return y;
else return z;
}
运行结果:
2. 设计一个程序,求出100—200之间的所有素数,要求每行输出5个素数。判断一个整数是否为素数用一个函数来实现。
程序:
#include<iostream>
#include<cmath> //sqrt(a)
using namespace std;
bool isPrime(int a);
int main()
{
int i,count=0;
cout<<"100-200间的素数为:"<<endl;
for(i=101;i<200;i++)
{
if(isPrime(i))
{
cout<<i<<" ";
count++;
if(0==count%5) //五个数为一行输出
cout<<endl;
}
}
cout<<endl;
return 0;
}
//判断一个整数是否为素数,返回类型为bool型
bool isPrime(int a)
{
int j = 2;
for(j;j<sqrt(a)+1;j++) //sqrt(a)优化算法
{
if(0 == a%j)
return false; //如果是合数,返回false
}
return true; //如果是素数,返回true
}
运行结果:
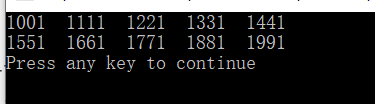
3. 回文数是指其各位数字左右对称的整数,如12321是回文数。定义一个判断回文数的函数,并输出1000—2000之间的所有回文数。
程序:
//定义一个判断回文数的函数,并输出1000---2000之间的所有回文数。
#include<iostream>
#include<cmath>
using namespace std;
bool isPalindrome(int a);
int main()
{
int i, count=0;
for(i=1000; i<2000; i++)
{
if(isPalindrome(i))
{
count++;
cout<<i<<" ";
if(0 == count%5)
cout<<endl;
}
}
return 0;
}
//判断是否为回文数
bool isPalindrome(int value)
{
int tmp = 0;
int index = value;
while(index)
{
tmp = tmp*10 + index%10;
index = index/10;
}
if(value==tmp)
return true;
else
return false;
}
运行结果:
4. 用函数实现求两正整数的最大公约数的功能,并在主函数中调用该函数求出两正整数的最小公倍数。
提示分析:
用最大公约数跟最小公倍数的关系编写程序
程序:
#include<iostream>
#include<cmath>
using namespace std;
int commonMultiple(int x, int y);
int main()
{
int x,y,multiple;
cout<<"请输入两个正整数:";
cin>>x;
cin>>y;
multiple = commonMultiple(x,y);
cout<<"两个整数的最小公倍数是: "<<multiple<<endl;
return 0;
}
//辗转相除法求最大公约数
int commonDivisor(int x, int y)
{
int tmp;
//比较两个数的大小,值大的数为a,值小的数为b
if (x < y) {
tmp = x;
x = y;
y = tmp;
}
//求余
while (y != 0) {
tmp = x % y;
x = y;
y = tmp;
}
return x;
}
//最小公倍数
int commonMultiple(int x, int y)
{
int commonDivisor(int x, int y);
int tmp=0;
tmp = commonDivisor(x,y);
return (x*y/tmp);
}
运行结果:
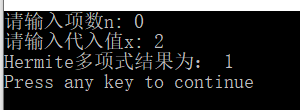
5. 用递归函数实现Hermite多项式求值,当x>1时,Hermite多项式定义为:
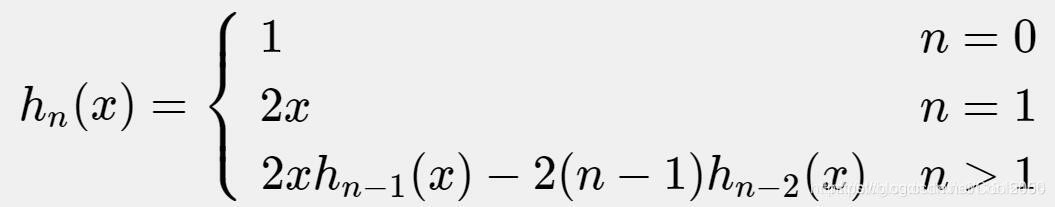 程序:
程序:
#include<iostream>
#include<cmath>
using namespace std;
int Hermite(int item, int value);
int main()
{
int item,value,result;
cout<<"请输入项数n: ";
cin>>item;
cout<<"请输入代入值x: ";
cin>>value;
result = Hermite(item,value);
cout<<"Hermite多项式结果为: "<<result<<endl;
return 0;
}
int Hermite(int item, int value)
{
int temp;
if(0 == item)
temp = 1;
if(1 == item)
temp = 2*value;
if(item>1)
temp = 2*value*(Hermite(item-1,value))-2*(item-1)*(Hermite(item-2,value));
return temp;
}
运行结果:
n=0
n=1
n>1
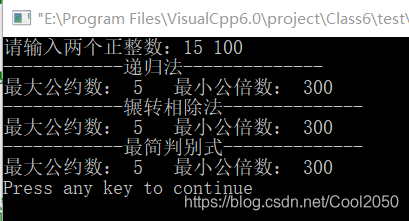
6. 写两个函数分别实现求两正整数的最大公约数和最小公倍数的功能,并在主函数中调用这两个函数求出两正整数的最大公约数和最小公倍数。
程序:
#include<iostream>
#include<cmath>
using namespace std;
int commonMultiple(int x, int y);
int commonDivisor(int x, int y); //方法一
int lcm(int a, int b);
int gcd(int a, int b); //方法二
int cd(int x, int y);
int cm(int x, int y); //方法三
int main()
{
int x,y,multiple,divisor;
cout<<"请输入两个正整数:";
cin>>x;
cin>>y;
cout<<"------------递归法--------------\n";
divisor = gcd(x,y); //最大公约数
multiple = lcm(x,y); //最小公倍数
cout<<"最大公约数: "<<divisor<<" 最小公倍数: "<<multiple<<endl;
cout<<"------------辗转相除法--------------\n";
divisor = commonDivisor(x, y);
multiple = commonMultiple(x, y);
cout<<"最大公约数: "<<divisor<<" 最小公倍数: "<<multiple<<endl;
cout<<"------------最简判别式--------------\n";
divisor = cd(x,y);
multiple = cm(x,y);
cout<<"最大公约数: "<<divisor<<" 最小公倍数: "<<multiple<<endl;
return 0;
}
//-----递归法------
//最大公约数
int gcd(int a, int b)
{
return a % b ? gcd(b, a % b) : b;
}
//最小公倍数
int lcm(int a, int b)
{
return a * b / gcd(a, b);
}
//辗转相除法求最大公约数
int commonDivisor(int x, int y)
{
int tmp;
//比较两个数的大小,值大的数为a,值小的数为b
if (x < y) {
tmp = x;
x = y;
y = tmp;
}
//求余
while (y != 0) {
tmp = x % y;
x = y;
y = tmp;
}
return x;
}
//最小公倍数
int commonMultiple(int x, int y)
{
int commonDivisor(int x, int y);
int tmp=0;
tmp = commonDivisor(x,y);
return (x*y/tmp);
}
//最简判别式求公约数
int cd(int x, int y)
{
int i;
for(i=x;i>=1;i--)
if(0==x%i&&0==y%i)
return i;
}
//最小公倍数
int cm(int x, int y)
{
int cd(int x, int y);
int tmp=0;
tmp = cd(x,y);
return (x*y/tmp);
}
运行结果:











 浙公网安备 33010602011771号
浙公网安备 33010602011771号