【题目合集】反比例函数 | 图形存在性判断

【题目合集】反比例函数 | 图形存在性判断

1.（2023 秋·盐城月考）

如图，点 \(A\) 在双曲线 \(y=\frac{k}{x} \ (k \neq 0)\) 的第一象限的图象上，\(AB\) 垂直于 \(y\) 轴于点 \(B\)，点 \(C\) 在 \(x\) 轴的正半轴上，且 \(OC=3AB\)，点 \(E\) 在线段 \(AC\) 上，且 \(AE=3EC\)，点 \(D\) 为 \(OB\) 的中点，若 \(\triangle ADE\) 的面积为 \(3\)，求 \(k\) 值。

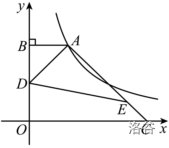
设 \(AB=a\)，则 \(OC=3a,OB=\frac{k}{a},BD=DO=\frac{k}{2a}\)。

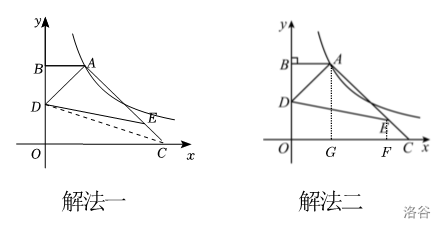
【解法一】面积法

连接 \(DC\)，可知：

\[S_{梯形ABOC}=S_{\triangle ABD}+S_{\triangle ADC}+S_{\triangle DOC} \]

所以 \(S_{\triangle ABD}=\frac{1}{2} \cdot a \cdot \frac{k}{2a}=\frac{k}{4}\)。

\(S_{\triangle DOC }=\frac{1}{2} \cdot 3a \cdot \frac{k}{2a}=\frac{3k}{4}\)。

又因为 \(\triangle AOE,\triangle DEC\) 同高，且 \(AE=3EC,S_{\triangle ADE}=3\)。

所以 \(S_{\triangle ADC}=4\)。

又因为 \(S_{梯形 ABOC}=\frac{1}{2}(a+3a)\frac{k}{a}=2k\)。

所以：

\[\frac{3k}{4}+\frac{k}{4}+4=2k \]

解得 \(k=4\)。

【解法一】面积法、相似

如图，作 \(AG,EF \perp x\) 轴。

可知 \(\triangle AGC \sim \triangle EFC\)。

同理可得 \(EC=\frac{k}{4a},FG=\frac{3k}{2},GC=\frac{k}{2}\)。

所以，有

\[S_{\triangle ADE} = S_{梯形 AOBC}-(S_{\triangle ABD} + S_{\triangle EGC} + S_{梯形 DOGE}) \]

可列方程：

\[\frac{1}{2} \times \frac{k}{2a} \cdot a - \left[ \left(\frac{k}{2a} + \frac{k}{4a} \right) \cdot \frac{5a}{2} + \frac{k}{4} + \frac{k}{4a} \times \frac{1}{2}\right] = 3 \]

解得 \(k=4\)。

2.（2023·顺德区三模）等积转化

如图，平行于 \(y\) 轴的直尺（部分）与反比例函数 \(y=\frac{m}{x}(x>0)\) 的图象交于 \(A,C\) 两点与 \(x\) 轴交于 \(B,D\) 两点，连接 \(AC\)，点 \(A,B\) 对应直尺上的刻度分别为 \(5,2\)，直尺的宽度 \(BD=2,S_{\triangle AOC}=5\)，求点 \(C\) 的坐标。

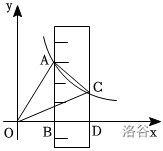
由题意得 \(A(3,\frac{m}{3})\)，则 \(B(\frac{m}{3},0)\)。

所以 \(D(\frac{m}{3}+2,0)\)，将 \(x_C\) 代入 \(y=\frac{m}{x}\)，得 \(C(\frac{m}{3}+2,\frac{3m}{m+6})\)。

所以 \(CD=\frac{3m}{m+6}\)。

有如下定理：\(S_{\triangle AOC}=S_{梯形 ABDC}\)。

因为根据反比例函数的性质，\(S_{\triangle AOB}=S_{\triangle COD}=\frac{|m|}{2}\)。

减去公共部分就会发现，有一个三角形和一个梯形面积相等。所以直接转化面积。所以：

\[\frac{1}{2} \cdot 2 \left( \frac{3m}{m+6} +3 \right) =5 \]

解得 \(m=12\)。直接代入，得 \(C(6,2)\)。

3.（2024·顺河区校级一模）

如图，一次函数 \(y=ax+b\) 的图象与反比例函数 \(y=\frac{k}{x}\) 的图象交于第一象限 \(C(1,4),D(4,m)\) 两点，与坐标轴交于 \(A\)、\(B\) 两点, 连接 \(OC,OD\)（\(O\) 是坐标原点）。

• 求一次函数与反比例函数的解析式。

• 将直线 \(AB\) 向下平移多少个单位长度，直线与反比例函数图象只有一个交点？

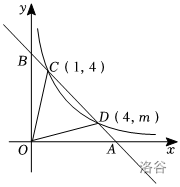
第一问直接跳过，得 \(y=\frac{4}{x},l_{AB}:y=-x+5\)。

对于第二问，设 \(l_{AB}':y=-x+5-m\)。

\( \left\{\begin{matrix} y=\frac{4}{x}\\ l_{AB}:y=-x+5 \end{matrix}\right. \) 得 \(x^2-(5-m)x+4=0\)。

令 \(\Delta=0\)，解得 \(m_1=9,m_2=1\)。

4.（2025·市中区一模）

如图 \(1\)，在平面直角坐标系中，矩形 \(OCBA\) 的顶点 \(C,A\) 分别在 \(x\) 轴和 \(y\) 轴的正半轴上，反比例函数 \(y=\frac{k}{x}\) 的图象与 \(AB,BC\) 分别交点 \(D,E\)，且顶点 \(B\) 的坐标为 \((6,3),BD=2\)。

• 求反比例函数 \(y=\frac{k}{x}\) 的表达式及 \(E\) 点坐标;

• 如图 \(2\)，连接 \(DE,AC\)，试判断 \(D E\) 与 \(AC\) 的数量和位置关系，并说明理由。

• 如图 \(3\)，连接 \(AE\)，在反比例函数 \(y=\frac{k}{x}\) 的图象上是否存在点 \(F\)，使得 \(∠AEF=45°\)，若存在，请求出点 \(F\) 的坐标；若不存在，说明理由。

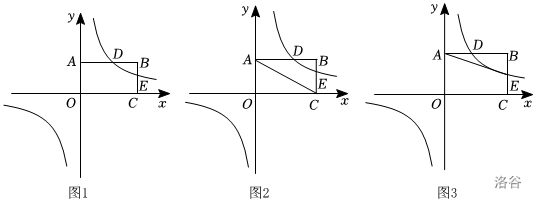
第一、二问很好做，直接求坐标相似即可，注意线段之间的关系包括位置关系和数量关系。

求得 \(y=\frac{12}{x},B(6,3),D(4,3),E(6,2)\)。

这里的策略是，构造等腰直角三角形，然后再用一线三垂直模型解答。

这里分类讨论。如图 \(1\) 和图 \(3\)。

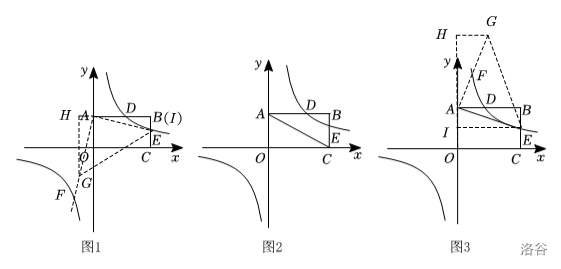
文中的图也许不标准。但是必有 \(l_{GE}\) 与反比例函数交于两点（\(F,E\)）。

所以我们可以求得 \(G_1(1,9),G_2(-1,-3)\)。所以可求得:

\[l_{EG_{1}}: y=-\frac{7}{5}x+\frac{52}{5} \tag{1} \]

\[l_{EG_{2}}: y=\frac{7}{5}x+\frac{16}{7} \tag{2} \]

将其分别与 \(y=\frac{12}{x}\) 联立，得到两个方程。

\[\frac{5}{7}x^2-\frac{52}{5}x+12=0 \tag{1} \]

\[\frac{5}{7}x^2-\frac{16}{7}x-12=0 \tag{2} \]

这里直接解实在太太太太太太费时间了，这里推荐使用韦达定理。因为我们已知有一根 \(x=6\)。

最后算出：

\[F_1 \left(\frac{10}{7},\frac{42}{5}\right),F_2 \left(-\frac{14}{5},-\frac{30}{7}\right) \]

5.（2024秋·凤城市期末）

如图，一次函数 \(y=-x+3\) 的图象与反比例函数 \(y=\frac{2}{x}\) 在第一象限的图象交于 \(A(1,2)\) 和 \(B(2,1)\) 两点，与 \(x\) 轴交于点 \(C\)。

• 若点 \(P\) 在 \(y\) 轴上，\(Q\) 在双曲线上，当以 \(A\)、\(B\)、\(P\)、\(Q\) 为顶点的四边形是平行四边形时，直接写出 \(Q\) 点的坐标。

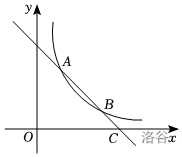
一二问删去了，对于第三问，我们可以直接将其抽象为数学模型。我们可知有三种情况。即分别以 \(AB,AP,AQ\) 为对角线的构造。那么怎么求解呢？

根据平行四边形的性质，对角线互相平分。那么根据中点坐标公式，定义中点 \(O\)，此时 \(AB\) 为对角线。有：

\[O\left(\frac{x_A+x_B}{2},\frac{y_A+y_B}{2}\right) , O\left(\frac{x_P+x_Q}{2},\frac{y_P+y_Q}{2}\right) \]

所以此时：

\[x_A+x_B=x_P+x_Q,y_A+y_B=y_P+y_Q \]

同理可算出三种情况：

\(Q(-1,-2),Q(1,2)(舍去)Q(3,\frac{2}{3})\)。

6.（2023秋·碑林区校级月考）

如图，一次函数 \(y=kx+b(k≠0)\) 的图象与反比例函数 \(y=\frac{m}{x}(x>0)\) 的图象交于 \(A(2,a)\)、\(B(8,-1)\) 两点。

• 求反比例函数与一次函数的关系式；

• 在 \(x\) 轴上是否存在一点 \(P\)，平面坐标系内是否存在一点 \(Q\)，使以 \(A\)、\(B\)、\(P\)、\(Q\) 为顶点的四边形为矩形?若存在，求出点 \(P\) 的坐标；若不存在，请说明理由。

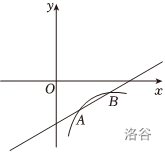
第一问直接求出 \(y=\frac{8}{x},l_{AB}:y=\frac{1}{2}x-5,A(2,-4)\)。

第二问我们想到，一个矩形，其实就是两个直角三角形拼成的。所以问题转化为是否有一点 \(P\)，使得 \(A,B,P\) 构成直角三角形？

两线一圆构造即可。

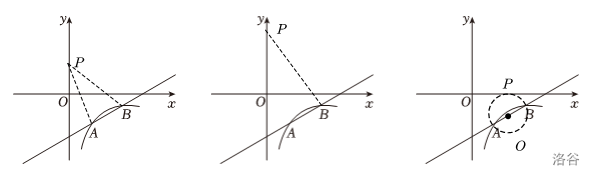
这里解释一下「一圆」。因为直径所对的圆周角是直角，所以直接取 \(AB\) 的中点为 \(O\)，以 \(O\) 为圆心，\(OA\) 为半径画圆。与 \(x\) 轴交点即为所求。即：

设 \(P(m,0)\)。

\[\sqrt{(m-5)^2+(\frac{5}{2})^2}=\frac{3\sqrt{5}}{2} \]

解得 \(m=5 \pm \sqrt{5}\)。

7.（2022秋·清原县期末）

如图，在平面直角坐标系中，\(\triangle AOB\) 的边 \(OB\) 在 \(y\) 轴上，边 \(AB\) 与 \(x\) 轴交于点 \(D\)，且 \(BD=AD\)，反比例函数 \(y=\frac{k}{x} \ (x>0)\) 的图象经过点 \(A\)，若 \(S_{\triangle AOB}=1\)，求 \(k\) 的值。

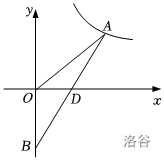
过 \(A\) 点作垂，倍长中线即可。

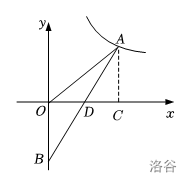
可得 \(\triangle DOB \cong \triangle DCA\)。

所以：

\[S_{\triangle AOB}=S_{\triangle AOD}+S_{\triangle DOB}=S_{\triangle AOD}+S_{\triangle DAC}=S_{\triangle AOC}=\frac{|k|}{2}=1 \]

所以 \(k=2\)。（负值舍去）

8.（2022·衡阳）

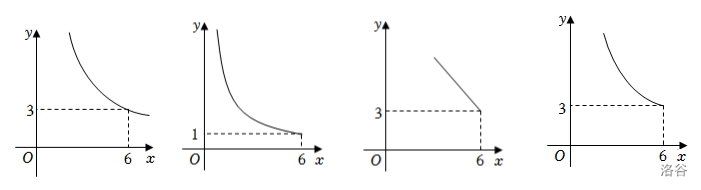
如图，在四边形 \(ABCD\) 中，$ \angle B=90°,AC=6,AB \parallel CD\(，\)AC$ 平分 \(\angle DAB\)。设 \(AB=x,AD=y\)，则 \(y\) 关于 \(x\) 的函数关系用图象大致可以表示为？

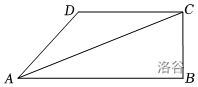
过 \(G\) 点作垂，相似即可。

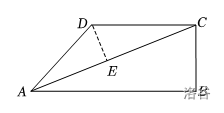
可得 \(\triangle ABC \sim \triangle AED\)。

所以：

\[\frac{AC}{AD}=\frac{AB}{AE} \]

即

\[\frac{6}{y}=\frac{3}{x},y=\frac{18}{x} \]

又因为 \(AC > AB\)，所以 \(AB <6\)，因此选第四个图。