【铅垂定理全集】水平宽和铅垂高

前言

• 水平宽铅垂高法是一种求在坐标系中求三角形的面积、求最值的方法。这种方法十分经典，在应试中大量使用，却很少有人对其系统总结。即使有相关文章，也缺少了许多证明过程。为此，本文介绍了水平宽铅垂高法在各个类型题目中的应用。

• 为了区分本文中的定义和正常数学公式，定义所有粗体 \(\boldsymbol{a}\) 和 \(\boldsymbol{h}\) 作为水平宽和铅垂高线段的符号。其余非粗体字母按照数学法则照常使用。本文中所有的内置定理在本文中引用时都加了粗体。粗体内容包括但不限于定理引用。

平面直角坐标系中的定理：

\[l_1 \parallel l_2 \Leftrightarrow k_{l_1}=k_{l_2} \]

\[l_1 \perp l_2 \Leftrightarrow k_{l_1}k_{l_2}=-1 \]

\[k_{l}=\frac{|y_1-y_2|}{|x_1-x_2|} \]

上下平移 \(a\) 个单位长度

\[l:y=kx+b \pm a \]

左右平移 \(a\) 个单位长度

\[l:y=k(x \pm a)+b \]

两点之间距离公式 \(A(x_1,y_1),B(x_2,y_2)\)

\[S=\sqrt{(x_1-x_2)^{2}+(y_1-y_2)^{2}} \]

中点坐标公式 \(A(x_1,y_1),B(x_2,y_2)\)

\[M(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}) \]

水平宽和铅垂高

1. 水平宽和铅垂高中的定义与定理

如图 \(1\)，这是一个锐角三角形。考虑求它的面积。

我们可以将其放进一个坐标系中进行观察。如图 \(2\)。

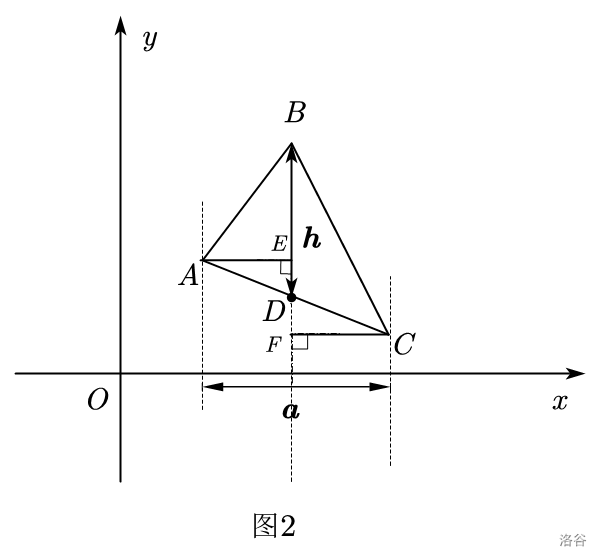
定义 1.1 三角形的水平宽

• 三角形任意两个顶点的投影长度。记作 \(\boldsymbol{a}\)。

定义 1.2 三角形的铅垂高

• 过三角形第三点作水平宽的垂线，交对边所在的直线为一点。这两点的距离叫做铅垂高。记作 \(\boldsymbol{h}\)。

定义 5.1 四边形的水平宽

• 四边形的任意一条对角线上的两个顶点的投影长度。记作 \(\boldsymbol{a}\)。

定义 5.2 四边形的铅垂高

• 分别过四边形另外两个顶作水平宽的垂线，分别交该对角线所在的直线为一点。这两组点的距离分别记作 \(\boldsymbol{h_1,h_2}\)。这两组点的距离之和是该四边形的铅垂高，记作 \(\boldsymbol{h_1+h_2}\)。

定理 1.1

• 因为同一平面内过直线外一点有且只有一条直线与已知直线垂直，所以当确定了一条水平宽后，铅垂高有且只有一条。

定理 1.2

• 三角形的一组铅垂高与水平宽相互垂直。即 \(\boldsymbol{a} \perp \boldsymbol{h}\)。

定理 1.3

• 三角形的面积等于其一组水平宽与铅垂高之积的一半。即 \(S_{\triangle ABC}=\frac{1}{2}\boldsymbol{a} \boldsymbol{h}\)。

• 证明（图 \(2\)）：
  过点 \(A,C\) 分别作 \(AE,CF \perp BD\)，垂足为 \(E,F\)。

  根据定理 1.2可得 \(AE+CF=\boldsymbol{a}\)，已知 \(BD=\boldsymbol{h}\)。

  所以

  \[\begin{align*} S_{\triangle ABC} &= S_{\triangle ABD}+S_{\triangle BCD}\\ &= \frac{1}{2} AE \cdot BD + \frac{1}{2} CF \cdot BD \\ &= \frac{1}{2} BD \cdot (AE+CF) \\ &= \frac{1}{2} \boldsymbol{a} \boldsymbol{h} \end{align*} \]

定理 1.4

• 一个三角形有三对水平宽和铅垂高。如图 \(3\)。任意一组水平宽和铅垂高都满足 \(S_{\triangle ABC}=\frac{1}{2}\boldsymbol{a} \boldsymbol{h}\)。

  

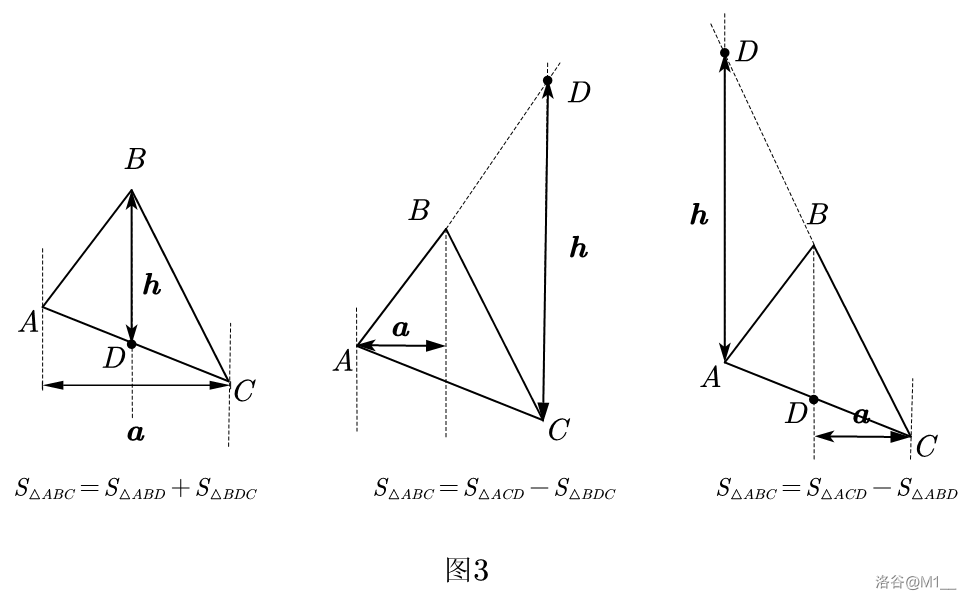
定理 5.1：

• 四边形的任意一组水平宽和铅垂高都满足：

\[S_{四边形 ABCD}=\frac{1}{2} \boldsymbol{a \cdot (h_1+h_2)} \]

详细证明过程见下文【番外篇】。

2. 一般三角形中的水平宽和铅垂高

2.1 锐角三角形

如图 3，一个锐角三角形三角形有三对水平宽和铅垂高。它们都满足上述定理。可以用割补法进行证明。

2.2 钝角三角形

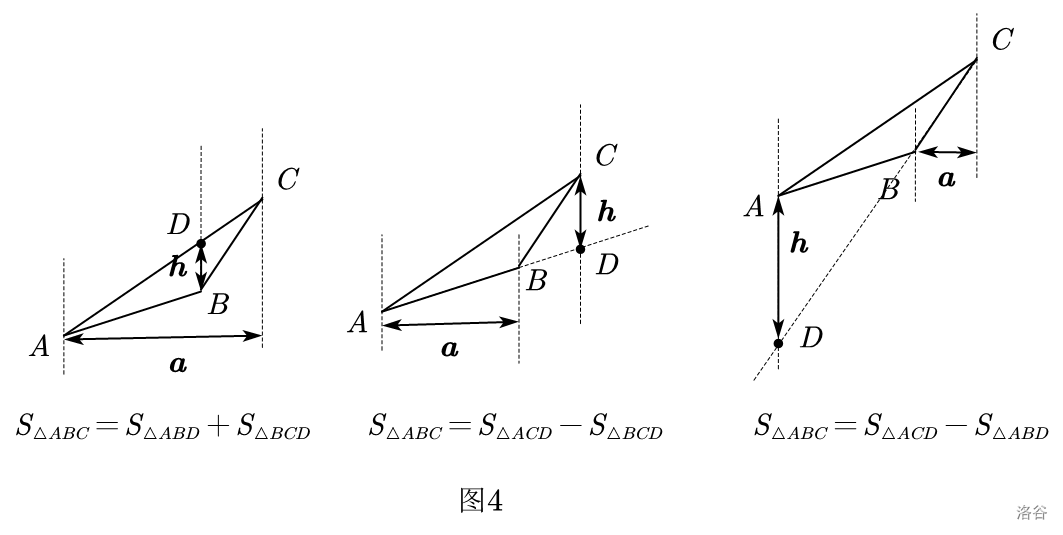
相应地，钝角三角形同样满足上述定理。

可以用割补法进行证明。如图 \(4\)。

综上可得，对于任意一个三角形，我们都可以利用水平宽铅垂高来求出其面积。

3. 水平宽铅垂高与一次函数

• 水平宽和铅垂高被广泛地应用于一次函数中的求三角形面积问题。

• 这一类题的大致思路是：先找到水平宽与铅垂高（一般有一个为定值）；再求水平宽与铅垂高的长度，最后计算面积。

• 对于一些非平面直角坐标系中的题目，我们可以考虑暴力建系因为初中几何以直线居多，所以将这类题目放入一次函数类目中。找到一个直角，以直角顶点为坐标原点，构建平面直角坐标系。然后求得解析式联立即可。

• 对于最值问题，一次函数部分涉及较少，二次函数部分涉及较多，这里不再赘述。

例 1（2023秋·桐城市校级期末）

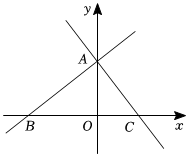
如图，在平面直角坐标系中，直线 \(y=kx+b\) 与 \(x\) 轴交于点 \(B(-5,0)\)，与 \(y\) 轴交于点 \(A\)，直线 \(y=-\frac{4}{3}x+4\) 过点 \(A\),与 \(x\) 轴交于点 \(C\)，点 \(P\) 是 \(x\) 轴上方一个动点。

• 求直线 \(AB\) 的函数表达式；
• 若点 \(P\) 在射线 \(BA\) 上，且 \(S_{\triangle APC}=S_{\triangle AOB}\)，求点 \(P\) 的坐标。

跳过第一问得 \(l_{AB}:y=\frac{4}{5}x+4, \ A(0,4), \ B(-5,0), \ C(3,0), \ S_{\triangle AOB}=10\)。

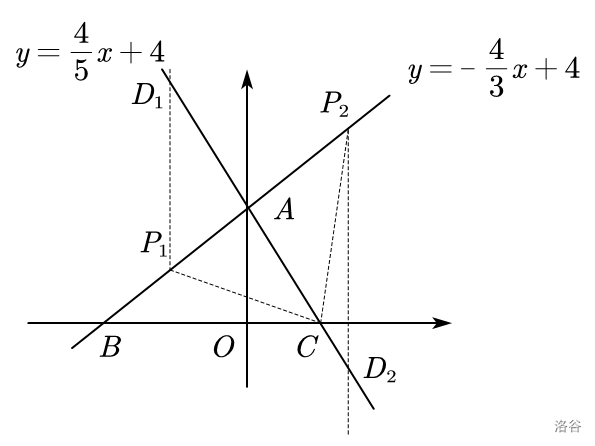
第二问我们就可以用水平宽铅垂高公式。以 \(OC\) 为水平宽，\(DP\) 为铅垂高。则 \(S_{\triangle AOB}=\frac{1}{2}OC \cdot DP=10\)。

此时设 \(D(m,\frac{4}{5}m+4),P(m,-\frac{4}{3}m+4)\)，则 \(|y_{D}-y_{P}|=DP\)。

所以 \(\frac{1}{2} |y_{D}-y_{P}| \times 3=10\)，解得 \(m=-\frac{25}{8}\) 或 \(m=\frac{25}{8}\)。
所以 \(P(-\frac{25}{8},\frac{3}{2})\) 或 \(P(\frac{25}{8},\frac{13}{2})\)。

如果没有平面直角坐标系，建议直接暴力建系，找到一个直角顶点，以这一顶点为原点作平面直角坐标系即可。

例 2（2010 春·南浔区期末）

如图，已知边长为 \(a\) 的正方形 \(ABCD\)，\(E\) 为 \(AD\) 中点，\(P\) 为 \(CE\) 中点，求三角形 \(BPD\) 的面积。

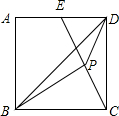
以点 \(B\) 为原点 \(O\)，构建平面直角坐标系，如图：

因为四边形 \(ABCD\) 是正方形，所以对角线的解析式为：\(l_{BD}:y=x\)。

由题意得 \(E(\frac{a}{2} , a) \ ,C(a,0)\)。

由中点坐标公式可得 \(P(\frac{x_E+x_C}{2},\frac{y_E+y_C}{2})\)，即 \(E(\frac{3}{4}a,\frac{1}{2}a)\)，即 \(l_{BP}:y=\frac{2}{3}x\)。

此时 \(BC\) 为水平宽，\(PQ\) 为铅垂高。可得：\(l_{PQ}:x=\frac{3}{4}a\)，联立 \(l_{BD},l_{PQ}\)，得：

\( \left\{\begin{matrix} l_{BD}:y=x\\ l_{PQ}:x=\frac{3}{4}a \end{matrix}\right. \) 解得 \( \left\{\begin{matrix} x=\frac{3}{4}a\\ y=\frac{3}{4}a \end{matrix}\right. \)，所以 \(Q(\frac{3}{4}a,\frac{3}{4}a)\)。

所以 \(PQ=|y_Q-y_P|=|\frac{3}{4}a-\frac{1}{2}a|=\frac{1}{4}a\)。

所以 \(S_{\triangle BDP}=\frac{1}{2}PQ \cdot BC=\frac{1}{2} \times \frac{1}{4} a^{2}=\frac{1}{8} a^{2}\)

例 3（2022 秋·成都期中）

北辛数学竞赛 T6。

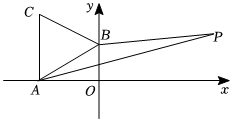
如图所示，\(A(-\sqrt{3},0),B(0,1)\) 分别为 \(x\) 轴、\(y\) 轴上的点，\(△ABC\) 为等边三角形，点 \(P(3,a)\) 在第一象限内，且 \(\triangle{ABP}\) 的面积 \(S_{\triangle{ABP}}\) 与 \(\triangle{ABC}\) 的面积 \(S_{\triangle{ABC}}\) 满足 \(2S_{\triangle{ABP}}=S_{\triangle{ABC}}\)，求 \(a\) 的值。

考虑水平宽铅垂高，如图。

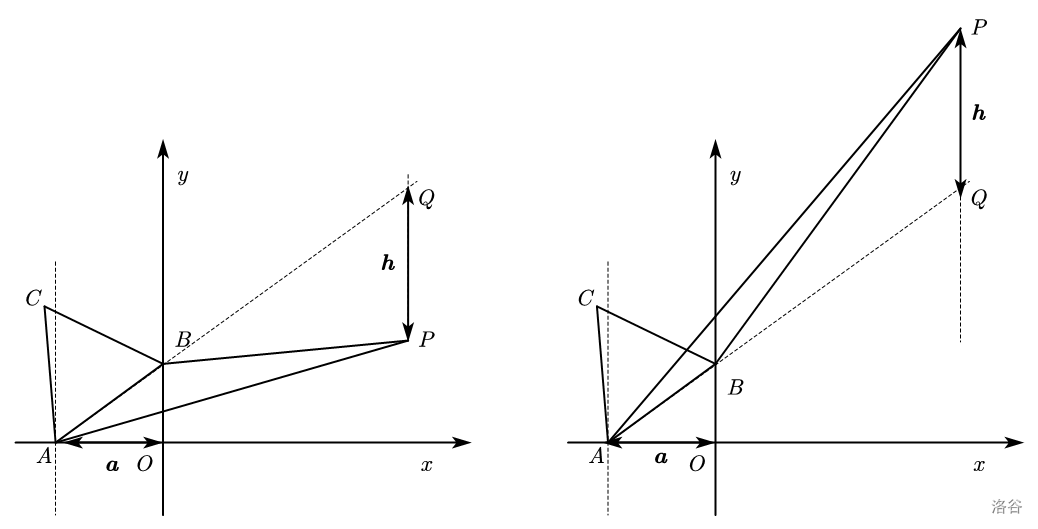
根据点的坐标可以看出，\(AO=\sqrt{3},OB=2\)。

所以 \(AB=\sqrt{AO^2+BO^2}=\sqrt{({\sqrt{3}})^{2}+1^2}=2\)。

我们知道，对于一个等边三角形，另 \(a\) 为其边长，面积为：

\[S=\frac{\sqrt{3}}{4} {a}^{2} \]

所以 \(S_{\triangle ABC} = \frac{\sqrt{3}}{4} AB^2=\frac{\sqrt{3}}{4} \times 2^2 = \sqrt{3}\)。

这时作水平宽铅垂高，得 \(OA=\boldsymbol{a},PQ=\boldsymbol{h}\)。

求得 \(l_{AB}:y=\frac{\sqrt{3}}{3}x+1\)。

因为 \(P(3,a)\)，所以 \(Q(3,\sqrt{3}+1)\)。

所以 \(PQ=|y_P-y_Q|=|(\sqrt{3}+1)-a|\)。因为 \(OA=\sqrt{3}\)，所以可列方程：

\[2 \cdot \frac{\sqrt{3}|(\sqrt{3}+1)-a|}{2}=\sqrt{3} \]

解得 \(a=\sqrt{3}\) 或 \(a=2+\sqrt{3}\)。

例 4（2021 春·青山区期末）

已知，在平面直角坐标系中，三角形 \(ABC\) 三个顶点的坐标分别为 \(A(a,0),B(b,4),C(2,c)\)，\(BC \parallel x\) 轴，且 \(a,b\) 满足 \(\sqrt{a+b-1}+|2a-b+10|=0\)。

• 求 \(a,b,c\) 的值。

• 如图 \(1\)，在 \(y\) 轴上是否存在点 \(D\)，使三角形 \(ABD\) 的面积等于三角形 \(ABC\) 的面积？若存在，请求出点 \(D\) 的坐标；若不存在，请说明理由。

• 如图 \(2\)，连接 \(OC\) 交 \(AB\) 于点 \(M\)，点 \(N(n,0)\) 在 \(x\) 轴上，若三角形 \(BCM\) 的面积小于三角形 \(BMN\) 的面积，直接写出 \(n\) 的取值范围。

  

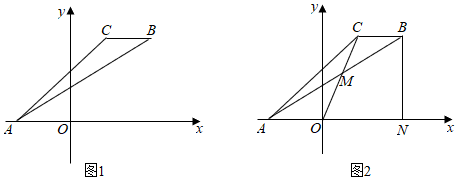
这是一道很典型的水平宽铅垂高题。

第一题跳过，得 \(a=-3,b=4,c=4\)。

接下来看第二问。已知 \(A(-3,0) ,\ B(4,4), \ C(2,4)\)。显然 \(D\) 点有两种情况，如果硬用割补法较为繁琐。如果使用水平宽铅垂高比较简单。

显然可以求出 \(S_{\triangle ABC}=4\)。具体求法也可以用水平宽和铅垂高。如下：

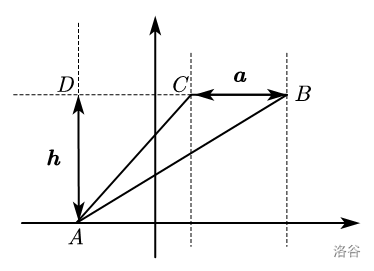
所以 \(S_{\triangle ABC}=\frac{1}{2} BC \cdot AD=\frac{1}{2} |x_B-x_C| \cdot |y_C|=\frac{1}{2} \times 2 \times 4=4\)。

接下来求 \(S_{\triangle ABD}\)。设 \(D(0,m)\)。

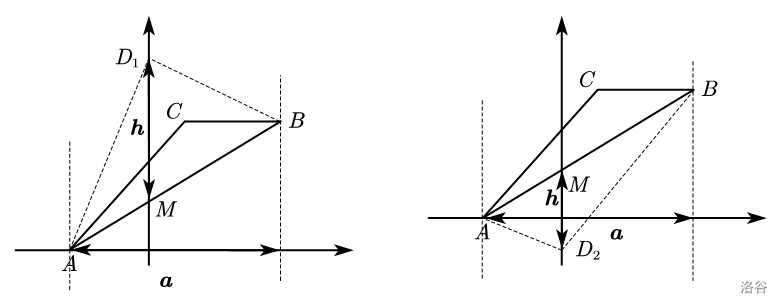
所以 \(S_{\triangle ABD}=\frac{1}{2} \boldsymbol{ah}=\frac{1}{2}|x_A-x_B| \cdot |m-y_M|\)。

已知 \(A,B\) 两点坐标，不难求出 \(l_{AB}:y=\frac{4}{7}x + \frac{12}{7}\)。所以 \(M(0,\frac{12}{7}), \ y_m=\frac{12}{7}\)。这里设 \(AB\) 与 \(y\) 轴交点为 \(M\)。

所以可得方程：

\[|m-\frac{12}{7}| \cdot 7 \times \frac{1}{2}=4 \]

解得 \(m=\frac{20}{7}\) 或 \(m=\frac{4}{7}\)。

所以 \(D(0 , \frac{20}{7})\) 或 \(D(0 , \frac{4}{7})\)。

第三问同样，用水平宽铅垂高公式会简易许多。

首先求得 \(S_{\triangle BCM}\)，如下图：

已知 \(A(-3,0) ,\ B(4,4), \ C(2,4)\)。

不难求出 \(l_{OC}:y=2x\)。联立 \(l_{OC}\) 和 \(l_{AB}\) 得：

\( \left\{\begin{matrix} l_{OC}:y=2x\\ l_{AB}:y=\frac{4}{7}x + \frac{12}{7} \end{matrix}\right. \) 解得 \( \left\{\begin{matrix} x=\frac{6}{5}\\ y=\frac{12}{5} \end{matrix}\right. \)，所以 \(M(\frac{6}{5},\frac{12}{5})\)

所以

\[S_{\triangle BCM}=\frac{1}{2} BC \cdot MD=\frac{1}{2} |x_B-x_C| \cdot |y_C-y_M|=\frac{1}{2} |4-2| \cdot |4-\frac{12}{5}|=\frac{1}{2} \times 2 \times \frac{8}{5}=\frac{8}{5} \]

接下来就要分类讨论 \(N\) 点的位置。分两种情况，如图：

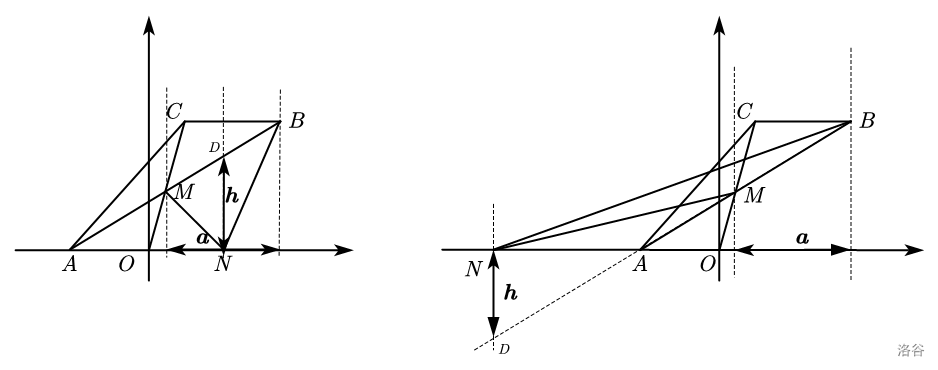
因为设 \(N(n,0)\)，\(DN\) 位于同一条直线上，所以 \(D(n,\frac{4}{7}n+\frac{12}{7})\)。

所以，

\[S_{\triangle BMN}=\frac{1}{2} \boldsymbol{ah}=\frac{1}{2} \cdot |x_M-x_B| \cdot |y_D-y_N|=\frac{1}{2} \times |4-\frac{6}{5}| \cdot |\frac{4}{7}n+\frac{12}{7}-0| =\frac{1}{2} \times \frac{14}{5} \cdot |\frac{4}{7}n+\frac{12}{7}| \]

所以可列方程：

\[\frac{1}{2} \times \frac{14}{5} \cdot |\frac{4}{7}n+\frac{12}{7}|>\frac{8}{5} \]

解得：\(n>-1\) 或 \(n<-5\)。

例 5（笔者原创）

阅读以下材料，回答问题：

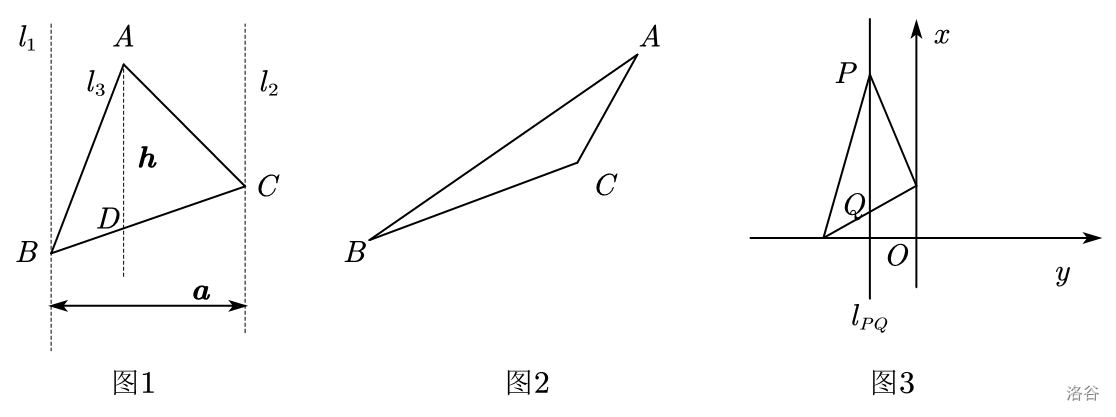
为了进一步探究三角形面积的求法，某数学兴趣小组做了如下尝试，如图 \(1\)，在锐角三角形 \(ABC\) 中，过点 \(A,B,C\) 分别作直线 \(l_1 \parallel l_2 \parallel l_3，l_3\) 交 BC 于点 D。令 \(AD=\boldsymbol{h}\)，\(l_1,l_2\) 间的距离为 \(\boldsymbol{a}\)，则 \(S=\frac{1}{2} \boldsymbol{ah}\)。

• 当 \(\triangle{ABC}\) 为钝角三角形时，如图 \(2\)，请仿照材料画出图像，指出 \(S\) 与 \(\boldsymbol{ah}\) 的数量关系并加以证明。

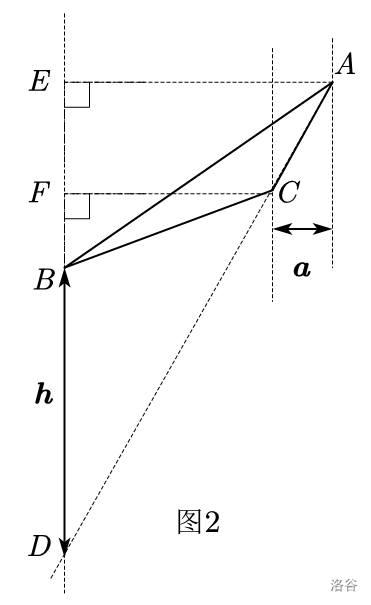
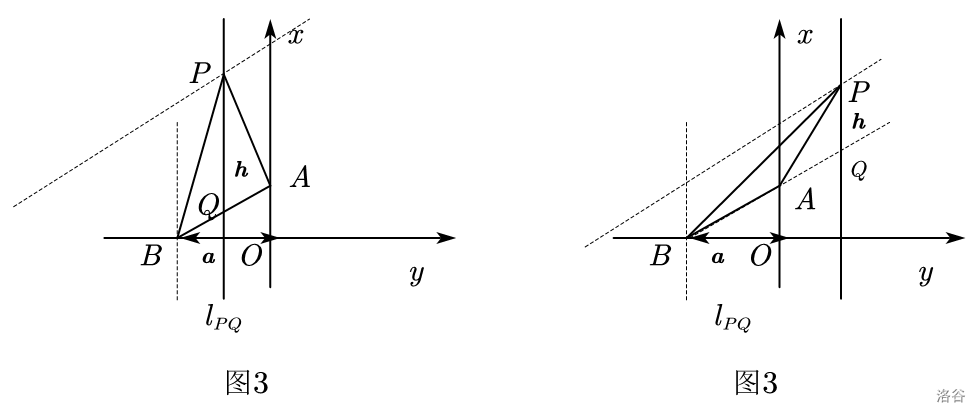
• 如图 \(3\)，在平面直角坐标系中，\(A(0,3),B(-3,0),l_{AB}:y=kx+b\)，动直线 \(l_{pq}:x=t\) 沿 \(x\) 轴运动交 \(AB\) 所在的直线于点 \(Q\)。点 \(P(t,3t+9)\) 在直线 \(AB\) 上方且在 \(l_{PQ}\) 上.

  • 求 \(l_{AB}:y=kx+b\) 的函数表达式.
  • 设 \(\triangle{ABC}\) 的面积为 \(S\)，当 \(t > -3\) 时，\(S\) 的值是否随 \(t\) 值的变化而变化？若变化，试求出 \(S\) 与 \(t\) 的函数关系式；若不变，请求出 \(S\) 的值。
  • 保持上述条件不变，若 \(S\) 的值为定值，请直接写出 \(P(t,kt+9)\) 中 \(k\) 的值.

对于第一问，如图：

如图，分别过点 \(A,B,C\) 作 \(l_{1} \parallel l_{2} \parallel l_{3}\)，\(l_{3}\) 交 \(AC\) 的延长线为点 \(D\)。分别过点 \(A,C\) 作 \(AE,CF \perp BD\)，垂足为 \(E,F\)。

则 \(AE-CF=\boldsymbol{a},BD=\boldsymbol{h}\)。

所以

\[ \begin{align*} S_{\triangle ABC} &= S_{\triangle ABD}-S_{\triangle BCD}\\ &= \frac{1}{2} AE \cdot BD - \frac{1}{2} CF \cdot BD \\ &= \frac{1}{2} BD \cdot (AE-CF) \\ &= \frac{1}{2} \boldsymbol{a} \boldsymbol{h} \end{align*} \]

对于第二问，可求得 \(l_{AB}:y=x+3\)，所以 \(Q(t,t+3)\)。

作水平宽铅垂高。因为 \(P(t,3t+9)\)，则 \(\boldsymbol{h}=|y_P-y_Q|=3t+9-(t+3)=2t+6,\boldsymbol{a}=|x_A-x_B|=3\)。

所以

\[S=\frac{1}{2} \boldsymbol{ah}=\frac{3(2t+6)}{2}=3t+9 \]

对于第三问，考虑代数证明：

此时因为 \(P(t,kt+9)\)，所以 \(l_{PQ}\) 与 \(l_{AB}\) 的交点 \(Q\) 恒为 \((t,t+3)\)。

所以此时

\[S=\boldsymbol{ah}=\frac{1}{2}|x_A-x_B| \cdot |y_P-y_Q|=\frac{3}{2}[kt+9-(t+3)]=\frac{3t(k-1)+6}{2} \]

做到这一步我们显然就可以看出，这道题就是要求出 \(S\) 的值与 \(t\) 无关时 \(k\) 的值。

令 \(k-1=0,k=1\)。

所以当 \(k=1\) 时，\(S\) 的值为定值。

考虑几何证明。

我们知道定理

\[l_1 \parallel l_2 \Leftrightarrow k_{l_1}=k_{l_2} \]

• 所以，当 \(l_{PQ} \parallel l_{AB}\) 时，铅垂高不变。可以抽象成这个模型：

  

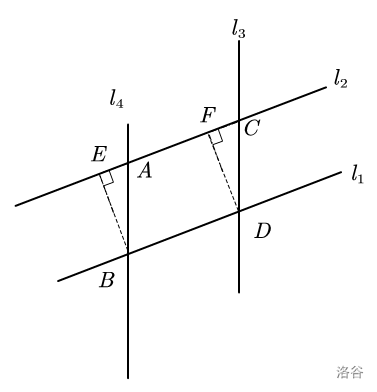
  已知 平面内有 \(l_1 \parallel l_2\)，有 \(l_{3}\) 分别交 \(l_1,l_2\) 于 \(D,C\)，有 \(l_3\) 分别交 \(l_1,l_2\) 于 \(B,E\)。且 \(l_3 \parallel l_4\)。

  求证 \(AB=CD\)

  证明： 分别过点 \(B,D\) 作 \(BE,CF\)，垂足为 \(E,F\)。

  所以 \(\angle AEB=\angle CFD=90°\)。

  又因为 \(l_3 \parallel l_4\)，所以 \(\angle EAB=\angle FCD\)（两直线平行，同位角相等）。

  又因为 \(l_1 \parallel l_2\)，所以 \(BE=DF\)（平行线间的距离处处相等）。

  所以 \(\triangle AEB \cong \triangle CFD \ (AAS)\)。

  所以 \(AB=CD\)。

现在将这个模型放进题目中可得：当 \(l_{PQ} \parallel l_{AB}\) 时，铅垂高不变。

又因为水平宽始终为定值，所以 \(S\) 为定值。

证毕。所以 \(k=k_{AB}=1\)。附图：

4. 水平宽铅垂高和反比例函数

• 水平宽铅垂高在反比例函数中的应用主要是求三角形面积。一般不用其求三角形最值。

• 因为近年来中考对反比例函数的考察程度不高，因此这里只放几个例题。

例 1（2019春·北碚区期末）

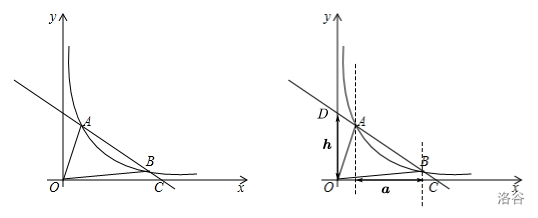
如图，一次函数 \(y_1=-\frac{2}{3}x+b\) 的图象与反比例函数 \(y_2=\frac{k}{x}(x>0)\) 的图象交于 \(A\)、\(B\) 两点，与 \(x\) 轴交于点 \(C\)，且点 \(A\) 的坐标为 \((1,2)\)，点 \(B\) 的横坐标为 \(3\)。

• 在第一象限内，当 \(x\) 取何值时，\(y_1 > y_2\)？（根据图直接写出结果）

• 求反比例函数的解析式及 \(\triangle AOB\) 的面积。

第一问求出 \(A(1,2),B(3,\frac{2}{3})\)，双曲线解析式为 \(y_2=\frac{2}{x}\)，\(l_{AB}:y_1=\frac{2}{3}x+\frac{8}{3}\)。

第二问考虑水平宽铅垂高，\(\boldsymbol{a}=|x_B-x_A|=2\)。可求得 \(D(0,\frac{8}{3})\)。

\(\boldsymbol{h}=OD=\frac{8}{3}\)，所以 \(S_{\triangle AOB} = \frac{1}{2} \boldsymbol{ah}=\frac{8}{3}\)。

例 2（2015秋·雁塔区校级月考）

如图，反比例函数 \(y=-\frac{8}{x}\) 一与一次函数 \(y=-x+2\) 的图象交于 \(A\)、\(B\) 两点。

• 求 \(A\)、\(B\) 两点的坐标；
• 观察图象，直接写出 \(x\) 为何值时，一次函数值大于反比例函数？
• 求 \(\triangle AOB\) 的面积。

第一题直接联立解析式，得：

\( \begin{cases} y=-\frac{8}{x} \\ y=-x+2 \end{cases} \) 得 \(A(-2,4),B(4,-2)\)。

第二理由观察可得：\(x < -2\) 或 \(0 < x < 4\)。

第三题考虑水平宽铅垂高，可得 \(D(0,2)\)，所以 \(\boldsymbol{h}=OD=2\)。

又因为 \(\boldsymbol{a}=|x_B-x_A|=6\)，所以：

\[S_{\triangle AOB}=\frac{1}{2} \boldsymbol{ah}=\frac{1}{2} \times 2 \times 6=6 \]

例 3（2024春·巧家县校级月考）

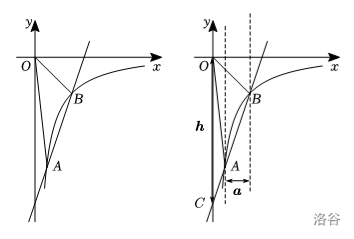
如图,在平面直角坐标系 \(xOy\) 中，一次函数 \(y_1=3x-12\) 与反比例函数 \(y_2=\frac{k}{x}(k \neq 0,x > 0)\) 的图象交于 \(A,B\) 两点，已知点 \(A\) 的横坐标为 \(1\)。

• 求 \(k\) 的值。
• 连接 \(OA,OB\)，求 \(\triangle AOB\) 的面积。

对于第一题，求得 \(A(1,-9)\)，代入反比例函数中可得 \(k=-9\)，所以反比例函数关系式为 \(y=-\frac{9}{x}\)。

对于第二题，考虑水平宽铅垂高。直接联立方程组得：

\( \begin{cases} y=-\frac{9}{x} \\ y=3x-12 \end{cases} \) 得 \(B(3,-3)\)。

所以 \(\boldsymbol{a}=|y_B-y_A|=3-1=2\)，\(D(0,-12)\)。

所以：

\[\boldsymbol{h}=OD=12 \]

所以：

\[S_{\triangle AOB} = \frac{1}{2} \boldsymbol{ah}=\frac{1}{2} \times 2 \times 12=12 \]

5. 水平宽铅垂高和二次函数

• 与一次函数相对应，水平宽铅垂高在二次函数中主要被应用于求三角形面积最值和面积数量关系。

• 因为我们知道，二次函数图像和一次函数图像差别较大，二次函数图像的对称轴对应的纵坐标即为函数的最大值。

• 所以，水平宽铅垂高在二次函数中的应用便应运而生。但求的时候要记住，符合条件的点是有多个的。

• 当然，还有一些较好的方法例如平行线转移法，这些方法在某种意义上来说比铅垂线法更加直观，在后文或许会提到。

二次函数前置知识

	解析式	顶点坐标
一般式	\(y=ax^2+bx+c\)	\((-\frac{b}{2a},\frac{4ac-b^2}{4a})\)
顶点式	\(y=a(x-h)^2+k\)	\((h,k)\)
交点式	\(y=a(x-x_1)(x-x_2)\)	\((-\frac{b}{2a},\frac{4ac-b^2}{4a})\)

对于二次函数一般式 \(y=ax^2+bx+c\)：

• 当 \(a > 0\) 时，函数有最小值。
• 当 \(a < 0\) 时，函数有最大值。

我们就可以利用这个性质求三角形面积最值。

例 1（2023·南通二模）【配方法求最值】

如图，二次函数 \(y=-x^{2}-2x+3\) 与 \(y\) 轴交于点 \(A(0,3)\)，与 \(x\) 轴交于点 \(B(-3,0)\)，\(P\) 为抛物线上一点且点 \(P\) 在线段 \(AB\) 上方，求 $S_{\triangle ABP} $ 的最大值。

同样是作水平宽铅垂高。如图。

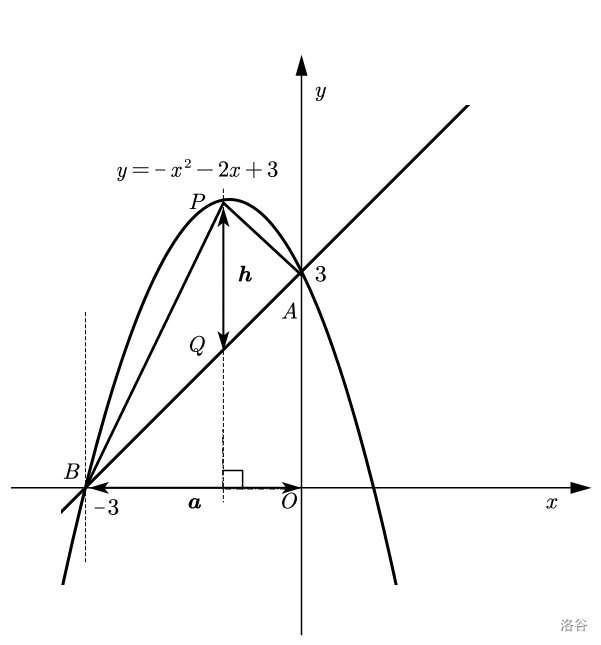
由图可得，\(OB=\boldsymbol{a},PQ=\boldsymbol{h}\)。因为 \(OB\) 的长为定值，所以问题转化为求 \(PQ\) 的最大值。

可求得 \(l_{AB}:y=x+3\)。

设 \(P(m,-m^2-2m+3)\)，则 \(Q(m,m+3)\)。

所以：

\[PQ=|y_P-y_Q|=-m^2-2m+3-(m+3)=-m^2-3m \]

配方，得：

\[-m^2-3m=-(m^2+3m+\frac{9}{4}-\frac{9}{4})=-(m+\frac{3}{2})^2+\frac{9}{4} \]

因为 \((m+\frac{9}{4})^2 \ge 0\)，所以 \(-(m+\frac{9}{4})^2 \le 0\)，所以 \([-(m+\frac{9}{4})^2 ]_{\max} = 0\)，所以 \(\boldsymbol{h}_{\max}=PQ_{\max}=\frac{9}{4}\)。

所以

\[S_{\triangle ABP}=\frac{1}{2} \boldsymbol{h_{\max}a}=\frac{1}{2} \times \frac{9}{4} \times 3=\frac{27}{8} \]

例 2（2024·沅江市一模）【公式法求最值】

如图，已知抛物线 \(y=ax²+bx+3\) 与 \(x\) 轴交于 \(A(-1,0)\)、\(B(3,0)\) 两点，与 \(y\) 轴交于点 \(C\)，连接 \(BC\)。

• 求抛物线的解析式；

• 若点 \(P\) 为线段 \(BC\) 上的一动点（不与 \(B\)、\(C\) 重合），$PM \parallel y $ 轴,且 \(PM\) 交抛物线于点 \(M\)，交 \(x\) 轴于点 \(N\)，当 \(\triangle BCM\) 的面积最大时，求点 \(P\) 的坐标。

第一问我们直接使用交点式 \(y=a(x-x_1)(x-x_2)\)，再代入 \(C(0,3)\) 即可求出抛物线解析式 \(y=-x^2+2x+3\)。

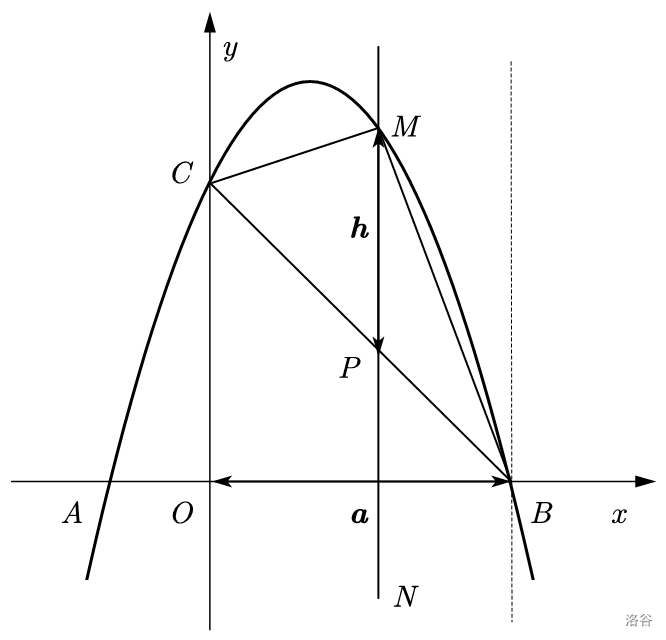
如图，考虑水平宽铅垂高。

因为 \(C(0,3),B(3,0)\)，所以 \(l_{BC}:y=-x+3\)。

这时设 \(P(m,-m+3)\)，则 \(M(m,-m^2+2m+3)\)。

所以：

\[\boldsymbol{h}=PM=|y_M-y_P|=-m^2+2m+3+m-3=-m^2+3m \]

显然 \(\boldsymbol{h}\) 有最大值，即：

\[\boldsymbol{h}_{\max}=\frac{4ac-b^2}{4a}=\frac{9}{4} \]

又因为 \(OB=\boldsymbol{a}\)，所以当 \(S_{\triangle BCM}\) 最大时，\(x_P=-\frac{b}{2a}=\frac{3}{2}\)。将其代入 \(l_{BC}:y=-x+3\) 中，可得 \(P(\frac{3}{2},\frac{3}{2})\)。

例 3（2024·达州中考）【面积关系问题】

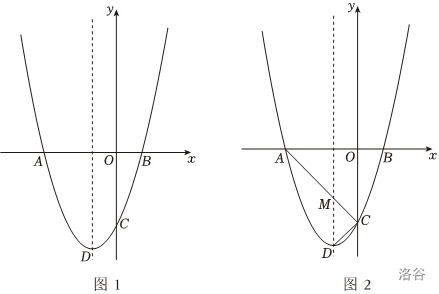
如图 \(1\)，抛物线 \(y=ax²+bx-3\) 与 \(x\) 轴交于点 \(A(-3,0)\) 和点 \(B(1,0)\)，与 \(y\) 轴交于点 \(C\)，点 \(D\) 是抛物线的顶点.

• 求抛物线的解析式；

• 如图 \(2\)，连接 \(AC,DC\)，直线 \(AC\) 交抛物线的对称轴于点 \(M\)，若点 \(P\) 是直线 \(AC\) 上方抛物线上一点，且 \(S_{\triangle PMC}=2S_{\triangle DMC}\)，求点 \(P\) 的坐标；

• 若点 \(N\) 是抛物线对称轴上位于点 \(D\) 上方的一动点，是否存在以点 \(N,A,C\) 为顶点的三角形是等腰三角形，若存在，请直接写出满足条件的点 \(N\) 的坐标；若不存在，请说明理由。

第一问和例 \(1\) 比较相似，通过相同思路求得解析式 \(C_{1}:y=x^2+2x-3\)。

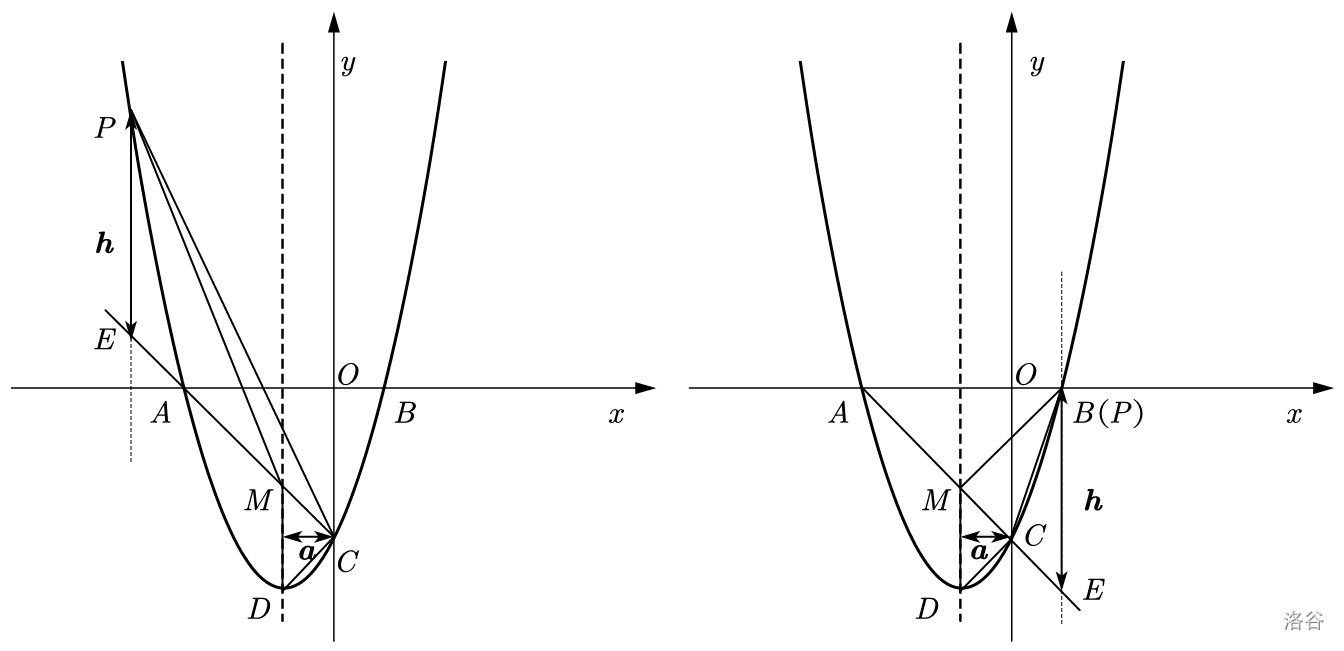
考虑第二问。因为题目要求 \(P\) 在 \(AC\) 上方，所以我们不用考虑绝对值的问题。

考虑求 \(AC\) 的函数表达式。已知 \(A(-3,0),C(0,-3)\)。所以 \(l_{AC}:y=-x-3\)。

这时设 \(E(m,-m-3),P(m,m^2+2m-3)\)。所以 \(\boldsymbol{h}=PE=m^2+2m-3+m+3=m^2+3m\)。

由题目可得 \(M,D\) 都在对称轴上，所以 \(x_M=-\frac{b_{C_{1}}}{2a_{C_{1}}}=-1\)。所以 \(M(-1,-2)\)。

所以 \(\boldsymbol{a}=|x_M-x_C|=1\)。\(2S_{\triangle CMD}=\frac{1}{2} \times 2 \boldsymbol{a} \cdot DM =2\)。

因此可列方程：

\[\frac{1}{2} \times 1 \cdot m^2+3m=2 \]

解得 \(m_1=1,m_2=-4\)。

所以 \(P1(1,0),P_2(-4,5)\)。

对于第三位，采取传统的两圆一线做法即可。这里不再赘述，附图：

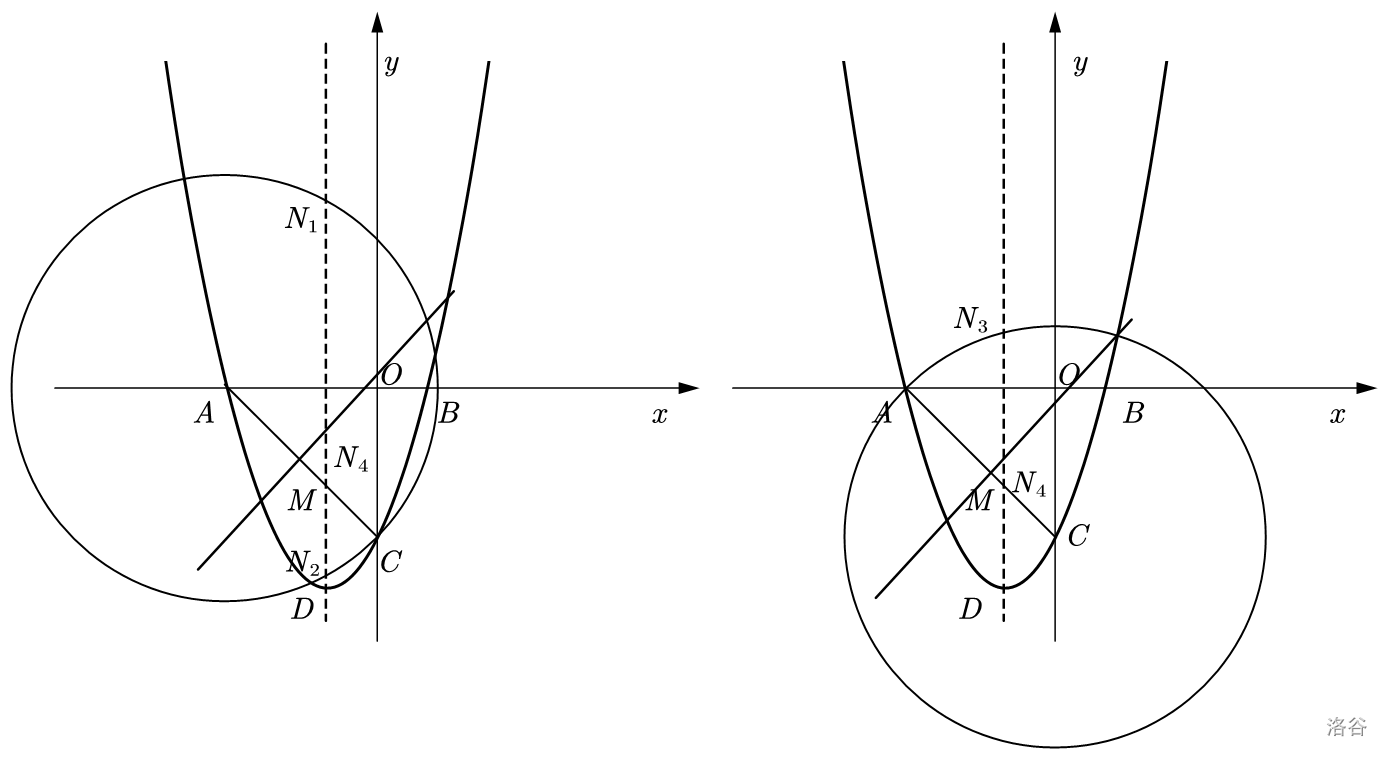
题外话：这道题的正解是平行线转移法。它的优势是不用算三角形的面积，只需要将 $l_{AC} $ 向上平移构造出一个新的一次函数，然后求其与一次函数的交点即可。并且，这种方法可以直观地表示出符合条件的点的位置。

例 4（2016·苏州）【等积思想】

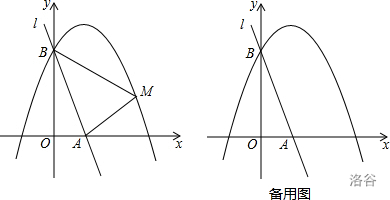
如图，直线 \(l:y=-3x+3\) 与 \(x\) 轴、\(y\) 轴分别相交于 \(A\)、\(B\) 两点，抛物线 \(y=ax^2-2ax+a+4(a<0)\) 经过点 \(B\)。

• 求该抛物线的函数表达式；

• 已知点 \(M\) 是抛物线上的一个动点，并且点 \(M\) 在第一象限内，连接 \(AM\)、\(BM\)，设点 \(M\) 的横坐标为 \(m\)，\(\triangle ABM\) 的面积为 \(S\)，求 \(S\) 与 \(m\) 的函数表达式，并求出 \(S\) 的最大值；

• 在上一问的条件下，当 \(S\) 取得最大值时，动点 \(M\) 相应的位置记为点 \(M'\)。

  • 写出点 \(M'\) 的坐标；
  • 将直线 \(l\) 绕点 \(A\) 按顺时针方向旋转得到直线 \(l'\)，当直线 \(l'\) 与直线 \(AM'\) 重合时停止旋转，在旋转过程中，直线 \(l'\) 与线段 \(BM'\) 交于点 \(C\)，设点 \(B\)、\(M'\) 到直线 \(l'\) 的距离分别为 \(d_1\)、\(d_2\)，当 \(d_1+d_2\) 最大时，求直线 \(l'\) 旋转的角度（即 \(\angle BAC\) 的的度数）。

首先看第一问。直接求出 \(B(0,3)\)，代入即可。得：\(C_1:y=-x^2+2x+3\)。

接下来看第二问，考虑水平宽铅垂高。如图：

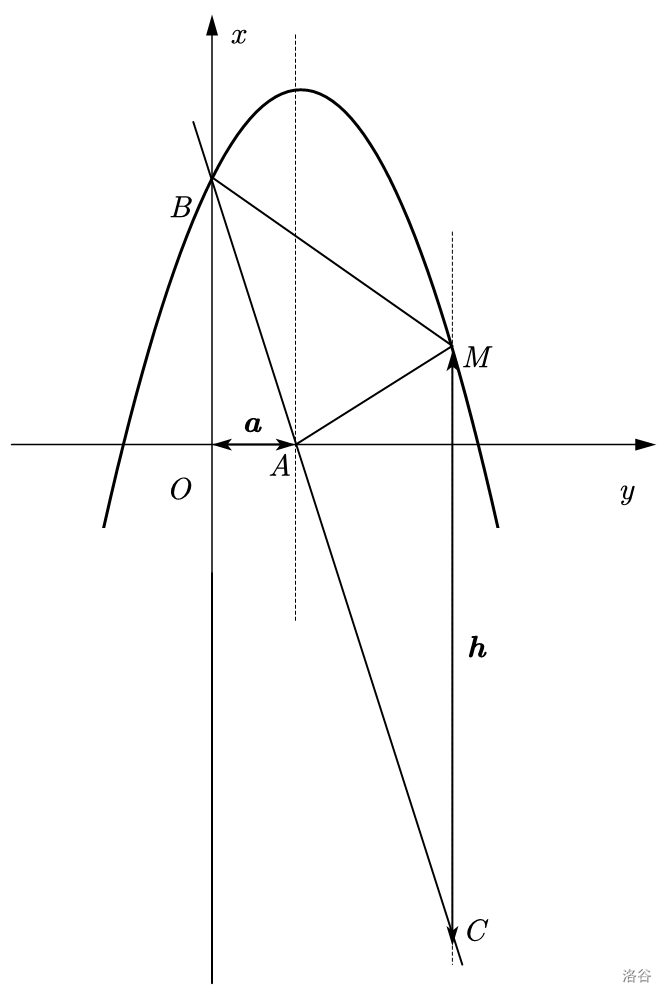
已知 \(C(m,-3m+3),M(m,-m^2+2m+3)\)。所以：

\[MC=\boldsymbol{h}=|y_M-y_C|=-m^2+2m+3+3m-3=-m^2+5m \]

又因为 \(\boldsymbol{a}=OA=1\)，则 \(S\) 与 \(m\) 的函数表达式为：

\[S=\frac{1}{2} \boldsymbol{ah}=\frac{1}{2} \times 1 \cdot (-m^2+5m)=-\frac{1}{2}m^2+\frac{5}{2}m \]

所以：

\[S_{\max}=\frac{4ac-b^2}{4a}=\frac{25}{8} \]

我们还可以知道顶点横坐标为 \(x_M=-\frac{b}{2a}=\frac{5}{2}\)，代入 \(C_1\) 得 \(M(\frac{5}{2},\frac{7}{4})\)。

接下来看最后一问。这是一道等积转化题。我们知道，当两个数的成绩为定值时，一个量为最大值，另一个量就一定为最小值。我们可以从这个地方入手。

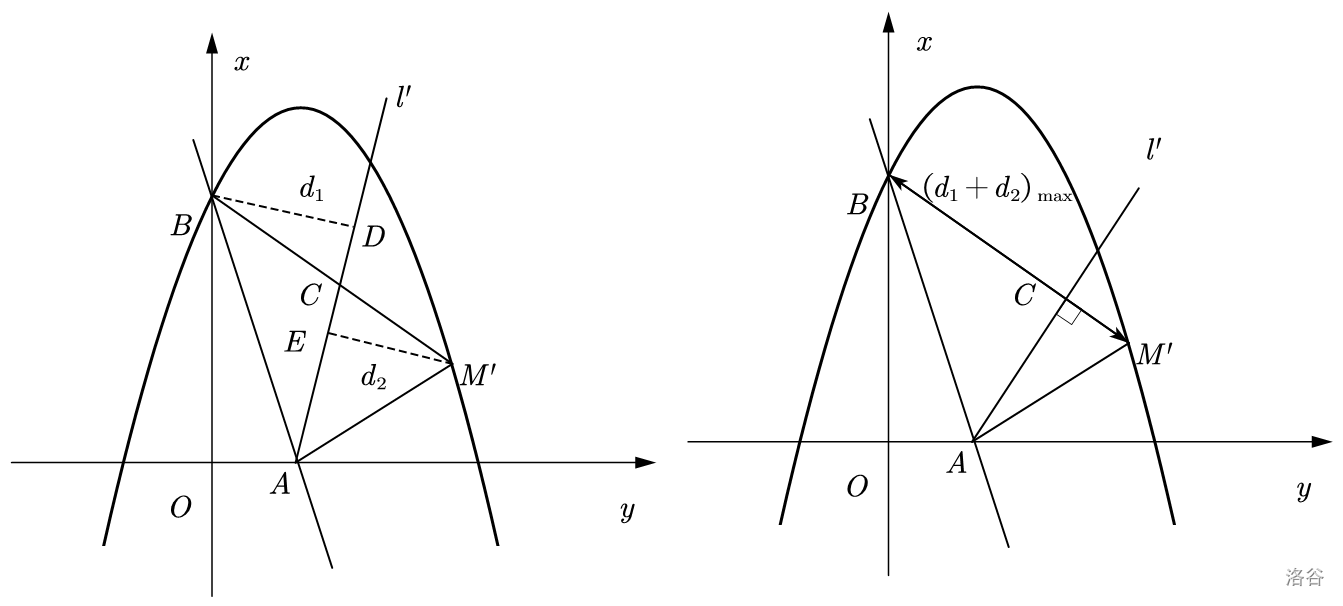
如前图，可得 \(S_{\triangle ABM'}=\frac{1}{2}AC \cdot (d_1+d_2)\)。

所以，当 \(AC=AC_{\min}\) 时，\((d_1+d_2)\) 有最大值。

显然，垂线段最短。我们要求 \(S_{\triangle ABM' \ } BM'\) 边上的高。

因为 \(B(0,3),M'(\frac{5}{2},\frac{7}{4})\)。

所以：

\[BM=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}=\sqrt{(0-\frac{5}{2})^2+(3-\frac{7}{4})^2}=\frac{5\sqrt{5}}{4} \]

所以：

\[AC_{\min}=\frac{2S}{BM'}=\sqrt{5},\cos \angle BAC=\frac{\sqrt{2}}{2} \]

所以 \(\angle BAC=45°\)。

【番外篇】多变形内的水平宽铅垂高

如上图，这是一个不规则四边形，考虑他的水平宽铅垂高。

我们可以将其分成若干个三角形，分别求水平宽铅垂高。

但是上图显然看不出什么，我们可以用它们的公共边上两个定点的投影长度叫做水平宽。两个三角形的第三点分别交公共边所在的直线与一点。我们将第三点和交点的距离之和称为铅垂高。如下图：

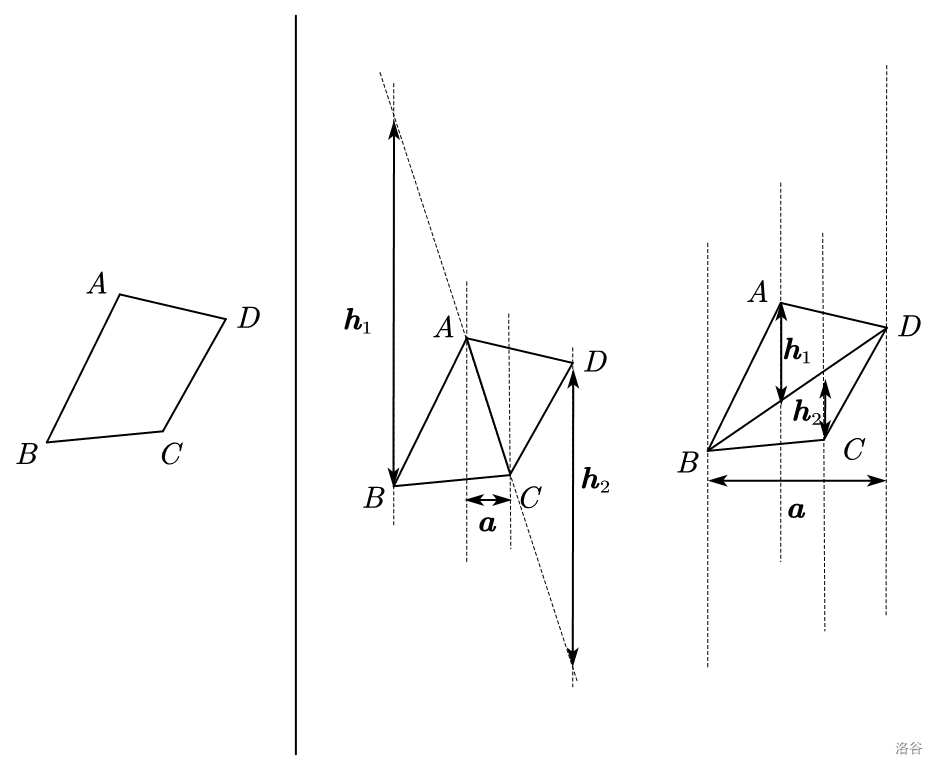
类比第一节的定义，对于一个普通四边形，有如下定义和定理：

• 定义 5.1 四边形的水平宽：四边形的任意一条对角线上的两个顶点的投影长度。记作 \(\boldsymbol{a}\)。

• 定义 5.2 四边形的铅垂高：分别过四边形另外两个顶点作水平宽的垂线，分别交该对角线所在的直线为一点。这两组点的距离分别记作 \(\boldsymbol{h_1,h_2}\)。这两组点的距离之和是该四边形的铅垂高，记作 \(\boldsymbol{h_1+h_2}\)。

• 则有定理 5.1：

\[S_{四边形 ABCD}=\frac{1}{2} \boldsymbol{a \cdot (h_1+h_2)} \]

• 证明：
  由第一节中三角形水平宽铅垂高定理可得：

  \[\begin{align*} S_{四边形 ABCD} &= S_{\triangle ABC}+S_{\triangle ACD}\\ &= \frac{1}{2} \boldsymbol{ah_1} + \frac{1}{2} \boldsymbol{ah_2} \\ &= \frac{1}{2} \boldsymbol{a} \boldsymbol{(h_1+h_2)} \end{align*} \]

由此，我们还可以推广到 \(n\) 边形的水平宽铅垂高，但因初中对多边形面积的考察不是很多，因此不再赘述。

注：因为目前能找到的求多边形面积的题少之又少，并且大多都出现在近年来的中考中，而七八年级没有涉及到，所以放在这个地方。

例 5（2024·济南）【多边形】

在平面直角坐标系 \(xOy\) 中,抛物线 \(C_1:y=x^2+bx+c\) 经过点 \(A(0,2),B(2,2)\)，顶点为 \(D\)；抛物线 \(C_2:y=x^2 - 2mx+m^2 - m + 2 (m \neq 1)\)，顶点为 \(Q\)。

• 求抛物线 \(C_1\) 的表达式及顶点 \(D\) 的坐标；

• 如图 \(1\)，连接 \(AD\)，点 \(E\) 是抛物线 \(C_1\) 对称轴右侧图象上一点，点 \(F\) 是抛物线 \(C_2\) 上一点，若四边形 \(ADFE\) 是面积为 \(12\) 的平行四边形，求 \(m\) 的值；

• 如图 \(2\)，连接 \(BD,DQ\)，点 \(M\) 是抛物线 \(C1\) 对称轴左侧图象上的动点(不与点 \(A\) 重合)，过点 \(M\) 作 \(MN \parallel DQ\) 交 \(x\) 轴于点 \(N\)，连接 \(BN,DN\)，求 \(\triangle BDN\) 面积的最小值。

看第一问，带入坐标得 \(C_1:y=x^2-2x+2\)。可求得 \(D(1,1)\)。

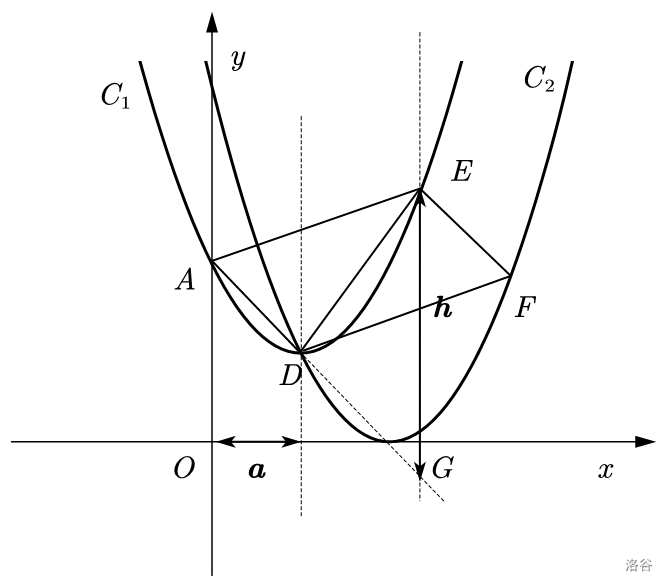
注意：这个时候给出了平行四边形四个点的顺序，所以情况有且只有一种。

我们看第二问，因为所求是一个平行四边形，所以我们可以用水平宽铅垂高求 \(S_{\triangle ADE}\) 的面积。然后乘二即可。

首先求出 \(l_{AD}:y=-x+2\)，设 \(G(n,-n+2),E(n,n^2-2n+2)\),可以表示出:

\[\boldsymbol{h}=EG=y_E-y_G=n^2-2n+2+n-2=n^2-n \]

又因为 \(\boldsymbol{a}=1\) 所以可列方程：

\[2 \times \frac{1}{2} (n^2-n) \cdot EG=12 \]

解得 \(n_1=4,n_2=-3\)（舍去）。所以可得 \(E(4,10)\)。

我们接下来可以通过中点坐标公式求得 \(F(5,9)\)。将改点坐标代入 \(C_2\)，得 \(m_1=2,m_2=9\)。

接下来看第三问，注意：第二问的结果 \(m\) 不能用。

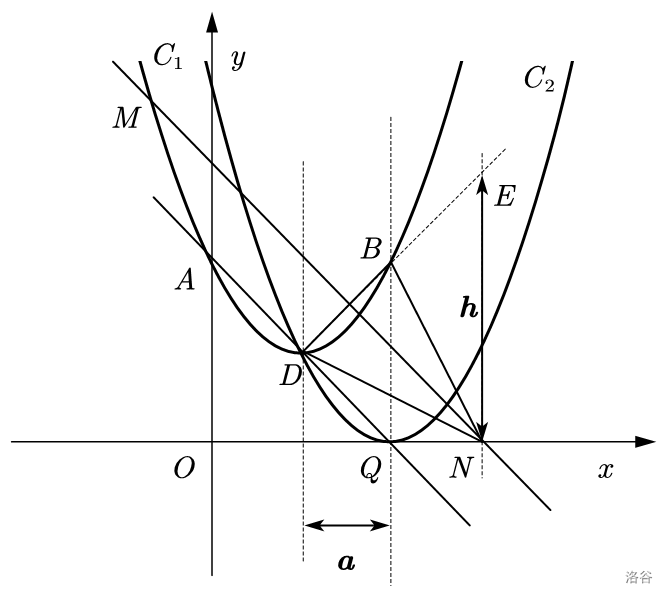
考虑求 \(l_{DQ},l_{MN}\) 的函数表达式。

根据顶点坐标公式 \((-\frac{b}{2a},\frac{4ac-b^2}{4a})\)，可以求出 \(Q(m,-m+2)\)。

根据 \(A,Q\) 两点的左边，求出 \(l_{DQ}:y=-x+2\)。

因为 \(l_{DQ} \parallel l_{MN}\)，所以 \(k_{DQ}=k_{MN}=-1\)。所以 \(l_{MN}=-x+b\)。

设点 \(M(n,n^2-2n+2)\)，将 \(M\) 代入 \(l_{MN}=-x+b\)，解得 \(b=n^2-n+2\)。

所以 \(l_{MN}:y=-x+n^2-n+2\)，可得 \(N(n^2-n+2,0)\)。

我们还可以得出 \(l_{DB}:y=x\)，所以 \(E(n^2-n+2,n^2-n+2)\)。所以：

\[\boldsymbol{h}=EN=n^2-n+2,\boldsymbol{h}_{\min}=\frac{4ac-b^2}{4a}=\frac{7}{4} \]

又因为 \(\boldsymbol{a}=1\)，所以：

\[S_{\triangle BDN \min}=\frac{1}{2} \boldsymbol{ah}_{\min}=\frac{7}{8} \]

例 6（2025·任丘市模拟）【多边形】

如图 \(1\)，抛物线 \(C_1:y=x²+bx+c\) 经过点 \(A(-3,0)\) 和点 \(B(1,0)\)，抛物线 \(C_2\) 与 \(C_1\) 关于原点 \(O\) 成中心对称.

• 求 \(b,c\) 的值；
• 求抛物线 \(C_2\) 的解析式；
• 将抛物线 \(C_2\) 向上平移 \(2\) 个单位长度得到 \(C_3\)，抛物线 \(C_1\) 与 \(C_3\) 相交于 \(P,Q\) 两点（点 \(P\) 在点 \(Q\) 的左侧），如图 \(2\)。
  • 求点 \(P\) 和 \(Q\) 的坐标；
  • 若点 \(M,N\) 分别为抛物线 \(C_1\) 和 \(C_3\) 上 \(P,Q\) 之间的点（点 \(M,N\) 均不与点 \(P,Q\) 重合），直接写出四边形 \(PMQN\) 面积的最大值。

对于一二问，直接代入求值即可。求得 \(C_1:y=x^2+2x-3\)，\(C_2:y=-x^2+2x+3\)。

对于第三问，我们求得 \(C_3:y=-x^+2x+5\)。然后联立：

\( \begin{cases} C_1:y=x^2+2x-3 \\ C_3:y=-x^+2x+5 \end{cases} \) 可得 \(P(-2,-3),Q(2,5)\)。

对于最后一问就可以使用 4.1中的定理 了。

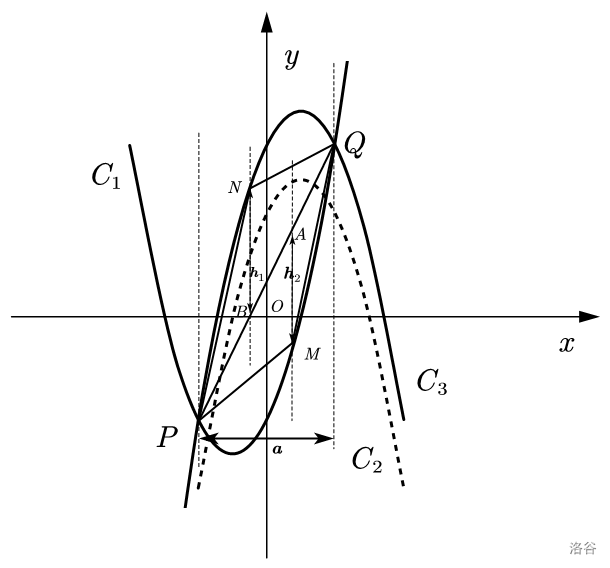
我们作四边形的水平宽铅垂高，可得 \(\boldsymbol{a}=|x_P-x_Q|=4,l_{PQ}:y=2x+1\)。

所以我们设：

\[M(m,m^2+2m-3),A(m,2m+1),B(n,2n+1),N(n,-n^2+2n+5) \]

所以：

\[\boldsymbol{h_1}=AM=|y_A-y_M|=2m+1-m^2-2m+3=-m^2+4 \]

\[\boldsymbol{h_2}=BN=|y_B-y_N|=-n^2+2n+5-2n-1=-n^2+4 \]

所以：

\[(\boldsymbol{h_1+h_2})_{\max}=2 \times \frac{4ac-b^2}{4a}=4+4=8 \]

所以：

\[S_{四边形PMQN}=\frac{1}{2}\boldsymbol{a}(\boldsymbol{h_1-h_2})_{\max}=16 \]

后记

\(\texttt{Update on 2025.7.3}\) 水平宽铅垂高定义性质极其证明

\(\texttt{Update on 2025.7.22}\) 前置知识

\(\texttt{Update on 2025.7.5}\) 水平宽铅垂高和一次函数

\(\texttt{Update on 2025.8.10-8.14}\) 水平宽铅垂高和二次函数、反比例函数

\(\texttt{Update on 2025.8.15}\) 【番外篇】多边形内的水平宽铅垂高

• 以上是水平宽铅垂高的全部内容。其涵盖了初中三年基本所有的关于平面直角坐标系内求三角形面积的题的类型。

• 本文所有的例题（标作者原创的除外）都来自菁优网。许多题具有多解性，水平宽铅垂高只是许多方法中的一种。如果想要看题目的官方解法，在该网站上搜索题目来源即可。至于水平宽铅垂高是不是最优解，相信读者自有定论。

• 求三角形面积还有许多方法，如鞋带公式和本文中提到的平行线转移法，读者可以自行探究。

• 因笔者水平有限，未能对这类问题进行更深层次的研究，仅是将它们汇总。希望文章
  提出的方法能够在更多场合找到用武之地，也希望文章能够对读者提供帮助。