题解：P10892 SDOI2024

题解：P10892 SDOI2024

题目传送门

题目思路

通过阅读题面，我们可以看出，其实对于每一次纠结，如果交出了 \(\frac{n-1}{2}\) 只猫猫，则剩下的为 \(\frac{n+1}{2}\) 只猫猫；如果交出了 \(\frac{n+1}{2}\) 只猫猫，则剩下的为 \(\frac{n-1}{2}\) 只猫猫。
为了使纠结的次数尽可能小，我们要交出为奇数的那一个数，留下为偶数的那一个数。
实际上，我们只需要判断 \(\frac{n-1}{2}\) 和 \(\frac{n+1}{2}\) 的奇偶性即可。如果 \(\frac{n-1}{2}\) 是一个奇数，那就交出，将 \(n\) 的值更新为 \(\frac{n+1}{2}\) 即可，然后令计数器自加。以此类推，直到剩下的猫猫数量为 \(0\) 。
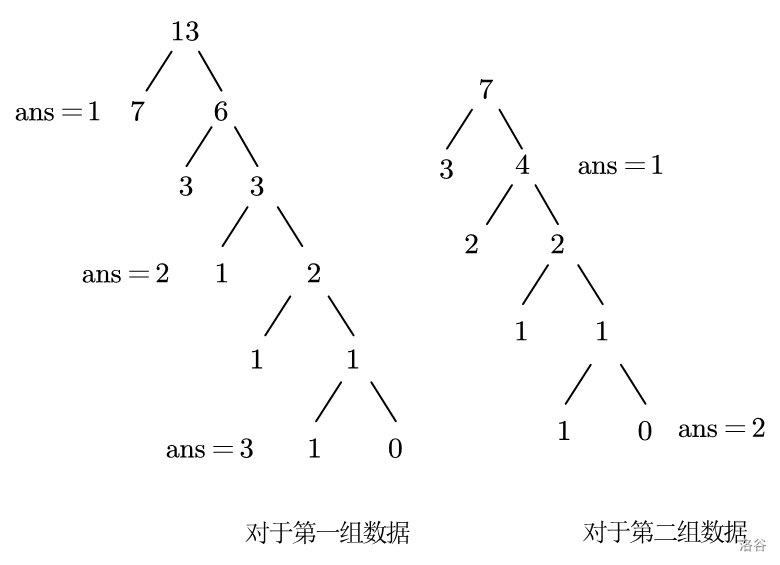
以样例一为例，我们可以画一个树状图来模拟：

代码实现

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll T,tem;
ll n;
int main(){
	cin>>T;
	for(int i=1;i<=T;i++){
		cin>>n;
		ll ans=0;
		while(n>0){ 
			if(n%2!=0){
				ans++;
				if(((n+1)/2)%2==0){
					n=(n+1)/2;
				} 
				else if(((n-1)/2)%2==0){
					n=(n-1)/2;
				}
			}
			if(n%2==0){
				n=n/2;	
			} 
		}
		cout<<ans<<endl;
	}
	return 0;
}