[强化学习论文笔记(5)]:PER

Prioritized Experience Replay: PER

论文地址

PER

笔记

PER的基本思路跟传统强化学习里面的Prioritized Sweeping基本一样。就是从replay buffer中sample的时候按照优先级sample,优先级用transition 的TD-error来表示。transition 的TD-error越大说明这个需要更好的学习。

但是具体到sample的细节。还是需要注意一下的。

greedy TD-error prioritization

显然就是按照TD-error的大小从大到小选。显然这样是有问题的，后面TD-error小的很难被选到,数据利用效率低。 然后另一个缺点就是不够稳定。TD-error是很noisy的.

stochastic prioritization

按照TD-error，按比例依概率选择。\(\alpha\)来调节优先级到底起多少作用。

\[P(i)= \frac{p_i^\alpha}{\sum_k p_k^{\alpha}} \]

\(p_i\)可以是\(|\delta_i|+\epsilon\)(proportional variant);或者是\(\frac{1}{rank(\delta_i)}\) (rank variant)

rank variant

在replay memory中如果要使用rank variant 来sample
[TODO]

proportional variant

在replay memory中如果要使用proportional variant 来sample, 数据结构使用的sum-tree

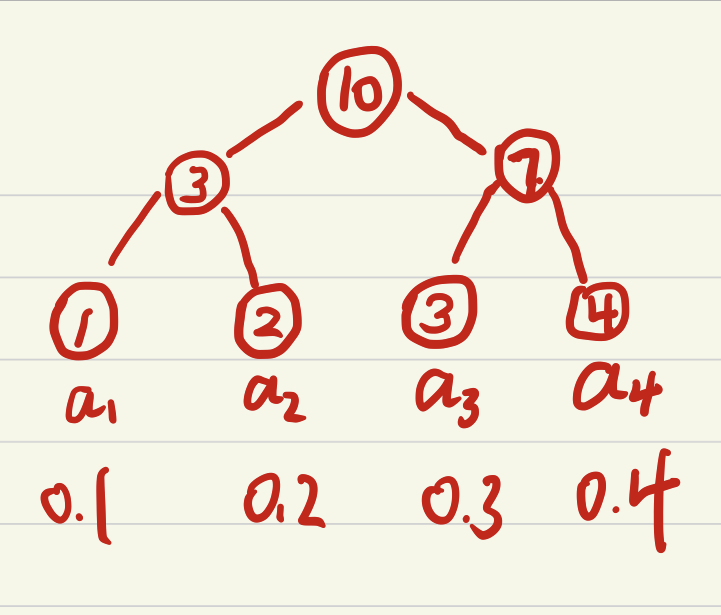
sum-tree提供了一种很优雅的实现按权重sample的方式，数据全部放到叶节点，非叶节点的权重是所有子节点之和。

根节点的权重是所有叶子点的和\(P_{all}\),所以从\([0;P_{all}]\)中随机抽取一个权重，然后去sum-tree中找到对应的叶子节点就能够完成一次随机按比例的随机抽样。

找到对应权重\(w\)的叶子节点的规则就是，比左子节点权重\(w_l\)小，去左子节点，比左子节点大，\(w=w-w_l\)然后去右子节点.直到抵达根节点。

论文中实现的时候是，假如一个batch的size是k,先将\([0,P_{all]\)均分成k段，然后在每一段中采样。

重要性采样IS

事实上按照权重优先级采样打破了数据原本的分布。需要修正每个样本的权重，计算权重的公式如下：

\[w_i = (\frac{1}{N}\cdot \frac{1}{P(i)})^{-\beta} \]

相当于\(E_{norm}[x] = E_P[\frac{1}{N} \cdot \frac{1}{P(x)}x]\)

\(\beta\)是用来调节修正程度的,初始时不稳定，\(\beta\)小一些，直到最后趋近1.

比如对某这个样本,加入取得它的概率是１即\(P(i)＝１\)，\(w_i\)需要很小来降低这个样本的影响，此时\(w_i=N^\beta\)。所以\(\beta\)小，修正大。

实现上: \(w_j = \frac{w_j }{\underset{i}{max}(w_i)}\). 这是为了normalize。

但是论文里说这个是weighted IS. 有点疑惑？

伪代码