机器学习第三天--程序优化

就第二天对数据处理的程序显得十分臃肿，语句代码复用率差，不便于深刻理解，

因此，对程序进行了优化

#coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
"""网络流量使用的数据分析"""

def play_model(x,y,models,mx=None,ymax=None,xmin=None):
    '''
    编写函数是可根据需要添加参数
    本例的设计步骤：
         1.先做出绘制原始数据散点图的函数
         2.根据需要添加添加绘制拟合后需要的方式
    :param models: 返回线性拟合方式组成的列表
    :param mx: 采样点数的设置
    :param ymax: 限制y轴的最大呈现值
    :param xmin: 设置x轴起始参数
    '''
    plt.clf()
    plt.scatter(x,y,s=10)
    plt.title("Wbe traffic over the last month")
    plt.xlabel("Time")
    plt.ylabel("Hits/hour")
    #xticks(a,b)在a的位置贴上标签b
    plt.xticks([w*7*24 for w in range(10)],["week %i"%w for w in range(10)])
    #做拟合曲线
    if models:
        if(mx==None):
            mx=np.linspace(0,x[-1],1000)
        #zip返回的是相应元素组成的列表
        for model,linestyle,color in zip(models,linestyles,colors):
            plt.plot(mx,model(mx),linestyle=linestyle,linewidth=2,c=color)
        plt.legend(["d=%i"%m.order for m in models],loc="upper left")
    #自动调整图像显示的比例
    plt.autoscale(tight=True)
    plt.ylim(0)
    if ymax:
        plt.ylim(ymax=ymax)
    if xmin:
        plt.xlim(xmin=xmin)
    plt.grid()
    plt.show()

def error(f,x,y):
    '''
    计算误差
    :param f:拟合后的函数值
    :param x: 拟合曲线在实际数据中的取值
    :param y: 实际数据值
    '''
    return(np.sum((f(x)-y)**2))

if __name__=="__main__":
    # 获取数据
    linestyles=['-','--',':','-.','--']
    colors=['g','k','b','r','m']
    data=np.genfromtxt("F:\SOFT DOWNLOAD\\1400OS_Code\\1400OS_01_Codes\data\web_traffic.tsv",delimiter="\t")
    #利用特殊索引将获取的二维数据进行分割
    x=data[:,0]
    y=data[:,1]
    #判断在数据中是否有无效数据

    x = x[~np.isnan(y)]
    y = y[~np.isnan(y)]


    #play_model(x,y,None)
    #进行多阶拟合
    fp1=np.polyfit(x,y,1)
    f1=np.poly1d(fp1)
    fp2=np.polyfit(x,y,2)
    f2=np.poly1d(fp2)
    fp3=np.polyfit(x,y,3)
    f3=np.poly1d(fp3)
    fp4=np.polyfit(x,y,10)
    f4=np.poly1d(fp4)
    fp5=np.polyfit(x,y,50)
    f5=np.poly1d(fp5)
    play_model(x,y,[f1,f2,f3,f4,f5])
    for i in [f1,f2,f3,f4,f5]:
        print(error(i,x,y))

结果为

       

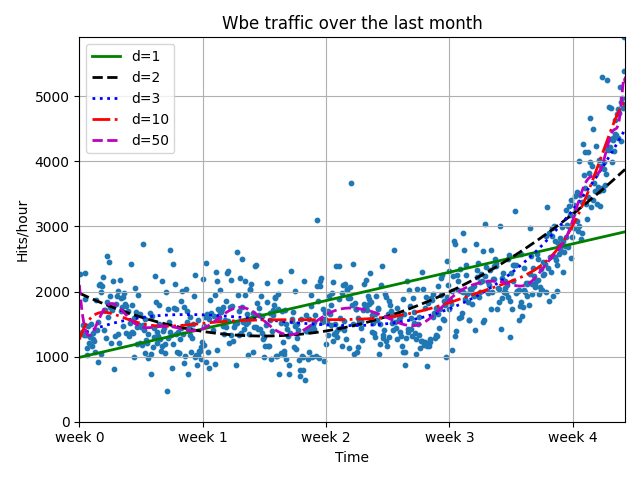
将数据扩展

 mx = np.linspace(0 * 7 * 24, 6 * 7 * 24, 100)
    play_model(x,y,[f1,f2,f3,f4,f5],mx,ymax=10000,xmin=0*7*24)

结果

 

 

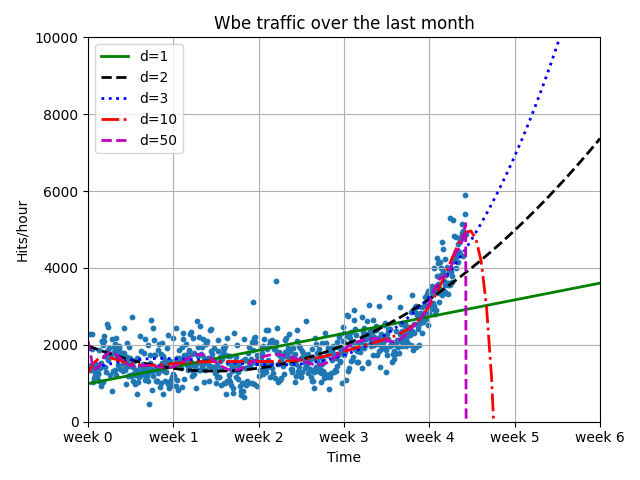
 当得到此图后发现并不能无论拟合的阶数是多少，都无法的到一个较好的模型去解释这个数据未来的走向

因此我们利用其转折点前后的数据进行拟合,三阶误差最少

    x = x[~np.isnan(y)]
    y = y[~np.isnan(y)]

    #采用转折点后的数据进行拟合
    turn=int(3.5*7*24)
    xa=x[turn:]
    ya=y[turn:]

    #play_model(x,y,None)
    #进行多阶拟合
    fp1=np.polyfit(xa,ya,1)
    f1=np.poly1d(fp1)
    fp2=np.polyfit(xa,ya,2)
    f2=np.poly1d(fp2)
    fp3=np.polyfit(xa,ya,3)
    f3=np.poly1d(fp3)
    fp4=np.polyfit(xa,ya,10)
    f4=np.poly1d(fp4)
    fp5=np.polyfit(xa,ya,50)
    f5=np.poly1d(fp5)
    mx = np.linspace(0 * 7 * 24, 6 * 7 * 24, 100)
    play_model(x,y,[f1,f2,f3,f4,f5],mx,ymax=10000,xmin=0*7*24)
    for i in [f1,f2,f3,f4,f5]:
        print(error(i,x,y))

 

 

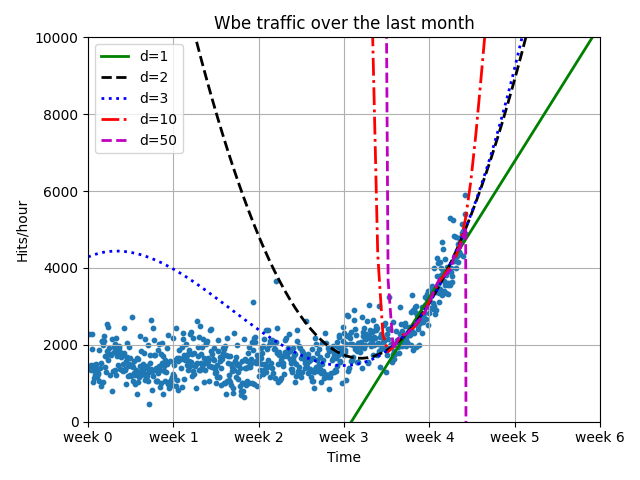
 误差数据为：

30035502983.24833
54112491928.51646
1897459097.0429592
3.699240506614672e+21
1.7321217468080033e+25

 当得出最小误差后拟合后，我们即可对数据进行预测。