Catalan数

理论理解

一般问题大都可以转换为：

一个有n个1和n个-1组成的字串，且前k个数的和均不小于0那这种字串的总数为多少？

至于为什么总的方案（不考虑合不合法）是\(C(2n,n)\)相当于在一共2n次操作中选n次向上的方案数，
不合法的方案数，同理可得：

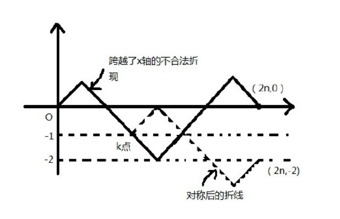
能到达(2n,-2)点的次数，满足在总共2n次操作下选(n+1)次向下的，（或者说选(n-1)次向上的）也就是\(C(2n,n+1)\)。所以答案就是：
\(C(2n,n)-C(2n,n+1)\)或者\(C(2n,n)-C(2n,n-1)\)。

一些公式的转换：

做题

P1375 小猫
算是板子吧，等同于多边形三角剖分问题 $$\sum_{k=0}^{n} \ f(k)∗f(n−k+1) $$就是上面的公式三，可以转换。但要用乘法逆元，就有点麻。

P3200 [HNOI2009] 有趣的数列
相当于给定一个有序数列，每次从头取，选择依次放在偶数位，还是奇数位，因为偶数位一定比此前的所有数大（由题得），所以可证，选择的偶数位一定不比奇数位多，但模数不保证为质。