P3195 [HNOI2008] 玩具装箱 & 斜率优化

from DP...

原来一直阻碍我学习斜率优化的是原转移方程推不出来呀。

终于鼓起勇气来学斜率优化了。

问题描述

• 有 \(n\) 个玩具，每个玩具长度为 \(c_i\)
• 需要将玩具分成若干组，每组包含连续的玩具
• 对于一组玩具从 \(i\) 到 \(j\)，容器长度 \(x\) 计算为：
  \[x = \sum_{k=i}^{j} c_k + (j - i) \]
  其中 \(j - i\) 是玩具之间的空隙数量
• 容器的制作成本为 \((x - L)^2\)，其中 \(L\) 是给定常数
• 目标：最小化总成本

原转移方程

定义 \(dp[i]\) 为前 \(i\) 个玩具的最小总成本。最终答案是 \(dp[n]\)。

为了计算 \(dp[i]\)，考虑最后一组玩具的结束位置，相当于针对每个需计算的 \(dp[i]\) 枚举它最后一个的分组情况。假设最后一组是从 \(j\) 到 \(i\)（其中 \(1 ≤ j ≤ i\)），那么：

• 前 \(j-1\) 个玩具的最小成本为 \(dp[j-1]\)
• 最后一组（从 \(j\) 到 \(i\)）的成本为 \(cost(j, i)\)

因此：

\[dp[i] = \min_{1 ≤ j ≤ i} \{ dp[j-1] + cost(j, i) \} \]

计算 \(cost(j, i)\)

根据容器长度公式：

\[x = \sum_{k=j}^{i} c_k + (i - j) \]

成本为：

\[cost(j, i) = (x - L)^2 = \left( \sum_{k=j}^{i} c_k + (i - j) - L \right)^2 \]

引入前缀和数组 \(s\)，其中 \(s[i] = \sum_{k=1}^{i} c_k\)，那么：

\[cost(j, i) = \left( (s[i] - s[j-1]) + (i - j) - L \right)^2 \]

因此，转移方程变为：

\[dp[i] = \min_{1 ≤ j ≤ i} \{ dp[j-1] +\left(s[i] + i - s[j-1] - j - L \right)^2\} \]

斜率优化

化式子

关于原转移方程，将其变为：

\[dp[i] = \min_{0 ≤ j < i} \{ dp[j] +\left(s[i] + i - s[j] - j - (L + 1) \right)^2\} \]

定义新数组 \(t[i] = s[i] + i\)，并令 \(C = L+1\)，则：

\[dp[i] = \min_{0 ≤ j < i} \{ dp[j] + (t[i] - t[j] - C)^2 \} \]

其中：

• \(t[i] = s[i] + i\)
• \(s[i]\) 是前缀和（\(s[0] = 0\)，所以 \(t[0] = 0\)）
• \(C = L+1\)

首先将平方项展开：

\[dp[i] = \min_{0 ≤ j < i} \{dp[j]+t[i]^2-2t[i]t[j]-2t[i]C+t[j]^2+2t[j]C+C^2\} \]

再合并：

\[dp[i] = \min_{0 ≤ j < i} \{t[i]^2-2t[i]t[j]-2t[i]C+(t[j]+C)^2\} \]

将与 \(j\) 无关的项分离出来：

\[dp[i] = \min_{0 ≤ j < i} \{dp[j]+(t[j]+C)^2-2t[i]t[j]\}+t[i]^2-2t[i]C \]

问题转换

我们定义两个新函数：

1. \(X(j) = t[j]\)
2. \(Y(j) = dp[j] + (t[j] + C)^2\)

代入后：

\[dp[i] = \min_{0 \leq j < i} \{ Y(j) - 2t[i]X(j) \} + t[i]^2 - 2t[i]C \]

现在，关键来了！

为什么要这样定义，发现方程中要求 $Y(j) - 2t[i]X(j) $，那么假设 \(Y(j) - 2t[i]X(j)=b\)，那么 \(Y(j)=2t[i]X(j)+b\)。

将 \(k\) 设为 \(2t[i]\)，发现 \(Y(j)=kX(j)+b\) 不就是一条经过 \((X(j),Y(j))\) 斜率为 \(k\)，截距为 \(b\) 的直线吗？

所以 \(Y(j)-kX(j)\) 是什么，就是一条经过 \((X(j),Y(j))\) 斜率为 \(k\) 的直线与 \(y\) 轴的交点（的横坐标）。

所以问题：

\[\min_{0 \leq j < i} \{ Y(j) - 2t[i]X(j) \} \]

就等价于：
对于每个 \(dp[i]\) 找到一个点 \((X(j), Y(j))\)，使得斜率为 \(2t[i]\) 的直线经过该点时，在 \(y\) 轴上的截距最小，它对答案的贡献就是这个最小截距。

开始优化

针对每个 \(dp[i]\)，要使它候选决策点 \((X(j), Y(j))\) 对他的贡献最小，肯定要使直线的截距更小。但每个 \(i\) 不定，它的斜率 \(k\) 也就是 \(2t[i]\) 也不定，那怎样才能维护出一个正确的最优节点呢？

最优点集

假设一张图上有一些点，我们想让它们在未知斜率的情况下截距最小，那么哪些点可能会是最小的呢？

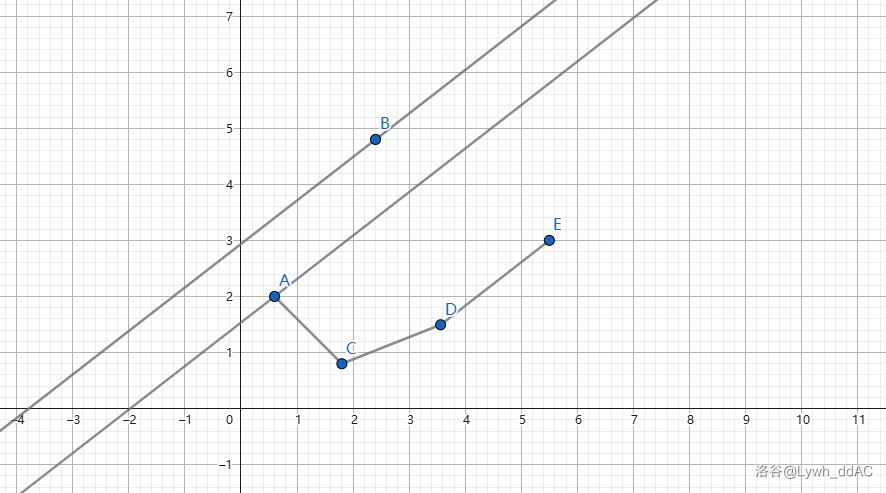
虽然不知道斜率是多少，但我们知道斜率的正负（\(2t[i]\) 肯定为正），也就是直线成上升趋势，我们发现，如果此时有多个点，未知斜率直线的最小截距，只有可能在经过 A，C，D，E 的直线上产生，也就是最优点不可能是 B 点，因为不管一条斜率为多少（不为负）的直线经过 B 它的截距一定比同斜率经过 A 点的直线大。

所以不在凸包上的一定不会为最优点，而且在凸包上的也不一定为最优点，比如说 A 点和 C 点，在 C 点被算出来之前，A 点是最优点，而在 C 点被算出来以后，A 点将永远不会成为最优点。

而且针对不同斜率，最优点也是不一样的，比如斜率稍大时可能 E 点是最优点，而当斜率稍小时 C 有可能成为最优点。所以这就是为什么说要先维护一个最优点集而不是一个最优点。

那这个点集该怎么维护呢？

发现：对于三个点 \(A = (X_a, Y_a)\), \(B = (X_b, Y_b)\), \(C = (X_c, Y_c)\)，如果 \(B\) 在 \(A\) 和 \(C\) 连线的上方，那么 \(B\) 不在凸包上。

数学上，这可以通过斜率来判断：

• 如果 \(\frac{Y_b - Y_a}{X_b - X_a} \geq \frac{Y_c - Y_b}{X_c - X_b}\)，那么 \(B\) 不在凸包上

翻译过来就是，如果 \(AB\) 的斜率大于 \(BC\) 的斜率那么 \(B\) 不在凸包上。

如何维护

当我们计算完 \(dp[i]\) 后，我们得到一个新点 \((X(i), Y(i))\)。我们需要将这个点添加到凸包中。假设我们已经有凸包上的点序列：\(P_1, P_2, ..., P_m\)（按 \(X\) 坐标排序）

当我们添加新点 \(P_{new}\) 时，需要检查最后三个点 \(P_{m-1}, P_m, P_{new}\) 是否满足凸包性质。

判断条件：

• 如果 \(\text{slope}(P_{m-1}, P_m) \geq \text{slope}(P_m, P_{new})\)，那么 \(P_m\) 不在凸包上，应该被移除
• 反之直接添加即可

$\text{slope}(A,B) $ 表示直线 AB 的斜率。

若移除 \(P_m\) 后，我们需要继续检查 \(P_{m-2}, P_{m-1}, P_{new}\)，直到满足凸包性质。

实现起来也相对简单，拿一个数组来存当前凸包上的值，照着上面维护就行了。

	while(End>=1){
        if(slope(tb[End-1],tb[End])>=slope(tb[End],i))
        End--;
		else
			break ;
    }
	tb[++End]=i;

其实为什么是 while(End>=1)还有点不懂。

一个大概的解释是：

既然进来一个点要检查他前两个点，那当 \(End=1\) 意味着要比较 \(tb[0]\)，\(tb[1]\) 和 \(i\) 点，这说明原点还有一条连向凸包的边。

所以说，维护出来的凸包将会是一条过原点的曲线，那么上面说的“在 C 点被算出来以后，A 点将永远不会成为最优点”实际上 A 点已经不在凸包上了？线段 AC 将被移除，取而代之的是一条由原点连向 C 点的线段。

但实际上是没有这条线段的，只是为了更改第一个点。

最优点

好了，现在最优点集维护出来了，那怎么找出上面最优的点呢？

二分查找

这是一个通用的写法。

已知当前直线斜率为 \(2t[i]\)，如何找到最优点使得截距最小?

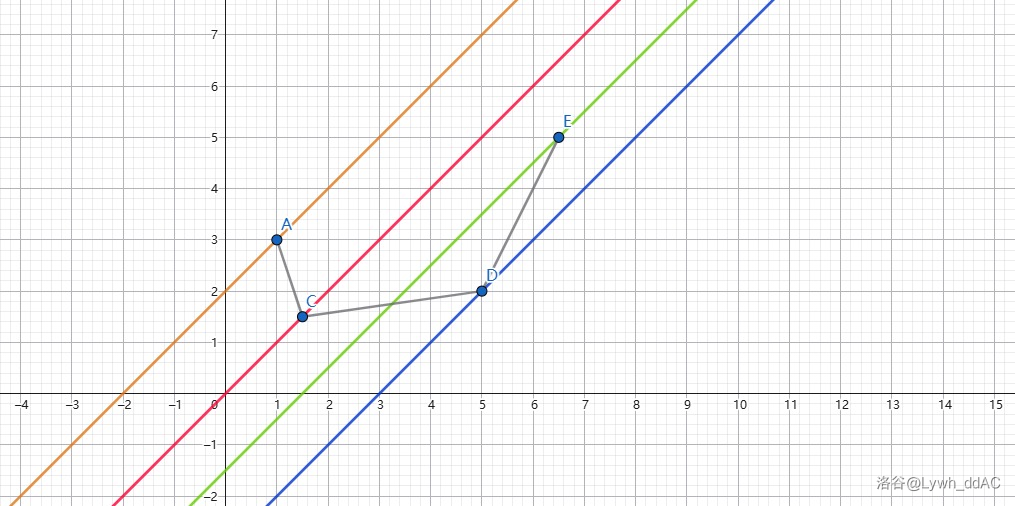
如图，当前斜率为 \(k\) 的凸包上的点有四条，肉眼可见蓝色直线的斜率最低，那 D 点是怎么找出来的呢？

对于给定的斜率 \(k\)，我们要在凸包上找到那个最优的点 \(j\)，使得：

• \(\text{slope}(j-1, j) < k \leq \text{slope}(j, j+1)\)

也就是当 \(j-1\) 到 \(j\) 的斜率比 \(k\) 小，\(j\) 到 \(j+1\) 的斜率比 \(k\) 大时，\(j\) 为最优点。（应该不难理解）

代码也很清新

    int k=2*t[i];
	int l=0,r=End;
	while(l<r){
    	int mid=(l+r)/2;
    	if(slope(tb[mid],tb[mid+1])<k){
    		l=mid+1;
    	}
    	else{
    		r=mid;
       	}
	}
	dp[i]=Y(tb[l])-t[i]*2*X(tb[l])+t[i]*t[i]-2*t[i]*C;;

于是玩具装箱的二分版代码就出来了
::::info[代码]

#include<bits/stdc++.h>
using namespace std;
#define N 50005
#define int long long

int n,L,C,End;
int c[N],sum[N],dp[N],t[N],tb[N];

int X(int i){
	return t[i];
}

int Y(int i){
	return dp[i]+(t[i]+C)*(t[i]+C);
}

float slope(int j,int k){
	return 1.0*(Y(j)-Y(k))/(1.0*(X(j)-X(k)));
}

signed main(){
	cin>>n>>L;
	C=L+1;
	for(int i=1;i<=n;i++){
		cin>>c[i];
		sum[i]=sum[i-1]+c[i];
		t[i]=sum[i]+i;
	}
	memset(dp,0x3f3f3f,sizeof(dp));
	dp[0]=0;
	for(int i=1;i<=n;i++){
		int k=2*t[i];
		int l=0,r=End;
		while(l<r){
			int mid=(l+r)/2;
			if(slope(tb[mid],tb[mid+1])<k){
				l=mid+1;
			}
			else{
				r=mid;
			}
		}
		dp[i]=Y(tb[l])-t[i]*2*X(tb[l])+t[i]*t[i]-2*t[i]*C;;
		while(End>=1){
			if(slope(tb[End-1],tb[End])>=slope(tb[End],i))
				End--;
			else
				break ;
		}
		tb[++End]=i;
	}
	cout<<dp[n];
	return 0;
}

::::

二分查找的话，复杂度还有个 \(log\)，怎样把 \(log\) 给去掉呢？

单调队列