圆方树
从仙人掌讲起吧,例题:P5236 【模板】静态仙人掌
题目要求每次询问两个点 \(u,v\),求两点之间的最短路。
想,如果图只是一棵树,那很简单,用前缀和,用 \(sum[u]+sum[v]-sum[lca(u,v)]\) 简单 \(log(n)\) 求解。
但问题在于题中的图有可能会有环,如果有环,那就无法简单按照树的操作解题,于是想要把环消掉。环,它之所以是环,是因为它有环的性质,那么如果想要合法消掉环,就要保证在消掉环后,原环上的点依然保有原来的性质。
环有什么性质?
圆的。- 环上人两个点都可以通过不相同的两条路(互相)到达。
为了保留以上性质,引入圆方树(说白了就是没有环的图)。定义原先没有在环上的点为圆点,新建的点为方点。所以:
对于每个环,新建一个方点,连接方点和所有环上的点,删掉原环边。
当然此操作等价于重新建一棵树,连接方点和环点,圆点和方点,圆点和圆点。
如此一来图中就没有环了,可新树的边权该怎么设置呢?设出的边权要保证能正确查询任两个点之间的距离。这个后面再说,先建一棵树的框架出来。
圆点怎么找?对于一个 \(u\) 点来讲,如果它所连到的 \(v\) 不经过其父亲节点 \(u\) 能到达的最浅的节点在 \(u\)
之后,也就是 \(low[v]>dfn[u]\),那么这两个点都是圆点,因为两个点都不在环上。所以直接加就行了。
if(low[v]>dfn[u]){
Add(u,v,e[i].w);
Add(v,u,e[i].w);
}
方点怎么找?因为是 \(dfs\) 所以对于一个 \(u\) 点来讲,会一直下探到链结束,如果在这条链的结尾又遍历到了 \(u\),那肯定就形成了一个环,于是要把这一整条链都找一个方点连起来。如何实现呢?其实也不难,在 \(dfs\) 下探的时候记录一下每个节点的前驱,在当前子树搜完后,再遍历一下 \(u\) 节点的每个儿子,如果发现某个儿子 \(v\) 的前驱结点不是 \(u\),那么说明这个儿子肯定是从 \(u\) 其他儿子往下遍历到了的,于是就形成了一个环。像这样:
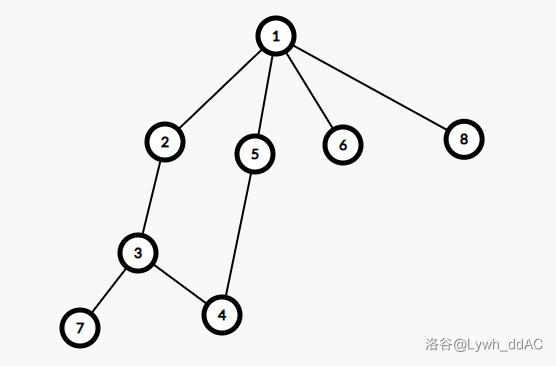
图中在从 \(1\) 往下深搜时会从 \(2\) 到 \(3\) 到 \(4\) 到 \(5\),前缀数组分别就为 \(1\),\(2\),\(3\),\(4\)。于是在搜完 \(1\) 节点后对 \(1\) 的子节点遍历,发现儿子 \(5\) 的前缀不等于 \(1\) 于是断定从 \(2\) 到 \(5\) 这条路径是一条链,所以针对链做操作。
代码:
for(int i=head[u];i!=-1;i=e[i].next){
int v=e[i].to;
if(fa[v]==u||dfn[v]<=dfn[u]) continue ;
slove(u,v,e[i].w);
}
\(fa\) 数组就是记录前驱结点,这个 \(dfn[v]<=dfn[u]\) 保证了不倒回(肯定不能往父亲搜啊)。
接着就是边权问题,我们如下设置边权:
- 若 \(u,v\) 都是圆点,则权值为原图中边权
- 若 \(u\) 为方点,则权值为 \(v\) 到 \(u\) 父亲的最短路
圆点到圆点设为原边权没有问题 ,为什么将圆点到方点的边权设为到方点父亲的最短路呢?思考,给定 \(u\),\(v\),找 \(u\) 到 \(v\) 的最短路径,那他们的 \(lca\) 只有两种情况,如果他们的 \(lca\) 是圆点,可能 \(u\) 到 lca 路径上还会经过一些环,若要穿过环,一定是走环得最短路,假如接入点为 x 那么从 x 走出环一定经过环顶 y,从而最优一定走 x,到 y的最短路(二选一)。
比如:
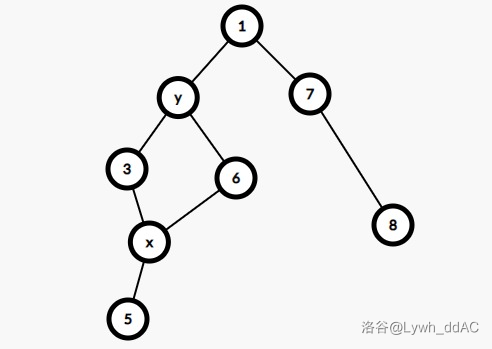
上图如果在 x-3-y-6 之间建一个方点的话,那么方点连接 3,6,x 的边权将都会是到 y 的最短路,于是设边权的问题解决了:
void slove(int u,int v,int w){
// u: 当前DFS节点
// v: 通过非树边连接到的节点(形成环)
// w: 非树边的边权
cc++; // 创建新的方点编号
int cur=v,pre=w;
// 计算环上各节点到参考节点u的顺时针距离
while(cur!=fa[u]){
sum[cur]=pre; // 记录节点i到u的顺时针距离
pre+=ww[cur];
cur=fa[cur];
}
sum[cc]=sum[u]; // 整个环的总长度存到方点上
sum[u]=0;
cur=v;
// 连接方点和环上所有圆点
while(cur!=fa[u]){
int pw=min(sum[cur],sum[cc]-sum[cur]);
Add(cur,cc,pw);
Add(cc,cur,pw);
cur=fa[cur];
}
}
那如果 u,v 的 lca 是方点怎么办呢?那么一定有如 x,z 一样的都在环上的点,如图:
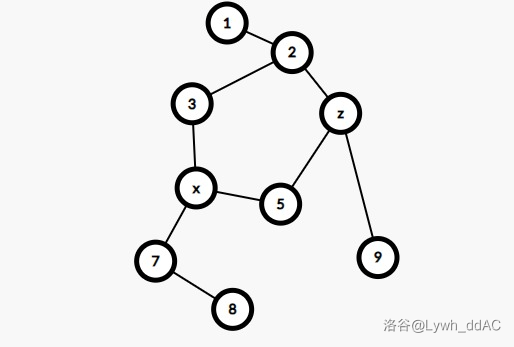
假如求 \(8\) 到 \(9\) 的最短路,\(u=8\),\(v=9\),那么距离就可以转换为,\(u\) 到 \(x\) 的距离,加上 \(v\) 到 \(z\) 的距离,再加上 \(x\) 到 \(z\) 的距离,就是 \(dis(u,x)+dis(v,z)+dis(x,z)\)。
另一个问题 \(dis(x,z)\) 怎么求呢,你在建树时已经求出了每个点在环中顺时针的前缀和,有可能直接从 \(u\) 顺时针到 \(v\),但也有可能反着绕环一圈,从 \(u\) 逆时针到 \(v\),这样用总环长减去顺时针距离再比较一下就行了。
int huanzhi(int a,int b){
return min(abs(sum[a]-sum[b]),sum[p[a][0]]-abs(sum[a]-sum[b]));
}
那这样会不会出现一种情况,就是一个点同时被两个环包含,这样算环距不会出问题吗?实际上是不会的,可以发现要的是,若一个点同时被两个环包含,那该点一定是其中一个环的环顶,因为一个环顶永远不会成为 \(lca\)(显然因为环顶一定某个是方点的父亲)所以永远不会因为一个环顶去求其下的环的长度,一个很简单的证明就是因为出来的圆方树,是一颗树,那么一定不会有一个圆点同时是两个方点的儿子,所以一定有一个方点是圆点儿子。
实现起来,用倍增求出 \(lca\) 的同时求出 \(x\),\(z\) 点,而后正常操作就行了。具体代码:
#include<bits/stdc++.h>
using namespace std;
#define N 500005
int cnt,Cnt,n,m,q,u,v,w,cn,cc,lasta,lastb,top;
int head[N],Head[N],st[N],low[N],dfn[N],vis[N],dep[N],sum[N],ww[N],fa[N],zw[N],p[N][25];
struct L{
int to,next,w;
}e[N*4],E[N*4];
void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].w=w;
e[cnt].next=head[u];
head[u]=cnt;
}void Add(int u,int v,int w){
E[++Cnt].to=v;
E[Cnt].w=w;
E[Cnt].next=Head[u];
Head[u]=Cnt;
}
void slove(int u,int v,int w){
cc++;
int cur=v,pre=w;
while(cur!=fa[u]){
sum[cur]=pre;
pre+=ww[cur];
cur=fa[cur];
}
sum[cc]=sum[u];
sum[u]=0;
cur=v;
while(cur!=fa[u]){
int pw=min(sum[cur],sum[cc]-sum[cur]);
Add(cur,cc,pw);
Add(cc,cur,pw);
cur=fa[cur];
}
}
void tarjan(int u,int Fa){
dfn[u]=low[u]=++cn;
vis[u]=1;
for(int i=head[u];i!=-1;i=e[i].next){
int v=e[i].to;
if(v==Fa) continue ;
if(!dfn[v]){
fa[v]=u;
ww[v]=e[i].w;
tarjan(v,u);
low[u]=min(low[v],low[u]);
}
else{
low[u]=min(low[u],dfn[v]);
}
if(low[v]>dfn[u]){
Add(u,v,e[i].w);
Add(v,u,e[i].w);
}
}
for(int i=head[u];i!=-1;i=e[i].next){
int v=e[i].to;
if(fa[v]==u||dfn[v]<=dfn[u]) continue ;
slove(u,v,e[i].w);
}
}
void dfs(int u,int fa){
dep[u]=dep[fa]+1;
p[u][0]=fa;
for(int i=1;i<=20;i++){
p[u][i]=p[p[u][i-1]][i-1];
}
for(int i=Head[u];i!=-1;i=E[i].next){
int v=E[i].to;
if(v==fa) continue ;
zw[v]=zw[u]+E[i].w;
dfs(v,u);
}
}
int lca(int a,int b){
if(dep[a]>dep[b]) swap(a,b);
lasta=a;lastb=b;
for(int i=20;i>=0;i--){
if(dep[p[b][i]]>=dep[a]){
lasta=b;lastb=b;
b=p[b][i];
}
}
if(a==b) return a;
for(int i=20;i>=0;i--){
if(p[b][i]!=p[a][i]){
b=p[b][i];
a=p[a][i];
}
}
lasta=a;
lastb=b;
return p[a][0];
}
int huanzhi(int a,int b){
return min(abs(sum[a]-sum[b]),sum[p[a][0]]-abs(sum[a]-sum[b]));
}
int main(){
memset(head,-1,sizeof(head));
memset(Head,-1,sizeof(Head));
cin>>n>>m>>q;
cc=n;
for(int i=1;i<=m;i++){
cin>>u>>v>>w;
add(u,v,w);
add(v,u,w);
}
tarjan(1,0);
dfs(1,0);
while(q--){
cin>>u>>v;
int Lca=lca(u,v);
if(Lca>n)
cout<<zw[u]+zw[v]-zw[lasta]-zw[lastb]+huanzhi(lasta,lastb)<<endl;
else
cout<<zw[u]+zw[v]-zw[Lca]*2<<endl;
}
return 0;
}
发现狭义圆方树只是保证了原图的性质与结构,并没有完全展现方点的作用(至少这道题是这样),于是有广义圆方树。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号