根号大人，我爱你～❤
根号大人我喜欢你～
可是每次作完你的题后，都需要调呢～
真是不乖呢～❤
哼哼哼～最后不还是会被我调好～
前言
好了回到正题。不会分块？不会莫队？不会根号分治？没关系！来看这篇文章！
根号是个很优美的数字，如果你 分块/莫队/根号分治 写的多的话，你就会注意到，为了时间复杂度的平衡，根号是个很好的选择。
分块
0. 前言
提到 \(\mathcal{O}(n\sqrt n)\) 想必你想到的第一个就是分块，我个人认为分块不算一种数据结构，而是一种思想，我更愿意称之为一种优美的暴力。（分块一般分为广义分块与狭义分块，以下介绍狭义分块）
1. 例题 & 解析
接下来的例题，按个人认为的难度单调递增。
分块是个很重要的东西，所以分块入门 \(1\dots 9\) 我都会写一遍。
P13976 数列分块入门 1
来看看例题，题意很简单，区间加法与单点查询，显然这个树状数组和线段树都很好写，不过我们还是来看看分块怎么做。
你看，当我们使用暴力时很慢对吧，为什么呢？因为我们每次都要枚举区间来加但这样显然会超时，怎么办呢？
这个时候我们来想想分块，分块分块肯定要分出来一个个块吧，于是你发现，我们将 \(1\dots n\) 分成若干块，区间加的时候就枚举在 \([l,r]\) 这个区间内的块加上。
但是你注意到加完每个块后，肯定有些修改不是一定可以被若干个块刚好覆盖的，于是我们考虑暴力枚举散块，暴力修改，在查询时只需加上这个数本身的值，这个数暴力加的值与这个数属于的块加的值。
容易发现，随着分块的块长变大要加的整块就少，但要暴力枚举的又多了，反之亦然，假设块长为 \(b\) 单次整块修改时间复杂度最多为 \(\mathcal{O}(\frac{n}{b})\)，散块单次修改时间复杂度最多为 \(\mathcal{O}(b)\)，总时间复杂度就为 \(\mathcal{O}(m(b+\frac{n}{b}))\)（跑不满）注意到当 \(b=\sqrt n\) 表达式最小，这个时候时间复杂度为 \(\mathcal{O}(2m\sqrt n)\)。
来看看实现，我习惯记录块长、有多少个块、每个块下标的开始与结束、每个下表属于哪个块，还有些其他的根据题目而定，比如此题，我们就还需要记录每个块加的值。
:::success[Ac Code]
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define _ read<int>()
#define R register
#define rint register int
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=3e5+10;
int a[N],pos[N],add[N],st[N],ed[N];
inline void modify(rint l,rint r,rint v)
{
rint lk=pos[l],rk=pos[r];//l,r分别属于哪个块
if(lk==rk)
{
for(rint i=l;i<=r;i++) a[i]+=v;//如果在一个块内直接暴力加，时间复杂度一样是 sqrt(n)
}
else
{
for(rint i=lk+1;i<rk;i++) add[i]+=v;//先加整块
for(rint i=l;i<=ed[lk];i++) a[i]+=v;//左右两边的散块都要加
for(rint i=r;i>=st[rk];i--) a[i]+=v;
}
}
inline int query(rint x)
{
return a[x]+add[pos[x]];
}
signed main()
{
rint n=_,b=sqrt(n);
for(rint i=1;i<=n;i++) a[i]=_;
rint t=n/b;
if(n%b) t++;//不整除再单独分一个块
for(rint i=1;i<=t;i++)//记录每个块的开始与结尾
{
st[i]=ed[i-1]+1;
ed[i]=st[i]+b-1;
}
ed[t]=n;//最后一个块结尾必然是n
for(rint i=1;i<=n;i++)//记录每个下标是哪个块
{
pos[i]=(i+b-1)/b;
}
for(rint i=1;i<=n;i++)
{
rint op=_,l=_,r=_,c=_;
if(!op)
{
modify(l,r,c);
}
else
{
out(query(r));
pc('\n');
}
}
return 0;
}
:::
P13979 数列分块入门 4
来看看这题，注意到相比与上题，这题之多了一个区间查询，怎么办呢？还是按照分块的思想区间查询的时候先把大块加上，然后暴力加上散块，查询时间复杂度 \(\mathcal{O}(\sqrt n)\)。
但是我们需要设置两个数组，一个存块中每个元素的增加量，一个是整个块的初始值与散块加的量。
:::success[Ac Code]
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define _ read<int>()
#define R register
#define rint register int
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=3e5+10,B=550;
int a[N],add[B],pos[N],st[B],ed[N],b,sum[B];
inline void modify(rint l,rint r,rint v)
{
rint lp=pos[l],rp=pos[r];
if(lp==rp)
{
for(rint i=l;i<=r;++i) a[i]+=v; sum[lp]+=(r-l+1)*v;
}
else
{
for(rint i=lp+1;i<rp;++i) add[i]+=v;
for(rint i=l;i<=ed[lp];++i) a[i]+=v;
sum[lp]+=(ed[lp]-l+1)*v;
for(rint i=st[rp];i<=r;++i) a[i]+=v;
sum[rp]+=(r-st[rp]+1)*v;
}
}
inline int query(rint l,rint r)
{
rint lp=pos[l],rp=pos[r],ans=0;
if(lp==rp)
{
for(rint i=l;i<=r;++i) ans+=a[i]+add[lp];
}
else
{
for(rint i=lp+1;i<rp;++i) ans+=add[i]*(ed[i]-st[i]+1)+sum[i];
for(rint i=l;i<=ed[lp];++i) ans+=a[i]+add[lp];
for(rint i=st[rp];i<=r;++i) ans+=a[i]+add[rp];
}
return ans;
}
signed main()
{
rint n=_;
for(rint i=1;i<=n;++i) a[i]=_;
b=sqrt(n);
rint t=n/b+(n%b?1:0);
for(rint i=1;i<=t;++i)
{
st[i]=ed[i-1]+1;
ed[i]=st[i]+b-1;
}
ed[t]=n;
for(rint i=1;i<=n;++i)
{
pos[i]=(i+b-1)/b;sum[pos[i]]+=a[i];
}
for(rint i=1;i<=n;++i)
{
rint op=_,l=_,r=_,c=_;
if(!op)
{
modify(l,r,c);
}
else
{
++c;out((query(l,r)%c+c)%c);pc('\n');
}
}
return 0;
}
:::
P13983 数列分块入门 8
题意很简单，不过多赘述了。
对于散块我们直接暴力查询并修改。但是对于整块，你发现不好去直接修改，怎么办呢？我们考虑对每个整块设置一个标记，当标记为真时，我们就将整个块都重置？错！显然这与 \(\mathcal{O}(n^2)\) 无异，所以我们考虑每次遇到散块，或者未被标记的整块暴力重置，我猜你想问：那这样时间复杂度也会超的吧？
首先，对于散块，是 \(\mathcal{O}(\sqrt n)\) 这个毋庸置疑，对于整块，你发现序列中一共 \(\frac{n}{b}\)（\(b\) 为块长）个整块，只要被操作过，必然会被重置，也就是说每个块最多在第一次重置时需要 \(\mathcal{O}(\sqrt n)\) 的复杂度，其余都是 \(\mathcal{O}(1)\)。
对于整块我们考虑打上一个标记，每次修改的时候先把标记下放，然后再操作。
:::success[Ac Code]
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define _ read<int>()
#define R register
#define rint register int
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=3e5+10,B=911;
int a[N],st[B],ed[B],setx[B],pos[N];
bitset<B>setc;
inline int query(rint l,rint r,rint c)
{
rint lp=pos[l],rp=pos[r],ans=0;
if(lp==rp)
{
if(setc[lp])for(rint i=st[lp];i<=ed[lp];++i) a[i]=setx[lp];setc[lp]=0;
for(rint i=l;i<=r;++i)
{
ans+=(a[i]==c);
}
}
else
{
if(setc[lp]) for(rint i=st[lp];i<=ed[lp];++i) a[i]=setx[lp];setc[lp]=0;
if(setc[rp]) for(rint i=st[rp];i<=ed[rp];++i) a[i]=setx[rp];setc[rp]=0;
for(rint i=l;i<=ed[lp];++i) ans+=(a[i]==c);
for(rint i=st[rp];i<=r;++i) ans+=(a[i]==c);
for(rint i=lp+1;i<rp;++i)
{
if(setc[i]) ans+=(setx[i]==c?ed[i]-st[i]+1:0);
else
{
for(rint j=st[i];j<=ed[i];++j) ans+=(a[j]==c);
}
}
}
return ans;
}
inline void modify(rint l,rint r,rint c)
{
rint lp=pos[l],rp=pos[r];
if(lp==rp)
{
if(setc[lp]&&setx[lp]==c) return;
if(setc[lp]) for(rint i=st[lp];i<=ed[lp];++i) a[i]=setx[lp];setc[lp]=0;
for(rint i=l;i<=r;++i) a[i]=c;
}
else
{
if(!setc[lp]||setx[lp]!=c)
{
if(setc[lp])
{
for(rint i=st[lp];i<=ed[lp];++i) a[i]=setx[lp];
setc[lp]=0;
}
for(rint i=l;i<=ed[lp];++i) a[i]=c;
}
if(!setc[rp]||setx[rp]!=c)
{
if(setc[rp])
{
for(rint i=st[rp];i<=ed[rp];++i) a[i]=setx[rp];
setc[rp]=0;
}
for(rint i=st[rp];i<=r;++i) a[i]=c;
}
for(rint i=lp+1;i<rp;++i)
{
setc[i]=1,setx[i]=c;
}
}
}
signed main()
{
rint n=_;
for(rint i=1;i<=n;++i) a[i]=_;
rint b=sqrt(n),t=n/b;
if(n%b)++t;
for(rint i=1;i<=t;++i)
{
st[i]=ed[i-1]+1;
ed[i]=st[i]+b-1;
}
for(rint i=1;i<=n;++i) pos[i]=(i+b-1)/b;
for(rint i=1;i<=n;++i)
{
rint l=_,r=_,c=_;
out(query(l,r,c));
pc('\n');modify(l,r,c);
}
return 0;
}
:::
P13982 数列分块入门 7
显然，题目要求区间修改单点查询比线段树 2 好点，由于优先级问题，我们按照线段数的懒标记思想，每当我们进行乘或加修改时，先把散块的乘 / 加标记清空，然后再懒标记。
我们定义 \(mul_i\) 为第 \(i\) 个块需要乘的数，\(add_i\) 则为第 \(i\) 个块需要加的数。
考虑对于散块的懒标记下放，注意到修改肯定形如：+……+*……*+……+*……*+……+*……* 这样的修改，也就是说，当我们某次乘法修改，前一次的修改为加法修改时，此时的乘法标记必然为 \(1\)，同样的，当我们在进行第一次加法修改时，且前一个修改为乘法标记，那么此时的加法标记必然为 \(0\)，因为我们每次加/乘修改都会将乘/加标记清除。
为了方便，我们将下方给下标为 \(i\) 的值下放的表达式为：\(a_i=a_i mul_{pos_i}+add_{pos_i}\)。
:::success[Ac Code]
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define _ read<int>()
#define R register
#define rint register int
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=3e5+10,B=550,P=10007;
int a[N],add[B],pos[N],st[B],ed[N],b,mul[B];
inline void modify(rint l,rint r,rint v)
{
rint lp=pos[l],rp=pos[r];
if(lp==rp)
{
for(rint i=st[lp];i<=ed[lp];++i) a[i]=((a[i]*mul[lp])%P+add[lp])%P;
mul[lp]=1,add[lp]=0;
for(rint i=l;i<=r;++i) a[i]=(a[i]+v)%P;
}
else
{
for(rint i=lp+1;i<rp;++i) add[i]=(add[i]+v)%P;
for(rint i=st[lp];i<=ed[lp];++i) a[i]=((a[i]*mul[lp])%P+add[lp])%P;mul[lp]=1,add[lp]=0;
for(rint i=l;i<=ed[lp];++i) a[i]=(a[i]+v)%P;
for(rint i=st[rp];i<=ed[rp];++i) a[i]=((a[i]*mul[rp])%P+add[rp])%P;mul[rp]=1,add[rp]=0;
for(rint i=st[rp];i<=r;++i) a[i]=(a[i]+v)%P;
}
}
inline void modify1(rint l,rint r,rint v)
{
rint lp=pos[l],rp=pos[r];
if(lp==rp)
{
for(rint i=st[lp];i<=ed[lp];++i) a[i]=((a[i]*mul[lp])%P+add[lp])%P;
mul[lp]=1,add[lp]=0;
for(rint i=l;i<=r;++i) a[i]=(a[i]*v)%P;
}
else
{
for(rint i=lp+1;i<rp;++i) mul[i]=(mul[i]*v)%P,add[i]=(add[i]*v)%P;
for(rint i=st[lp];i<=ed[lp];++i) a[i]=((a[i]*mul[lp])%P+add[lp])%P;mul[lp]=1,add[lp]=0;
for(rint i=l;i<=ed[lp];++i) a[i]=(a[i]*v)%P;
for(rint i=st[rp];i<=ed[rp];++i) a[i]=((a[i]*mul[rp])%P+add[rp])%P;mul[rp]=1,add[rp]=0;
for(rint i=st[rp];i<=r;++i) a[i]=(a[i]*v)%P;
}
}
inline int query(rint x)
{
return (a[x]*mul[pos[x]]%P)+add[pos[x]]%P;
}
signed main()
{
rint n=_;
for(rint i=1;i<=n;++i) a[i]=_;
b=sqrt(n);
rint t=n/b+(n%b?1:0);
for(rint i=1;i<=t;++i)
{
st[i]=ed[i-1]+1;
ed[i]=st[i]+b-1;mul[i]=1;//注意乘法标记要初始化为1
}
ed[t]=n;
for(rint i=1;i<=n;++i)
{
pos[i]=(i+b-1)/b;
}
for(rint i=1;i<=n;++i)
{
rint op=_,l=_,r=_,c=_;
if(!op)
{
modify(l,r,c%P);
}
else if(op==1)
{
modify1(l,r,c%P);
}
else
{
++c;out((query(r)%P+P)%P);pc('\n');
}
}
return 0;
}
:::
P13981 数列分块入门 6
题解里一堆大神，不是 FHQ 就是块状链表，来看看分块如何做。
显然，普通分块是不好作的，我们考虑开 \(\sqrt n\) 个 vector 但最后也可能被插入到 \(n\)，于是我们考虑重构。
显然，每次插入后就重构是不优的，于是我们来考虑一下间隔多才重构。
显然，每次 vector 插入是 \(size(v)\) 的（\(size(v)\) 表示 vector 的长度）当 \(size(v)\) 的长度越来越大时，插入的时间复杂度也越来越多，注意到每次重构是 \(\mathcal{O}(n)\) 的，我选择间隔 \(10\sqrt n\) 来重构。
:::success[Ac Code]
#include<bits/stdc++.h>
using namespace std;
char buf[1<<20],*p1=buf,*p2=buf;
#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
#define pc putchar_unlocked
// #define int long long
#define R register
#define rint register int
#define _ read()
inline int read()
{
rint r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(long long x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=6e5+10;
vector<vector<int>>v;
int a[N];
inline auto find(rint p)
{
rint s=0;
for(rint i=0;i<v.size();++i)
{
if(s+v[i].size()<p) s+=v[i].size();
else return v[i].begin()+p-s-1;
}
return v.back().end();
}
inline int findk(rint p)
{
rint s=0;
for(rint i=0;i<v.size();++i)
{
if(s+v[i].size()<p) s+=v[i].size();
else return i;
}
return 0;
}
signed main()
{
rint n=_;
rint b=max(int(sqrt(n)),1);
v.resize(n/b+1);
rint cnt=0;
for(rint i=1;i<=n;++i)
{
v[i/b].push_back(_);
}
for(rint i=1;i<=n;++i)
{
rint op=_;
if(!op)
{
rint l=_,r=_;
v[findk(l)].emplace(find(l),r);++cnt;
if(cnt==10*b)
{
rint tmp=0;
for(rint j=0;j<v.size();++j)
{
for(rint x:v[j]) a[++tmp]=x;
}
b=max(int(sqrt(tmp)),1);v.clear();v.resize(tmp/b+5);
for(rint j=1;j<=tmp;++j)
{
v[j/b].emplace_back(a[j]);
}
cnt=0;
}
}
else
{
rint c=_;
out(*find(c));pc('\n');
}
}
return 0;
}
//我也要写吗
（请注意 \(a\) 要开到 \(6\times 10^5\)）
:::
P13977 数列分块入门 2
考虑二分。
我们考虑在建立一个个块的时候，对于每个块，都排序，于是我们就可以以多了只 \(\log\) 作为代价，快速统计查询，修改也是一样，用上标记，在二分的时候减去即可。
:::success[Ac Code]
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define _ read<int>()
#define R register
#define rint register int
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=3e5+10;
int a[N],pos[N],st[N],ed[N],n,b,t,d[N],add[N];
inline void init()
{
for(rint i=1;i<=n;i++) pos[i]=(i+b-1)/b;
memcpy(d,a,sizeof(a));
for(rint i=1;i<=t;i++)
{
st[i]=ed[i-1]+1;
ed[i]=min(n,st[i]+b-1);
sort(d+st[i],d+ed[i]+1);
}
}
inline void modify(rint l,rint r,rint v)
{
rint lk=pos[l],rk=pos[r];
if(lk==rk)
{
for(rint i=l;i<=r;i++) a[i]+=v;
for(rint i=st[lk];i<=ed[lk];i++) d[i]=a[i];
sort(d+st[lk],d+ed[lk]+1);
}
else
{
for(rint i=lk+1;i<rk;i++) add[i]+=v;
for(rint i=l;i<=ed[lk];i++) a[i]+=v;
for(rint i=st[lk];i<=ed[lk];i++) d[i]=a[i];
sort(d+st[lk],d+ed[lk]+1);
for(rint i=r;i>=st[rk];i--) a[i]+=v;
for(rint i=st[rk];i<=ed[rk];i++) d[i]=a[i];
sort(d+st[rk],d+ed[rk]+1);
}
}
inline int query(rint l,rint r,rint c)
{
rint ans=0,lk=pos[l],rk=pos[r];
if(lk==rk)
{
for(rint i=l;i<=r;i++)
{
if(a[i]+add[pos[i]]<c) ans++;
}
}
else
{
for(rint i=lk+1;i<rk;i++)
{
rint p=lower_bound(d+st[i],d+ed[i]+1,c-add[i])-d-st[i];
ans+=max(p,0ll);
}
for(rint i=l;i<=ed[lk];i++) if(a[i]+add[pos[i]]<c) ans++;
for(rint i=r;i>=st[rk];i--) if(a[i]+add[pos[i]]<c) ans++;
}
return ans;
}
signed main()
{
n=_,b=sqrt(n);
t=n/b+(n%b?1:0);
for(rint i=1;i<=n;i++)
{
a[i]=_;
}
init();
for(rint i=1;i<=n;i++)
{
rint op=_,l=_,r=_,c=_;
if(!op) modify(l,r,c);
else
{
out(query(l,r,c*c));
pc('\n');
}
}
return 0;
}
:::
P13978 数列分块入门 3
容易发现此题与上题一样，可以二分。
:::success[Ac Code]
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define _ read<int>()
#define R register
#define rint register int
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=3e5+10;
int a[N],pos[N],st[N],ed[N],n,b,t,d[N],add[N];
inline void init()
{
for(rint i=1;i<=n;i++) pos[i]=(i+b-1)/b;
memcpy(d,a,sizeof(int)*(n+1));
for(rint i=1;i<=t;i++)
{
st[i]=ed[i-1]+1;
ed[i]=min(n,st[i]+b-1);
sort(d+st[i],d+ed[i]+1);
}
}
inline void modify(rint l,rint r,rint v)
{
rint lk=pos[l],rk=pos[r];
if(lk==rk)
{
for(rint i=l;i<=r;i++) a[i]+=v;
for(rint i=st[lk];i<=ed[lk];i++) d[i]=a[i];
sort(d+st[lk],d+ed[lk]+1);
}
else
{
for(rint i=lk+1;i<rk;i++) add[i]+=v;
for(rint i=l;i<=ed[lk];i++) a[i]+=v;
for(rint i=st[lk];i<=ed[lk];i++) d[i]=a[i];
sort(d+st[lk],d+ed[lk]+1);
for(rint i=r;i>=st[rk];i--) a[i]+=v;
for(rint i=st[rk];i<=ed[rk];i++) d[i]=a[i];
sort(d+st[rk],d+ed[rk]+1);
}
}
inline int query(rint l,rint r,rint c)
{
rint ans=-1145141919810,lk=pos[l],rk=pos[r];
if(lk==rk)
{
for(rint i=l;i<=r;i++)
{
if(a[i]+add[pos[i]]<c) ans=max(ans,a[i]+add[pos[i]]);
}
}
else
{
for(rint i=lk+1;i<rk;i++)
{
rint p=lower_bound(d+st[i],d+ed[i]+1,c-add[i])-d-1;
if(p>=st[i]&&d[p]+add[i]<c) ans=max(d[p]+add[i],ans);
}
for(rint i=l;i<=ed[lk];i++) if(a[i]+add[pos[i]]<c) ans=max(ans,a[i]+add[pos[i]]);
for(rint i=r;i>=st[rk];i--) if(a[i]+add[pos[i]]<c) ans=max(ans,a[i]+add[pos[i]]);
}
return ans==-1145141919810?-1:ans;
}
signed main()
{
n=_,b=sqrt(n);
t=n/b+(n%b?1:0);
for(rint i=1;i<=n;i++)
{
a[i]=_;
}
init();
for(rint i=1;i<=n;i++)
{
rint op=_,l=_,r=_,c=_;
if(!op) modify(l,r,c);
else
{
out(query(l,r,c));
pc('\n');
}
}
return 0;
}
:::
P13980 数列分块入门 5
其实你自己试试就会发现，对于一个数它一直根号下去是很快就会到 \(1\) 的，其实网上有证明，如果向下取整大约 \(\log \log x\) 就会到 \(1\)。
于是我们记录每个块的最大值，只要最大值为 \(1\) 就不修改。
时间复杂度 \(\Theta(n \sqrt n \log \log V)\)。
:::success[Ac Code]
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define rint register int
#define R register
#define _ read<int>()
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=3e5+10,B=1000,INF=1145141919810;
int a[N],pos[N],st[B],ed[B],add[B],maxx[B],sum[B];
inline void modify(rint l,rint r)
{
rint lp=pos[l],rp=pos[r];
if(lp==rp)
{
for(rint i=l;i<=r;++i) a[i]=sqrt(a[i]);
maxx[lp]=-INF,sum[lp]=0;
for(rint i=st[lp];i<=ed[rp];++i) maxx[lp]=max(maxx[lp],a[i]),sum[lp]+=a[i];
}
else
{
for(rint i=lp+1;i<rp;++i)
{
if(maxx[i]<=1) continue;
maxx[i]=-INF,sum[i]=0;
for(rint j=st[i];j<=ed[i];++j) a[j]=sqrt(a[j]),maxx[i]=max(maxx[i],a[j]),sum[i]+=a[j];
}
for(rint i=l;i<=ed[lp];++i) a[i]=sqrt(a[i]);
maxx[lp]=-INF,sum[lp]=0;
for(rint i=st[lp];i<=ed[lp];++i) maxx[lp]=max(maxx[lp],a[i]),sum[lp]+=a[i];
for(rint i=st[rp];i<=r;++i) a[i]=sqrt(a[i]);
maxx[rp]=-INF,sum[rp]=0;
for(rint i=st[rp];i<=ed[rp];++i) maxx[rp]=max(maxx[rp],a[i]),sum[rp]+=a[i];
}
}
inline int query(rint l,rint r)
{
rint lp=pos[l],rp=pos[r],ans=0;
if(lp==rp)
{
for(rint i=l;i<=r;++i) ans+=a[i];
}
else
{
for(rint i=l;i<=ed[lp];++i) ans+=a[i];
for(rint i=lp+1;i<rp;++i) ans+=sum[i];
for(rint i=st[rp];i<=r;++i) ans+=a[i];
}
return ans;
}
signed main()
{
rint n=_;
for(rint i=1;i<=n;++i) a[i]=_;
memset(maxx,-0x3f,sizeof(maxx));
rint b=sqrt(n),t=n/b+(n%b?1:0);
for(rint i=1;i<=t;++i)
{
st[i]=ed[i-1]+1;
ed[i]=min(st[i]+b-1,n);
}
for(rint i=1;i<=n;++i)
{
pos[i]=(i+b-1)/b;
maxx[pos[i]]=max(maxx[pos[i]],a[i]);
sum[pos[i]]+=a[i];
}
for(rint i=1;i<=n;++i)
{
rint op=_,l=_,r=_;
if(!op) modify(l,r);
else
{
out(query(l,r));pc('\n');
}
}
return 0;
}
:::
P13984 数列分块入门 9
紫色欸。
本题不要求在线，事实上回滚莫队也可以解决此题（而且常数小），回滚莫队在下文会讲解，在这先介绍分块做法。
考虑记录 \(s_{i,j}\) 为元素 \(j\) 在 \(1\dots j\) 块出现了多少次，类似于前缀和。
记 \(p_{i,j}\) 为 \(i\dots j\) 块中的众数是谁，出现了多少次。
显然，因为值域太大，需要离散化。
考虑如何预处理出 \(s_{i,j}\) 与 \(p_{i,j}\)。\(s_{i,j}\) 直接枚举每个块，然后对于每个做类似于前缀和的预处理即可，时间复杂度 \(\mathcal{O}(n\sqrt n)\)，\(p_{i,j}\) 直接暴力枚举块，然后遍历，时间复杂度：\(\mathcal{O}(\sqrt n \sqrt n \sqrt n=n\sqrt n)\)。
处理出两个数组后，查询就很简单了，直接处理就好了。（有点卡常）
:::success[Ac Code]
#include<bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
// #define int long long
#define R register
#define rint register int
#define _ read<int>()
inline bool blank(const char x)
{
return !(x^9)||!(x^13)||!(x^10)||!(x^32);
}
template<class T>inline T read()
{
T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(int x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
inline void read(char &x)
{
for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=3e5+10,B=600;
int a[N],pos[N],st[N],ed[N],s[B][N],c[N];
pair<int,int>p[B][B];
vector<int>tmp;
signed main()
{
rint n=_;rint q=n;
for(rint i=1;i<=n;++i) a[i]=_;
tmp.assign(a+1,a+n+1);
sort(tmp.begin(),tmp.end());
tmp.erase(unique(tmp.begin(),tmp.end()),tmp.end());
for(rint i=1;i<=n;++i)
{
a[i]=lower_bound(tmp.begin(),tmp.end(),a[i])-tmp.begin();
}
rint b=sqrt(n)+3,t=n/b;
if(n%b) ++t;
for(rint i=1;i<=t;++i) st[i]=ed[i-1]+1,ed[i]=st[i]+b-1;
for(rint i=1;i<=n;++i) pos[i]=(i+b-1)/b;
for(rint i=1;i<=t;++i)
{
for(rint v=0;v<tmp.size();++v) s[i][v]=s[i-1][v];
for(rint j=st[i];j<=ed[i];++j) ++s[i][a[j]];
}
for(rint i=1;i<=t;++i)
{
pair<int,int>tm=make_pair(0,0);
for(rint j=i;j<=t;++j)
{
for(rint k=st[j];k<=ed[j];++k)
{
if(tm.second<++c[a[k]]||(tm.second==c[a[k]]&&tm.first>a[k])) tm={a[k],c[a[k]]};
}
p[i][j]=tm;
}
memset(c,0,tmp.size()*sizeof(int));
}
rint l,r,lp,rp,maxx,ans,jc;
while(q--)
{
l=_,r=_,lp=pos[l],rp=pos[r],maxx=0,ans;
if(rp-lp<=1)
{
for(rint i=l;i<=r;++i)
{
if(maxx<++c[a[i]]||(maxx==c[a[i]]&&ans>a[i])) maxx=c[a[i]],ans=a[i];
}
}
else
{
maxx=p[lp+1][rp-1].second,ans=p[lp+1][rp-1].first;
for(rint i=l;i<=ed[lp];++i)
{
jc=s[rp-1][a[i]]-s[lp][a[i]];
if(maxx<++c[a[i]]+jc||(maxx==c[a[i]]+jc&&ans>a[i])) maxx=c[a[i]]+jc,ans=a[i];
}
for(rint i=st[rp];i<=r;++i)
{
jc=s[rp-1][a[i]]-s[lp][a[i]];
if(maxx<++c[a[i]]+jc||(maxx==c[a[i]]+jc&&ans>a[i])) maxx=c[a[i]]+jc,ans=a[i];
}
}
memset(c,0,tmp.size()*sizeof(int));
out(tmp[ans]);pc('\n');
}
return 0;
}
//我也要写吗
:::
总结
什么时候使用分块？当数据范围可以接受 \(\mathcal{O}(n\sqrt n)\) 的时候，你就可以
莫队
0. 前言
莫队是由莫涛提出的算法，是一种非常好用的离线算法，在莫队上加以改进还能支持树上问题与修改。
1. 普通莫队
P3901 数列找不同
这个可以使用树状数组和线段树解决，但是今天我们不讲这两种做法，我们看看莫队怎么做。
首先暴力，对于每次查询时间复杂度最坏是 \(\mathcal{O}(n)\)，那么我们考虑一下优化，我们发现每次都重新枚举区间实际上非常耗时间，于是我们考虑不重置指针，让它慢慢往询问移动，这就是莫队，一般来说移动时间复杂度是 \(\mathcal{O}(1)\) 的，就可以使用莫队来解决。
但是我们发现，如果你每一次询问的区间间隔都很远的话那时间复杂度最坏还是 \(\mathcal{O}(nq)\)，那我们考虑将这些询问排序这样就不用每次都移动的很远。
那么我们该怎么排序呢，事实上莫队并没有最优的排序方法，不过我们通常采用分块的思想，就是把一个序列分成很多块然后按照询问的左端点所在的块的序号从小到大排序，如果相等那就按照右端点从小到大排，为什么可以呢？我举个例子。
比如现在有个图书馆然后管理员要去每个书架上拿书：
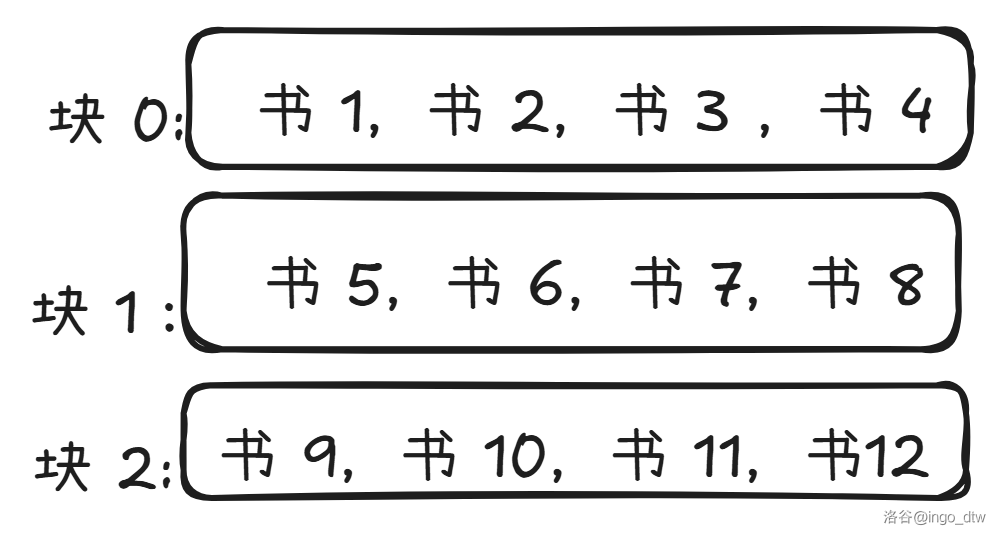那你现在是管理员你该怎么去拿？肯定是按照块的序号吧，不然移动次数会变多，然后为什么再按照右端点从小到大排呢？因为按顺序嘛，否则你现在在 \(13\) 等会要去 \(9\) 又要去 \(11\) 这重复移动的次数不就更多了吗？示例代码：
sort(qry+1,qry+q+1,cmp);//排序
int l=1,r=0;
for(int i=1;i<=q;i++)//处理每个询问
{
if(l>qry[i].l) add(a[--l]);//左端点大于这个询问
if(l<qry[i].l) del(a[l++]);//左端点小于这个询问
if(r<qry[i].r) add(a[++r]);//右端点小于这个询问
if(r>qry[i].r) del(a[r++]);//右端点大于这个询问
}
现在我们讨论一下块的大小怎么定，首先我们看到上面的代码，我们来分析一下左指针 \(l\)，和右指针 \(r\) 的移动次数：
if(l>qry[i].l) add(a[--l]);//左端点大于这个询问
if(l<qry[i].l) del(a[l++]);//左端点小于这个询问
对于这个左端点最多移动次数为 \(b\)（块长），总移动次数为 \(q\times b\)。
if(r<qry[i].r) add(a[++r]);//右端点小于这个询问
if(r>qry[i].r) del(a[r++]);//右端点大于这个询问
每个块的右指针最多移动 \(n\) 次，有 \(\frac{n}{b}\) 个块，所以总移动次数为 \(n^2\div b\)。
你发现如果块长比较小，那么 \(l\) 指针的移动次数就小，但是 \(r\) 指针的移动次数又增大了，反之如果块长比较大，那么 \(l\) 指针的移动次数就大，但是 \(r\) 又减小了。
那么总时间复杂度为 \(\mathcal{O}(T(b))\)，\(T(b)=qb+\frac{n^2}{b}\)（\(b\) 为块长，且 \(b>0\)），我们现在感性的理解一下发现 \(b=\sqrt{n}\) 时时间复杂度为 \(\mathcal{O}(n\sqrt{n})\)。
:::info[详细证明]
令：
\[x = qb, \quad y = \frac{n^2}{b}
\]
应用二元均值不等式：
\[x + y \geq 2\sqrt{xy}
\]
代入：
\[qb + \frac{n^2}{b} \geq 2\sqrt{qb \times \frac{n^2}{b}} = 2\sqrt{qn^2} = 2n\sqrt{q}
\]
均值不等式取等号当且仅当：
\[x = y \quad \Rightarrow \quad qb = \frac{n^2}{b}
\]
解这个方程：
\[qb = \frac{n^2}{b} \Rightarrow qb^2 = n^2 \Rightarrow b^2 = \frac{n^2}{q} \Rightarrow b = \frac{n}{\sqrt{q}}
\]
当 \(b = \frac{n}{\sqrt{q}}\) 时：
\[T(b) = q \times \frac{n}{\sqrt{q}} + \frac{n^2}{n/\sqrt{q}} = n\sqrt{q} + n\sqrt{q} = 2n\sqrt{q}
\]
这是理论上的最小成本。
特别的：当 \(n \approx q\) 时：
\[b = \frac{n}{\sqrt{q}} \approx \frac{n}{\sqrt{n}} = \sqrt{n}
\]
:::
所以对于上面的题目，我们考虑维护一个变量，还有一个桶：
- 在
add时，如果加上这个数，这个数出现的次数等于 \(2\)，那么 \(tmp+1\)。 - 在
del时，如果减去这个数，这个数的出现次数等于 \(1\)，那么 \(tmp-1\)。 - 答案数组记录 \(tmp\) 是否为 \(0\)，如果为 \(0\) 输出
No，否则输出Yes。
为什么要维护一个 int？因为如果维护一个 bool 那么在 del 时可能有多个重复，但是一归 \(0\) 就全都不算了，所以需要维护变量。
:::success[Ac Code]
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define R register
#define _ read<int>()
// #define int long long
#define rint register int
inline bool blank(const char &x)
{
return !(x ^ 32) || !(x ^ 10) || !(x ^ 13) || !(x ^ 9);
}
template<class T> inline T read()
{
T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f * r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=1e5+10;
bitset<N>ans;
struct oi
{
int l,r,id;
}qry[N];
int a[N],b,mp[N],tmp=0;
inline bool cmp(const oi &x,const oi &y)
{
if(x.l/b!=y.l/b) return x.l/b<y.l/b;
return x.r<y.r;
}
inline void add(rint x)
{
mp[x]++;
if(mp[x]==2) tmp++;
}
inline void del(rint x)
{
mp[x]--;
if(mp[x]==1) tmp--;
}
signed main()
{
rint n=_,q=_;
b=sqrt(n);
for(rint i=1;i<=n;i++) a[i]=_;
for(rint i=1;i<=q;i++)
{
qry[i].l=_,qry[i].r=_,qry[i].id=i;
}
sort(qry+1,qry+q+1,cmp);
rint l=1,r=0;
for(rint i=1;i<=q;i++)
{
while(l<qry[i].l) del(a[l++]);
while(l>qry[i].l) add(a[--l]);
while(r>qry[i].r) del(a[r--]);
while(r<qry[i].r) add(a[++r]);
if(tmp) ans[qry[i].id]=1;
else ans[qry[i].id]=0;
}
for(rint i=1;i<=q;i++)
{
if(!ans[i]) puts("Yes");
else puts("No");
}
return 0;
}
:::
P2709 小 B 的询问 /【模板】莫队
这个甚至比上面的还简单，只需维护一个数出现了几次，然后按照题目要求计算答案即可，于是你一交就 T 了，我们发现 \(\mathcal{O}(kn\sqrt{n})\approx 25\times 10^8\times 2\times 10^2\approx2.5\times10^{11}\) 显然不可以过（虽然常数小就过去了），我们发现没必要每次询问都将答案从新计算，我们将式子拆一下那么（\(mp_x\) 为 \(x\) 的出现次数）：
del对答案的影响为 \(-(2\times mp_x+1)\)。add对答案的影响为 \(+(2\times mp_x+1)\)。
:::success[Ac Code]
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define R register
#define _ read<int>()
// #define int long long
#define rint register int
inline bool blank(const char &x)
{
return !(x ^ 32) || !(x ^ 10) || !(x ^ 13) || !(x ^ 9);
}
template<class T> inline T read()
{
T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f * r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=1e5+10;
int ans[N];
struct oi
{
int l,r,id;
}qry[N];
int a[N],b,mp[N],tmp=0;
inline bool cmp(const oi &x,const oi &y)
{
if(x.l/b!=y.l/b) return x.l/b<y.l/b;
return x.r<y.r;
}
inline void add(rint x)
{
tmp+=(mp[x]<<1)+1;
mp[x]++;
}
inline void del(rint x)
{
tmp-=(mp[x]<<1)-1;
mp[x]--;
}
signed main()
{
rint n=_,q=_,k=_;
b=sqrt(n);
for(rint i=1;i<=n;i++) a[i]=_;
for(rint i=1;i<=q;i++)
{
qry[i].l=_,qry[i].r=_,qry[i].id=i;
}
sort(qry+1,qry+q+1,cmp);
rint l=1,r=0;
for(rint i=1;i<=q;i++)
{
while(l<qry[i].l) del(a[l++]);
while(l>qry[i].l) add(a[--l]);
while(r>qry[i].r) del(a[r--]);
while(r<qry[i].r) add(a[++r]);
ans[qry[i].id]=tmp;
}
for(rint i=1;i<=q;i++)
{
out(ans[i]);
pc('\n');
}
return 0;
}
:::
2. 带修莫队
我们现在来看看带修莫队，问题就是在上面的基础上，还带一个修改，现在我们应该怎么做？
我们干脆直接再维护一个变量 \(t\)，我们就认为这个修改是根据时间来的，所以在莫队更新时再加一个 \(t\) 的，要把当前时间轴移动到询问的时间。
现在我们再考虑一个问题，那就是怎么排序呢？与普通莫队不同，带修莫队排序的第二关键字为 \(r\) 所在块的块长，第三关键字就是 \(t\) 的大小。
否则你换个顺序（\(t\) 为第一关键字，或者 \(r\) 为第一关键字）不管怎么换都是会超时，如果读者感兴趣可以自己手动模拟一下。
块长一般取 \(n^{\frac{2}{3}}\)（感兴趣的读者可以自行推导，这里不过多赘述 因为我不会）
P1903 [国家集训队] 数颜色 / 维护队列 /【模板】带修莫队
:::success[Ac Code]
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define R register
#define _ read<int>()
// #define int long long
#define rint register int
inline bool blank(const char &x)
{
return !(x^13)||!(x^9)||!(x^32)||!(x^10);
}
template<class T> inline T read()
{
T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f * r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
inline void read(char &x)
{
for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=1e6+10;
int ans[N];
struct oi
{
int l,r,id,t;
}qry[N],qq[N];
int a[N],b,mp[N],tmp=0,cnt,cntt;
inline bool cmp(const oi &x,const oi &y)
{
if(x.l/b!=y.l/b) return x.l<y.l;
if(x.r/b!=y.r/b) return x.r<y.r;
return x.t<y.t;
}
inline void add(rint x)
{
mp[x]++;
if(mp[x]==1) tmp++;
}
inline void del(rint x)
{
mp[x]--;
if(!mp[x]) tmp--;
}
inline void upd(rint x,rint t)
{
if(qry[x].l<=qq[t].l&&qq[t].l<=qry[x].r)
{
del(a[qq[t].l]);
add(qq[t].r);
}
swap(a[qq[t].l],qq[t].r);//下一次肯定相反所以直接交换位置没必要再写一个
}
signed main()
{
rint n=_,q=_;
b=pow(n,2.0/3.0);
for(rint i=1;i<=n;i++) a[i]=_;
cnt=0;
for(rint i=1;i<=q;i++)
{
char x;
read(x);
if(x=='Q') qry[++cnt]={_,_,cnt,cntt};//注意这里是cnt不是i
else qq[++cntt]={_,_,0,0};
}
sort(qry+1,qry+cnt+1,cmp);
rint l=1,r=0,t=0;
for(rint i=1;i<=cnt;i++)
{
while(l<qry[i].l) del(a[l++]);
while(l>qry[i].l) add(a[--l]);
while(r>qry[i].r) del(a[r--]);
while(r<qry[i].r) add(a[++r]);
while(t>qry[i].t) upd(i,t--);//修改时间
while(t<qry[i].t) upd(i,++t);
ans[qry[i].id]=tmp;
}
for(rint i=1;i<=cnt;i++)
{
out(ans[i]);
pc('\n');
}
return 0;
}
注意一下，\(t\) 的移动是 \(l\) 和 \(r\) 移动之后，因为在这之前这个询问的答案还没更新。
:::
3. 回滚莫队
当 del 函数或 add 函数不好实现时，我们干脆之使用可以实现的函数，剩下的交给回滚解决，因为只删除莫队与只添加莫队并无很大区别，故在这里只展示只添加莫队。
P14420 [JOISC 2014] 历史的研究 / Historical Research
来看道例题，注意到这个题的撤销操作不好实现，因为你不好找到第二大的值，故我们使用只添加莫队。
其他的操作和普通莫队一样，但是我们需要记住，既然删除操作不好作，那么我们就只增加，剩下的交给回滚来解决。
首先我们先离散化，然后我们排序时不可进行奇偶性优化，这样可以保证按顺序处理询问时右端点单调不减。
注意到因为我们的排序列，右端点单调不减，但是左端点万一要加呢？聪明的你肯定想到，我们开始直接把左端点给设置为这个块的右端点，这样就可以报持左端点单不升。
可是你又注意到如过我们保持上一次操作完的左端点，这个时候如果我们现在的左端点要大于上一次的，我们又需要增加左端点了，这个时候回滚的作用就出来了，既然我们想让左端点不增，那么当我们处理新的左指针与上次不在一个块那么就将左指针初始设为这个块的右端点，这样可以保持左指针单调不增。
具体的，我们先处理右指针小于的情况，把答案和当前的左指针记录下来，然后我们再把左指针向左移动，处理出当前询问的答案后，我们再将左指针回退到我们处理完右端点后的情况，而这个重置了后的左指针的答案我们已经记录了，无需再求，只需将回退的这段区间的所有元素出现次数减掉就好。
还有个需要特判的情况，当这次询问的左右端点在一个块内，我们可以直接暴力求出答案，时间复杂度也是 \(\mathcal{O}(\sqrt n)\)。
:::info[时间复杂度]
设 \(b\) 为块长，对于每次询问：
- 如果左端点和右端点在一个块，那么时间复杂度为 \(\mathcal{O}(b)\)
- 否则，我们考虑左端点都在一个块的询问，右指针单调递增所以移动复杂度为 \(\mathcal{O}(n)\)，左指针移动 \(\mathcal{O}(b)\)，有 \(\frac{n}{b}\) 个块，所以时间复杂度为 \(\mathcal{O}(\frac{n}{b}n+mb=\frac{n^2}{b}+mb)\) 当 \(b=\frac{n}{\sqrt m}\) 时最优，此时时间复杂度为 \(\mathcal{O}(2 n\sqrt m\approx n\sqrt m)\)。
:::
:::success[Ac Code]
#include<bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define R register
#define rint register int
#define _ read<int>()
inline bool blank(const char x)
{
return !(x^9)||!(x^13)||!(x^10)||!(x^32);
}
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(int x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
inline void read(char &x)
{
for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=1e5+10;
struct qry
{
int l,r,id;
}q[N];
int a[N],b,c[N],ans,anss[N];
vector<int>tmp;
inline bool cmp(const qry &x,const qry& y)
{
if(x.l/b==y.l/b) return x.r<y.r;
return x.l/b<y.l/b;
}
inline void add(rint x)
{
ans=max(ans,++c[x]*tmp[x]);
}
inline void del(rint x)
{
--c[x];
}
signed main()
{
rint n=_,m=_;
for(rint i=1;i<=n;++i) a[i]=_;
tmp.assign(a+1,a+n+1);
sort(tmp.begin(),tmp.end());
tmp.erase(unique(tmp.begin(),tmp.end()),tmp.end());
for(rint i=1;i<=n;++i) a[i]=lower_bound(tmp.begin(),tmp.end(),a[i])-tmp.begin();
for(rint i=1;i<=m;++i) q[i]={_,_,i};
b=sqrt(n);
sort(q+1,q+m+1,cmp);
rint l,r;l=1,r=0;
for(rint i=1;i<=m;++i)
{
if(i==1||q[i].l/b!=q[i-1].l/b)
{
for(rint j=l;j<=r;++j) del(a[j]);
l=(q[i].l/b+1)*b;//重置指针
r=l-1;
ans=0;
}
if(q[i].l/b==q[i].r/b)
{
for(rint j=q[i].l;j<=q[i].r;++j) add(a[j]);
anss[q[i].id]=ans;
for(rint j=q[i].r;j>=q[i].l;--j) del(a[j]);
ans=0;
}
else
{
while(r<q[i].r) add(a[++r]);
rint tans=ans,tl=l;
while(l>q[i].l) add(a[--l]);
anss[q[i].id]=ans;
while(tl>l) del(a[l++]);
ans=tans;
}
// cout<<q[i].id<<' '<<q[i].l<<' '<<q[i].r<<' '<<l<<' '<<r<<' '<<ans<<endl;
}
for(rint i=1;i<=m;++i)
{
out(anss[i]);pc('\n');
}
return 0;
}
//我也要写吗
:::
P5906 【模板】回滚莫队 & 不删除莫队
这题虽然是回滚莫队的模板题，但实际上我认为上一题更好作为模板题。
显然这个题的删除操作不好做，不太好知道怎么回退。（其实也可以用普通莫队，这个回退显然可以预处理位置）
我们考虑使用回滚莫队，我们考虑记录每个数字的第一次出现位置，与最后一次出现位置，但是有个问题，当我们回滚的时候，不仅需要将答案回退，还需在前面复制左指针移动前的数组，然后移动后再复制回来，显然，此做法常数很大。
但是我们还可以再弄一个数组，表示向左移动时临时的记录位置的数组，当我们回退时直接将这个数组清空，则不需要再将之前的数组全部复制。
但是这么写，我们就需写两个 del 与 add（其中的 del 不是普通莫队的 del）当我们临时扩展左指针时，有两种情况：
- 如若答案的最后一次出现位置在大于在最开始的左指针，那么答案是当前大于左指针的位置与当前位置的差。
- 如若答案最后一次出现次数小于最开始的左指针，第一次出现位置与最后一次出现位置就在最开始左指针之前。
（还是理解不了可以看看代码）
:::success[Ac Code]
#include<bits/stdc++.h>
using namespace std;
char buf[1<<20],*p1=buf,*p2=buf;
#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
#define pc putchar_unlocked
// #define int long long
#define R register
#define rint register int
#define _ read()
inline int read()
{
rint r=0,f=1;R char c=gc();
while(!isdigit(c)) c=gc();
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return r;
}
inline void out(long long x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=2e5+10;
int a[N],b,anss[N],ans,n;
pair<int,int>cx[N],px[N];
struct qry
{
int l,r,id;
}q[N];
vector<int>tmp;
inline bool cmp(const qry &x,const qry &y)
{
if(x.l/b!=y.l/b) return x.l/b<y.l/b;
return x.r<y.r;
}
inline void addr(rint x)
{
cx[a[x]].first=min(cx[a[x]].first,x);
cx[a[x]].second=max(cx[a[x]].second,x);
ans=max(ans,cx[a[x]].second-cx[a[x]].first);
}
inline void addl(rint x)
{
px[a[x]].first=min(px[a[x]].first,x);
px[a[x]].second=max(px[a[x]].second,x);
ans=max(ans,max(px[a[x]].second-px[a[x]].first,cx[a[x]].second-px[a[x]].first));
}
inline void delr(rint x)
{
if(cx[a[x]].second==x) cx[a[x]].second=0;
if(cx[a[x]].first==x) cx[a[x]].first=1145141;
}
inline void dell(rint x)
{
px[a[x]].first=1145141,px[a[x]].second=0;
}
signed main()
{
n=_;
for(rint i=1;i<=n;++i) a[i]=_;
tmp.assign(a+1,a+n+1);
sort(tmp.begin(),tmp.end());
tmp.erase(unique(tmp.begin(),tmp.end()),tmp.end());
for(rint i=1;i<=n;++i) a[i]=lower_bound(tmp.begin(),tmp.end(),a[i])-tmp.begin();
for(rint i=0;i<tmp.size();++i) cx[i].first=1145141,px[i].first=1145141;
rint m=_;
b=max(int(n/sqrt(m)),1);
for(rint i=1;i<=m;++i) q[i]={_,_,i};
sort(q+1,q+m+1,cmp);
rint l=1,r=0;
for(rint i=1;i<=m;++i)
{
if(i==1||q[i-1].l/b!=q[i].l/b)
{
for(rint j=l;j<=r;++j) delr(j);
l=(q[i].l/b+1)*b+1,r=l-1,ans=0;
}
if(q[i].l/b==q[i].r/b)
{
for(rint j=q[i].l;j<=q[i].r;++j) addr(j);
anss[q[i].id]=ans;
for(rint j=q[i].l;j<=q[i].r;++j) delr(j);
ans=0;
}
else
{
while(r<q[i].r) addr(++r);
rint tans=ans,tl=l;
while(l>q[i].l) addl(--l);
anss[q[i].id]=ans;
while(l<tl) dell(l++);
ans=tans;
}
}
for(rint i=1;i<=m;++i)
{
out(anss[i]);pc('\n');
}
return 0;
}
//我也要写吗
:::
P13984 数列分块入门 9
熟悉吗？我们来看看回滚莫队如何做。
首先，此题的增加也是好做的，难点在于减少，和最开始的历史的研究其实没什么区别，直接统计即可。
:::success[Ac Code]
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define rint register int
#define R register
#define _ read<int>()
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=3e5+10;
int a[N],c[N],b,ans,anss[N],maxx;
struct qry
{
int l,r,id;
}q[N];
vector<int>tmp;
inline bool cmp(const qry &x,const qry&y)
{
if(x.l/b!=y.l/b) return x.l/b<y.l/b;
return x.r<y.r;
}
inline void del(rint x)
{
--c[x];
}
inline void add(rint x)
{
if(maxx<++c[x]||(maxx==c[x]&&tmp[x]<ans))
{
maxx=c[x];ans=tmp[x];
}
}
signed main()
{
rint n=_;
for(rint i=1;i<=n;++i) a[i]=_;
tmp.assign(a+1,a+n+1);
sort(tmp.begin(),tmp.end());
tmp.erase(unique(tmp.begin(),tmp.end()),tmp.end());
for(rint i=1;i<=n;++i) a[i]=lower_bound(tmp.begin(),tmp.end(),a[i])-tmp.begin();
for(rint i=1;i<=n;++i) q[i]={_,_,i};
b=sqrt(n);
sort(q+1,q+n+1,cmp);
rint l=1,r=0;
for(rint i=1;i<=n;++i)
{
if(i==1||q[i].l/b!=q[i-1].l/b)
{
for(rint j=l;j<=r;++j) del(a[j]);
l=(q[i].l/b+1)*b,r=l-1,ans=maxx=0;
}
if(q[i].l/b==q[i].r/b)
{
for(rint j=q[i].l;j<=q[i].r;++j) add(a[j]);
anss[q[i].id]=ans;
for(rint j=q[i].l;j<=q[i].r;++j) del(a[j]);ans=maxx=0;
}
else
{
while(r<q[i].r) add(a[++r]);
rint tans=ans,tl=l,tmaxx=maxx;
while(l>q[i].l) add(a[--l]);
anss[q[i].id]=ans;
while(l<tl) del(a[l++]);
ans=tans,maxx=tmaxx;
}
// cout<<q[i].l<<' '<<q[i].r<<' '<<q[i].id<<' '<<ans<<endl;
}
for(rint i=1;i<=n;++i)
{
out(anss[i]);pc('\n');
}
return 0;
}//我也要写吗
:::
根号分治
听着这么高级，实际就是把两个暴力给拼起来。
P3396 哈希冲突
来看看例题。
不难注意到此题的 A 询问当 \(x\) 越来越大时，单次查询的时间复杂度就越来越小，于是我们就可以考虑预处理 \(s_{i,j}\) 表示下标模 \(i\) 为 \(j\) 的和，而且我们只处理模 \(\sqrt n\) 以内的，然后你就发现如果我们需要修改，也只需要模 \(\sqrt n\) 以内的。
那么此时查询时间复杂度大约 \(\mathcal{O}(\sqrt n)\) 修改也是 \(\mathcal{O}(n)\) 总时间复杂度 \(\mathcal{O}(n\sqrt n)\)。
:::success[Ac Code]
#include<bits/stdc++.h>
using namespace std;
#define gc getchar_unlocked
#define pc putchar_unlocked
// #define int long long
#define R register
#define rint register int
#define _ read<int>()
inline bool blank(const char x)
{
return !(x^9)||!(x^13)||!(x^10)||!(x^32);
}
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(int x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
inline void read(char &x)
{
for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=15e4+10,B=390;
int s[B][B],a[N];
signed main()
{
rint n=_,q=_;
for(rint i=1;i<=n;++i) a[i]=_;
for(rint i=1;i*i<=n;++i)
{
for(rint j=1;j<=n;++j)
{
s[i][j%i]+=a[j];
}
}
while(q--)
{
char op;read(op);
if(op=='A')
{
rint x=_,y=_;
if(x*x<=n)
{
out(s[x][y]);pc('\n');
}
else
{
rint sum=0;
for(rint i=y;i<=n;i+=x)
{
sum+=a[i];
}
out(sum);pc('\n');
}
}
else
{
rint x=_,y=_;
for(rint i=1;i*i<=n;++i)
{
s[i][x%i]+=(y-a[x]);
}
a[x]=y;
}
}
return 0;
}
//我也要写吗
:::
CF797E Array Queries
我认为此题显然没有蓝。
考虑暴力容易发现，与上题一样，此题的每次查询是和 \(k\) 相关的，也容易发现，当 \(k\) 很大时时间复杂度较小，于是我们考虑预处理 \(\sqrt n\) 以内的 \(k\) 既记 \(s_{i,j}\) 为第 \(i\) 个数加 \(k\) 大于 \(n\) 的次数。
:::success[Ac Code]
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define _ read<int>()
#define R register
#define rint register int
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
const int N=1e5+10,B=317;
int s[N][B],a[N];
signed main()
{
rint n=_;
for(rint i=1;i<=n;++i) a[i]=_;
for(rint i=n;i;--i)
{
for(rint j=1;j*j<=n;++j)
{
if(a[i]+i+j>n) s[i][j]=1;
else s[i][j]=s[i+a[i]+j][j]+1;
}
}
rint q=_;
while(q--)
{
rint p=_,k=_;
if(k*k<=n) out(s[p][k]);
else
{
rint ans=0;
while(1)
{
if(a[p]+p+k>n) {out(ans+1);break;}
else p=a[p]+k+p,++ans;
}
}
pc('\n');
}
return 0;
}
:::
4. 结尾
什么时候使用分块/莫队/根号分治？当数据范围可以接受 \(\mathcal{O}(n\sqrt n)\) 的时候，你就可以使用，当然很多情况下线段树比分块更好，只不过一般的线段树的扩展性比分块低很多。
其实当你看到数据范围是 \(x\times 10^5\) 就得想想分块/莫队/根号分治了。
在考场上，如果可以同时使用分块/莫队，建议使用莫队，只要题目不是强制在线，莫队一般都可以胜任，因为莫队的扩展性基本上比分块好（毕竟是离线算法），而且莫队的常数很小，比如上面的数列分块入门 9 使用分块做法真的很卡常。
块长一般选多少？莫队/分块/根号分治一般选择 \(\sqrt n\)，带修莫队选择 \(n^\frac{2}{3}\)，当然在某些需要卡常的情况下也不一定，只不过一般都选择这些。
总结 & upd
2026/2/14：添加了对分块/莫队/根号分治的总结与使用经验，祝各位情人节快乐！
关于根号的算法大概就这些了。（当然还有些树上没讲到）
如果你还有疑问，或者文章有错误欢迎在私信中向我询问或修改，感谢各位！
也感谢能看到这的读者，毕竟这玩意确实很多。（也谢谢管理，您应该看的眼睛有点累了吧）
浙公网安备 33010602011771号