浅析 FHQ-Treap&Treap

前言

\(\texttt{Treap}\) 就是 \(\texttt{Tree}\)（树）加上 \(\texttt{Heap}\)（堆），所以 \(\texttt{Treap}\) 可翻译为“树堆”。

首先，\(\texttt{Treap}\) 是二叉搜索平衡树的一种，分无旋，和有旋，其中无旋的 \(\texttt{Treap}\) 是由范浩强引入的，所以又称 \(\texttt{FHQ-Treap}\)。

对于 \(\texttt{FHQ-Treap}\) 有些优点，比如它如果做区间操作的话，很简单，而且它如果需要可持久化的话，也很简单，而且由于无旋，个人认为比 \(\texttt{Treap}\) 要好理解。

二叉搜索树（BST）

学平衡树，你首先得明白二叉搜索树，就是如果这棵树是二叉搜索树，那么根节点的左子树里的节点全都比根节点要小，根节点的右子树也全都比根节点要大，且根节点的左右子树也是二叉搜索树，特别的空树是一颗二叉搜索树。

\(\texttt{FHQ-Treap}\)

\(\texttt{FHQ-Treap}\) 的操作主要有分裂（split）和合并（merge）。

分裂

split 主要是将一个 \(\texttt{Treap}\) 分裂成两个 \(\texttt{Treap}\)，其中 \(l\) 的节点全部小于 \(k\)，而 \(r\) 的值全部大于等于 \(k\)。

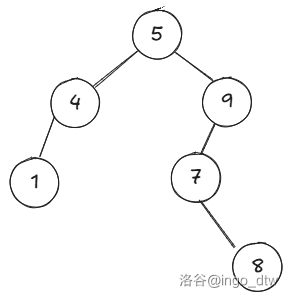
如上图，我们将 \(k=7\) 那么我们用非常若只的想法，一个个遍历然后按照规则丢就好了。

但是我们可以提升一下。不难发现上面那样做分裂是 \(\mathcal{O}(V)\)（\(V\) 是顶点数）的，但是因为 \(\texttt{FHQ-Treap}\) 具有二叉搜索树的优良性质。

所以如果当前节点 \(u\) 的权值小于 \(k\) 那么它的左子树也全部小于 \(k\) 所以直接将这个子树加入 \(l\) 就好了，但是这个时候 \(u\) 的右子树可能会大于等于 \(k\) 所以我们还是要遍历右边的，反之亦然。

比如上面那个图：
先遍历 \(5\)，注意到 \(5<7\) 所以 \(l=\{1,4,5\}\)。

现在左子树都处理完了，看看右子树：
- 再遍历 \(9\) 注意到 \(9\ge 7\) 所以 \(r=\{9\}\)。
  - 最后是 \(7\) 注意到 \(7\ge 7\) 所以 \(r=\{7,8,9\}\)。

好了，来看看代码：

:::success[Code]

inline pair<int,int>split(rint u,rint k)//当前节点和要分裂的权值，返回分裂后两个的根节点编号
{
    if(!u) return {0,0};
    if(tr[u].x<k)//当前节点的权值小于分裂值
    {
        //根据二叉搜索树的性质，这个节点的左子树都小于它，所以左子树都<k，但是我们不知道右子树有没有可能>=k所以递归看看
        auto x=split(tr[u].r,k);
        tr[u].r=x.first;
        pushup(u);//计算子树大小
        return {u,x.second};
    }
    else//反之亦然
    {
        auto x=split(tr[u].l,k);
        tr[u].l=x.second;
        pushup(u);
        return {x.first,u};
    }
}

:::

合并

比如我们还是对 \(l\)，\(r\) 两颗二叉搜索树操作，在合并前你必须保证 \(l\) 中每一个节点都要小于等于 \(r\)，这很重要。（蓝色的是随机权值）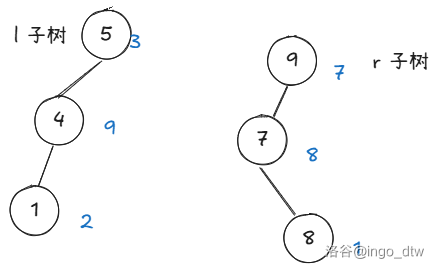

我们由于怕被卡掉所以我们可以将每个节点附加上随机权值，这样合并出来的二叉搜索树也是随机的。

我们遵守一个规律，就是随机值大的做随机值小的节点的子节点。

比如上图，节点 \(5\) 的随机值比 \(9\) 的小，所以 \(9\) 就直接合到右子树去。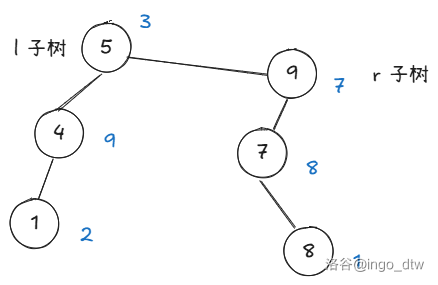

来看看代码：

:::success[Code]

inline int merge(rint l,rint r)//合并 l 和 r，返回合并完的根节点
{
    if(!l||!r) return l|r;//如果有个子树为空，返回另外一个
    if(tr[l].s<tr[r].s)
    {
        tr[l].r=merge(tr[l].r,r);//继续与l子树的右子树比随机值
        pushup(l);
        return l;
    }
    else//反之亦然
    {
        tr[r].l=merge(l,tr[r].l);
        pushup(r);
        return r;
    }
}

:::

插入

现在我们要插入一个节点权值为 \(x\)，怎么办呢？

首先我们考虑直接把 \(x\) 建立成一个树，然后再把原来的 \(\texttt{FHQ-Treap}\) 给分裂（分裂的值取 \(x\)）成 \(l\) 和 \(r\)，最后将 \(l\)，\(x\)，\(r\) 合并就好。

来看看代码：

:::success[Code]

inline void insert(rint x)
{
    tr[++cnt]={0,0,x,(int)(rnd()),1};//没有左子树和右子树子树大小为1
    auto [l,r]=split(root,x);
    root=merge(merge(l,cnt),r);
}

:::

删除

现在要删除一个值为 \(x\) 节点怎么办呢？这个比较好玩。

首先我们先把原来一颗树分为 \(l\)，\(r\) 分别为小于 \(x\) 和大于等于 \(x\) 的，这个时候我们将 \(r\) 分为等于 \(x\) 和大于的。

如果你要把值为 \(x\) 的节点全都删掉，那么直接合并 \(l\) 和 \(r\)；如果你只要删掉一个值为 \(x\) 的节点，那你只需要将等于 \(x\) 的树的左子树和右子树合并，这样你就将根节点删掉了。

看看代码：

:::success[Code]

inline void erase(rint x)
{
    auto [l,r]=split(root,x);
    auto [m,rr]=split(r,x+1);
    if(m)
    {
        m=merge(tr[m].l,tr[m].r);
    }
    root=merge(merge(l,m),rr);
}

:::

查询排名

我们需要查询 \(x\) 的排名，怎么办呢？

直接将树分裂（分裂值为 \(x\)），然后直接返回小于 \(x\) 的子树的字数大小加一就好。

来看看代码：

:::success[Code]

inline int find1(rint x)
{
    auto [l,r]=split(root,x);
    rint ans=tr[l].siz+1;
    root=merge(l,r);
    return ans;
}

:::

查询第 \(k\) 名

还是那张图。

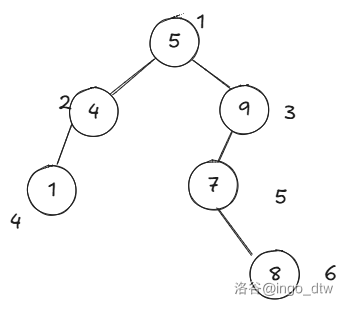
首先，还是根据二叉搜索树的优良性质，所以我们直接不看权值什么的，只看编号。

比如上图，我们需要找到第 \(4\) 大的，我们发现 \(1\) 号节点的右子树大小为 \(2\) 左子树为 \(3\) 显然，在左子树。

于是我们来到 \(3\) 号节点，左子树大小为 \(2\) 右子树为 \(0\)，所以在左子树。

来到 \(5\) 号节点，发现左子树的大小为 \(0\) 是这个这个节点本身。

如果你想问，在 \(3\) 号节点的时候为什么不返回？因为 \(3\) 号节点的排名应该是：\(1\) 号节点左子树的大小加上自己，然后在加上 \(3\) 号节点的左子树。

来看看代码：

:::success[Code]

inline int find2(rint k)
{
    rint pos=root;
    while(pos)
    {
        if(k==tr[tr[pos].l].siz+1) return tr[pos].x;//就是这个节点

        if(k<=tr[pos].siz) pos=tr[pos].l;//在左子树
        else 
        {
            k-=(tr[tr[pos].l].siz+1);//减去其他的方便后面计算
            pos=tr[pos].r;
        }
    }
}

:::

查询前驱

怎么查询前驱呢？那不就是排名比 \(k\) 小 \(1\) 的元素吗？

:::success[Code]

inline int pre(rint x)
{
    return find2(find1(x)-1);
}

:::

查询后继

差询后继和前驱不一样，为什么呢？因为我们的边界问题，我们定义 split 函数时，是分成 \(<x\) 和 \(\ge x\) 两类，如果和前驱一样，查询后继的话，那就是排名比 \(k\) 大 \(1\) 的元素，但是注意到我们 query2 函数，如果有过个相同的值，查询的是最前面的那个。

但是我们可以通过查询比 \(x\) 大 \(1\) 的值的排名的值来找到后继，为什么呢？因为 \(x\) 的后继就是比 \(x\) 大，的最小的那个，假设这个值存在，那它的是什么？没错就是 \(x+1\)。

总结一下，查询前驱可以用查询后继的方法，但是查询后继不可以用查询前驱的方法。

:::success[Code]

inline int nxt(rint x)
{
    return find2(find1(x+1));
}

:::

计算子树大小

和线段树类似，左子树的大小加上右子树的大小加上自己。

:::success[Code]

inline void pushup(rint u)
{
    tr[u].siz=tr[tr[u].l].siz+tr[tr[u].r].siz+1;
}

:::

完整代码

:::success[Ac Code]

#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define rint register int
#define R register
#define _ read<int>()
template<class T>inline T read()
{
    R T r=0,f=1;R char c=gc();
    while(!isdigit(c))
    {
        if(c=='-') f=-1;
        c=gc();
    }
    while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
    return f*r;
}
inline void out(rint x)
{
    if(x<0) pc('-'),x=-x;
    if(x<10) pc(x+'0');
    else out(x/10),pc(x%10+'0');
}
const int N=1e5+10;
int cnt,root;
mt19937 rnd(time(0)*114514/1919810);
struct FHQ_Treap
{
    struct Tree
    {
        int l,r,x,s,siz;
    }tr[N];
    inline void pushup(rint u)
    {
        tr[u].siz=tr[tr[u].l].siz+1+tr[tr[u].r].siz;
    }
    inline pair<int,int>split(rint u,rint k)//当前节点和要分裂的权值，返回分裂后两个的根节点编号
    {
        if(!u) return {0,0};
        if(tr[u].x<k)//当前节点的权值小于分裂值
        {
            //根据二叉搜索树的性质，这个节点的左子树都小于它，所以左子树都<k，但是我们不知道右子树有没有可能>=k所以递归看看
            auto x=split(tr[u].r,k);
            tr[u].r=x.first;
            pushup(u);//计算子树大小
            return {u,x.second};
        }
        else//反之亦然
        {
            auto x=split(tr[u].l,k);
            tr[u].l=x.second;
            pushup(u);
            return {x.first,u};
        }
    }
    inline int merge(rint l,rint r)//合并 l 和 r，返回合并完的根节点
    {
        if(!l||!r) return l|r;//如果有个子树为空，返回另外一个
        if(tr[l].s<tr[r].s)
        {
            tr[l].r=merge(tr[l].r,r);//继续与l子树的右子树比随机值
            pushup(l);
            return l;
        }
        else//反之亦然
        {
            tr[r].l=merge(l,tr[r].l);
            pushup(r);
            return r;
        }
    }
    inline void insert(rint x)
    {
        tr[++cnt]={0,0,x,(int)(rnd()),1};//没有左子树和右子树子树大小为1
        auto [l,r]=split(root,x);
        root=merge(merge(l,cnt),r);
    }
    inline void erase(rint x)
    {
        auto [l,r]=split(root,x);
        auto [m,rr]=split(r,x+1);
        if(m) m=merge(tr[m].l,tr[m].r);
        root=merge(merge(l,m),rr);
    }
    inline int find1(rint x)
    {
        auto [l,r]=split(root,x);
        rint ans=tr[l].siz+1;
        root=merge(l,r);
        return ans;
    }
    inline int find2(rint k)
    {
        rint pos=root;
        while(pos)
        {
            if(k==tr[tr[pos].l].siz+1) return tr[pos].x;//就是这个节点
            if(k<=tr[tr[pos].l].siz) pos=tr[pos].l;//在左子树
            else 
            {
                k-=(tr[tr[pos].l].siz+1);//减去其他的方便后面计算
                pos=tr[pos].r;
            }
        }
        return -1;
    }
    inline int pre(rint x)
    {
        return find2(find1(x)-1);
    }
    inline int nxt(rint x)
    {
        return find2(find1(x+1));
    }
}tr;

signed main()
{
    rint q=_;
    while(q--)
    {
        rint op=_,x=_;
        if(op==1) tr.insert(x);
        else if(op==2) tr.erase(x);
        else if(op==3) 
        {
            out(tr.find1(x));pc('\n');
        }
        else if(op==4)
        {
            out(tr.find2(x));
            pc('\n');
        }
        else if(op==5)
        {
            out(tr.pre(x));pc('\n');
        }
        else
        {
            out(tr.nxt(x));pc('\n');
        }
    }
    return 0;
}

:::

带旋 \(\texttt{Treap}\)

首先，带旋 \(\texttt{Treap}\) 最大的特点就是左旋右旋。

左旋

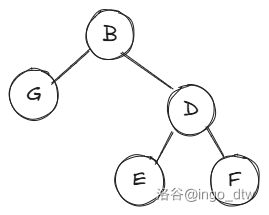
如上图，现在我们把 \(B\) 左旋，这个时候 \(D\) 就成为根结点，然后 \(B\) 要成为 \(D\) 的左子树，但是和 \(E\) 冲突，因为是 BST 所以 \(B\) 肯定小于 \(E\) 所以把 \(E\) 接到 \(B\) 的右子树。

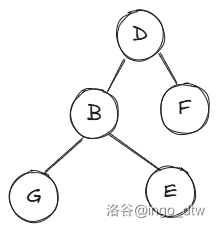
来看看改变了什么，首先根（\(B\)）的右子树（\(D\)）变为其右子树（\(D\)）的左子树（\(E\)），其次根（\(B\)）的右子树（\(D\)）的左子树变为根（\(B\)）。

:::success[Code]

inline int zag(rint u)
{
    rint v=tr[u].r;
    tr[u].r=tr[v].l;
    tr[v].l=u;
    pushup(u);
    pushup(v);
    return v;
}

:::

右旋

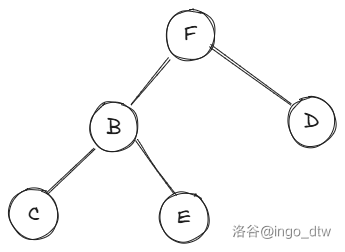
如上图，我们先不管具体的值，只看大小关系，我们需要将它从 \(F\) 那里右旋，将 \(F\) 往下调，于是 \(B\) 变为根节点，但是你发现 \(F>B\) 所以 \(F\) 变为 \(B\) 的右节点，可是 \(B\) 已经有个右节点 \(E\) 了，怎么办呢？注意到已 \(B\) 为根的子树全都小于 \(F\) 所以 \(E\) 应该在 \(F\) 的左子树。

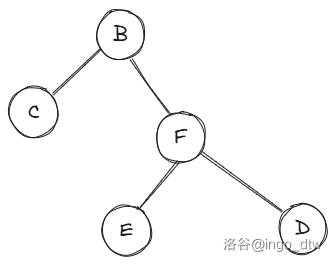
如上图，现在右旋完了，我们对比一下看一下改变了啥，首先就是 \(B\) 的右子树变为以 \(F\) 为根的子树，\(F\) 的左子树从 \(B\) 变为 \(B\) 的右子树。

:::success[Code]

inline int zig(rint u)
{
    rint v=tr[u].l;
    tr[u].l=tr[v].r;
    tr[v].r=u;
    pushup(u);
    pushup(v);
    return v;
}

:::

插入

首先，我们要保证 BST 性质不被破坏，那么我们就按照 BST 性质，找到一个空节点建立这个新插入的点，然后如果破坏了小根堆性质，那么就左旋或者右旋调整过来。

:::success[Code]

inline int insert(rint u,rint x)//当前的点为u，插入值为x的点
{
    if(!u) return neo(x);
    if(x==tr[u].x) tr[u].cnt++;//相等
    else if(x<tr[u].x)
    {
        tr[u].l=insert(tr[u].l,x);
        if(tr[tr[u].l].s>tr[u].s) u=zig(u);//左儿子优先级高，右旋
    }
    else
    {
        tr[u].r=insert(tr[u].r,x);
        if(tr[u].s>tr[tr[u].r].s) u=zag(u);//右儿子优先级高，左旋
    }
    pushup(u);
    return u;
}

:::

删除

这个很有意思，首先我们先根据 BST 的性质，找到这节点，我们分类讨论一下：

如果这个节点不止一个：
- 删掉就好。
如果只有一个：
- 如果是叶子节点：
  - 删掉就好。
- 如果是有一个左节点：
  - 将要删掉的节点左旋，然后就变成叶子节点，删掉就好。
- 如果是有一个右节点：
  - 将要删掉的节点右旋，然后就变成叶子节点，删掉就好。
- 如果两个节点都有：
  - 比较两个节点的优先级，优先级低的左旋或者右旋上去，然后要删掉的节点变成叶子节点，删掉就好。

:::success[Code]

inline int erase(rint u,rint x)
{
    if(!u) return 0;//没这个节点
    if(x<tr[u].x)//在左子树
    {
        tr[u].l=erase(tr[u].l,x);
    }
    else if(x>tr[u].x)//在右子树
    {
        tr[u].r=erase(tr[u].r,x);
    }
    else//就是这个节点
    {
        if(tr[u].cnt>1) tr[u].cnt--;//大于一个
        else
        {
            if(!tr[u].l&&!tr[u].r) return 0;//删掉
            else if(tr[u].l&&!tr[u].r)
            {
                u=zig(u);tr[u].r=erase(tr[u].r,x);//删除，注意到这里不是叶子节点还要继续右旋到叶子节点
            }
            else if(!tr[u].l&&tr[u].r)
            {
                u=zag(u);tr[u].l=erase(tr[u].l,x);//同理
            }
            else 
            {
                if(tr[tr[u].l].s<tr[tr[u].r].s)//左边的小，右旋
                {
                    u=zig(u);tr[u].r=erase(tr[u].r,x);
                }
                else
                {
                    u=zag(u);tr[u].l=erase(tr[u].l,x);
                }                
            }
        }
    }
    pushup(u);
    return u;
}

:::

查询排名

怎么查询 \(x\) 的排名呢？还是按照 BST 的性质找 \(x\)。

找到了：
- 返回之前和加上左子树的大小加上 \(1\)。
如果在左子树：
- 继续找。
如果在右子树：
- 加上左子树和这个节点本身的大小继续找。

:::success[Code]

inline int find1(rint u,rint x)
{
    if(!u) return 1;//没有x这个节点，排名1
    if(x==tr[u].x)
    {
        return tr[tr[u].l].siz+1;//左子树大小加1
    }
    else if(x<tr[u].x)
    {
        return find1(tr[u].l,x);
    }
    else
    {
        return tr[tr[u].l].siz+tr[u].cnt+find1(tr[u].r,x);
    }
}

:::

查询第 \(k\) 小

怎么查询第 \(k\) 小的数呢？和 \(\texttt{FHQ-Treap}\) 有点像，不过我们这次用递归来找。

:::success[Code]

inline int find2(rint u,rint k)
{
    if(!u) return -114514;//没有这个排名
    if(k<=tr[tr[u].l].siz)//在左子树中
    {
        return find2(tr[u].l,k);
    }
    else if(k<=tr[tr[u].l].siz+tr[u].cnt)//就是这个节点
    {
        return tr[u].x;
    }
    else//在右子树
    {
        return find2(tr[u].r,k-tr[tr[u].l].siz-tr[u].cnt);
    }
}

:::

查询前驱

怎么查询 \(x\) 的前驱？我们来分情况讨论一下：

如果当前节点的值大于等于 \(x\)：
- 说明 \(x\) 的前驱在左子树。
否则，查询先查询右子树有没有比 \(x\) 小点的，最后和当前节点取 \(\max\)。

:::success[Code]

inline int pre(rint u,rint x)//查询 x 前驱
{
    if(!u) return -1145141919810;//这个子树中没有 x 前驱
    if(x<=tr[u].x) return pre(tr[u].l,x);//前驱不是右子树和当前节点
    return max(tr[u].x,pre(tr[u].r,x));
}

:::

查询后继

怎么查询 \(x\) 的后继呢？来讨论一下：

如果当前节点小于等于 \(x\)：
- 后继肯定不在左子树或者当前节点，去右子树看看。
如果当前节点大于 \(x\)：
- 去左子树看看大于 \(x\) 的，和当前节点取 \(\min\)。

:::success[Code]

inline int nxt(rint u,rint x)//查询x后继
{
    if(!u) return 1145141919810;//这个子树没有 x 后继
    if(tr[u].x<=x) return nxt(tr[u].r,x);
    return min(tr[u].x,nxt(tr[u].l,x)); 
}

:::

完整代码

:::success[Ac Code]

#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define R register
#define int long long
#define rint register int
#define _ read<int>()
inline bool blank(R const char &x){return !(x^32)||!(x^10)||!(x^13)||!(x^9);}
template<class T>inline T read()
{
    R T r=0,f=1;R char c=gc();
    while(!isdigit(c))
    {
        if(c=='-') f=-1;
        c=gc();
    }
    while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
    return f*r;
}
inline void out(rint x)
{
    if(x<0) pc('-'),x=-x;
    if(x<10) pc(x+'0');
    else out(x/10),pc(x%10+'0');
}
inline void read(R char &x)
{
    for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=1e5+10;
mt19937 rnd(time(0)*114514/1919810);
int root=0;
struct Treap
{
    struct Tree{int l,r,siz,cnt,x,s;}tr[N];
    int cnt;
    inline int neo(rint x)
    {
        tr[++cnt]={0,0,1,1,x,(int)rnd()};
        return cnt;
    }
    inline void pushup(rint u){tr[u].siz=tr[tr[u].l].siz+tr[tr[u].r].siz+tr[u].cnt;}
    inline int zag(rint u)//左旋
    {
        rint v=tr[u].r;
        tr[u].r=tr[v].l;
        tr[v].l=u;
        pushup(u);pushup(v);
        return v;
    }
    inline int zig(rint u)//右旋
    {
        rint v=tr[u].l;
        tr[u].l=tr[v].r;
        tr[v].r=u;
        pushup(u);pushup(v);
        return v;
    }
    inline int insert(rint u,rint x)//当前的点为u，插入值为x的点
    {
        if(!u) return neo(x);
        if(x==tr[u].x) tr[u].cnt++;//相等
        else if(x<tr[u].x)
        {
            tr[u].l=insert(tr[u].l,x);
            if(tr[tr[u].l].s>tr[u].s) u=zig(u);//左儿子优先级高
        }
        else
        {
            tr[u].r=insert(tr[u].r,x);
            if(tr[u].s>tr[tr[u].r].s) u=zag(u);//右儿子优先级第
        }
        pushup(u);
        return u;
    }
    inline int erase(rint u,rint x)
    {
        if(!u) return 0;//没这个节点
        if(x<tr[u].x)//在左子树
        {
            tr[u].l=erase(tr[u].l,x);
        }
        else if(x>tr[u].x)//在右子树
        {
            tr[u].r=erase(tr[u].r,x);
        }
        else//就是这个节点
        {
            if(tr[u].cnt>1) tr[u].cnt--;//大于一个
            else
            {
                if(!tr[u].l&&!tr[u].r) return 0;//删掉
                else if(tr[u].l&&!tr[u].r)
                {
                    u=zig(u);tr[u].r=erase(tr[u].r,x);//删除，注意到这里不是叶子节点还要继续右旋旋到叶子节点
                }
                else if(!tr[u].l&&tr[u].r)
                {
                    u=zag(u);tr[u].l=erase(tr[u].l,x);//同理
                }
                else 
                {
                    if(tr[tr[u].l].s<tr[tr[u].r].s)//左边的小，右旋
                    {
                        u=zig(u);tr[u].r=erase(tr[u].r,x);
                    }
                    else
                    {
                        u=zag(u);tr[u].l=erase(tr[u].l,x);
                    }                
                }
            }
        }
        pushup(u);
        return u;   
    }
    inline int find1(rint u,rint x)
    {
        if(!u) return 1;//没有x这个节点，排名1
        if(x==tr[u].x)
        {
            return tr[tr[u].l].siz+1;//左子树大小加1
        }
        else if(x<tr[u].x)
        {
            return find1(tr[u].l,x);
        }
        else
        {
            return tr[tr[u].l].siz+tr[u].cnt+find1(tr[u].r,x);
        }
    }
    inline int find2(rint u,rint k)
    {
        if(!u) return -114514;//没有这个排名
        if(k<=tr[tr[u].l].siz)//在左子树中
        {
            return find2(tr[u].l,k);
        }
        else if(k<=tr[tr[u].l].siz+tr[u].cnt)//就是这个节点
        {
            return tr[u].x;
        }
        else//在右子树
        {
            return find2(tr[u].r,k-tr[tr[u].l].siz-tr[u].cnt);
        }
    }
    inline int pre(rint u,rint x)//查询 x 前驱
    {
        if(!u) return -1145141919810;//这个子树中没有 x 前驱
        if(tr[u].x>=x) return pre(tr[u].l,x);//前驱不是右子树和当前节点
        return max(tr[u].x,pre(tr[u].r,x));
    }
    inline int nxt(rint u,rint x)//查询x后继
    {
        if(!u) return 1145141919810;//这个子树没有 x 后继
        if(tr[u].x<=x) return nxt(tr[u].r,x);
        return min(tr[u].x,nxt(tr[u].l,x)); 
    }
}tr;

signed main()
{  
    rint q=_;
    while(q--)
    {
        rint op=_,x=_;
        if(op==1)
        {
            root=tr.insert(root,x);
        }
        else if(op==2)
        {
            root=tr.erase(root,x);
        }
        else if(op==3)
        {
            out(tr.find1(root,x));pc('\n');
        }
        else if(op==4)
        {
            out(tr.find2(root,x));pc('\n');
        }
        else if(op==5)
        {
            out(tr.pre(root,x));pc('\n');
        }
        else 
        {
            out(tr.nxt(root,x));pc('\n');
        }
    }
    return 0;
}

:::

总结

个人认为这两种 \(\texttt{Treap}\) 各有各的优点，\(\texttt{FHQ-Treap}\) 简单易上手，可持久化、区间操作比较简单，带旋 \(\texttt{Treap}\) 左旋右旋个人感觉比较难理解，不过它常数比 \(\texttt{FHQ-Treap}\) 小（也许是我写法的问题），实际解决问题中，还是按需选择吧。

upd

2026/2/8：感谢 @JasmineCloud__ 指出的错误，已修正。

欢迎各位指出我的错误！

posted @ 2026-01-13 19:12 ingo_dtw 阅读(14) 评论(0) 收藏举报

刷新页面返回顶部

满穗欢迎你~

I_love_Man_sui

浅析 FHQ-Treap&Treap

前言

二叉搜索树（BST）

\(\texttt{FHQ-Treap}\)

分裂

合并

插入

删除

查询排名

查询第 \(k\) 名

查询前驱

查询后继

计算子树大小

完整代码

带旋 \(\texttt{Treap}\)

左旋

右旋

插入

删除

查询排名

查询第 \(k\) 小

查询前驱

查询后继

完整代码

总结

upd

公告