浅析字典树（trie）

1 引入

先给出一个问题：给出若干字符串 \(s\)，最后给定一个 \(t\)，求有多少个 \(s\) 是 \(t\) 的前缀？

观察一下这个问题，显然当给出的 \(s\) 数量多，\(t,s\) 长度大，暴力显然会超时。

这个时候我们可以考虑对于这些 \(s\) 建立一颗树，我们叫做字典树。

2 正文

2.1 Trie

怎么建立一颗字典树呢？我们可以把每个字母都变成边权，根到当前节点的路径就是一个字符串，特别的我们可以把 \(s\) 结尾的那个节点打上标记表示从根节点到这个节点的路径形成的字符串就是 \(s\)。

比如我们需要将 \(ac\)，\(wa\)，\(awap\)，\(ms\)，\(l\) 这些字符串建立一颗字典树：

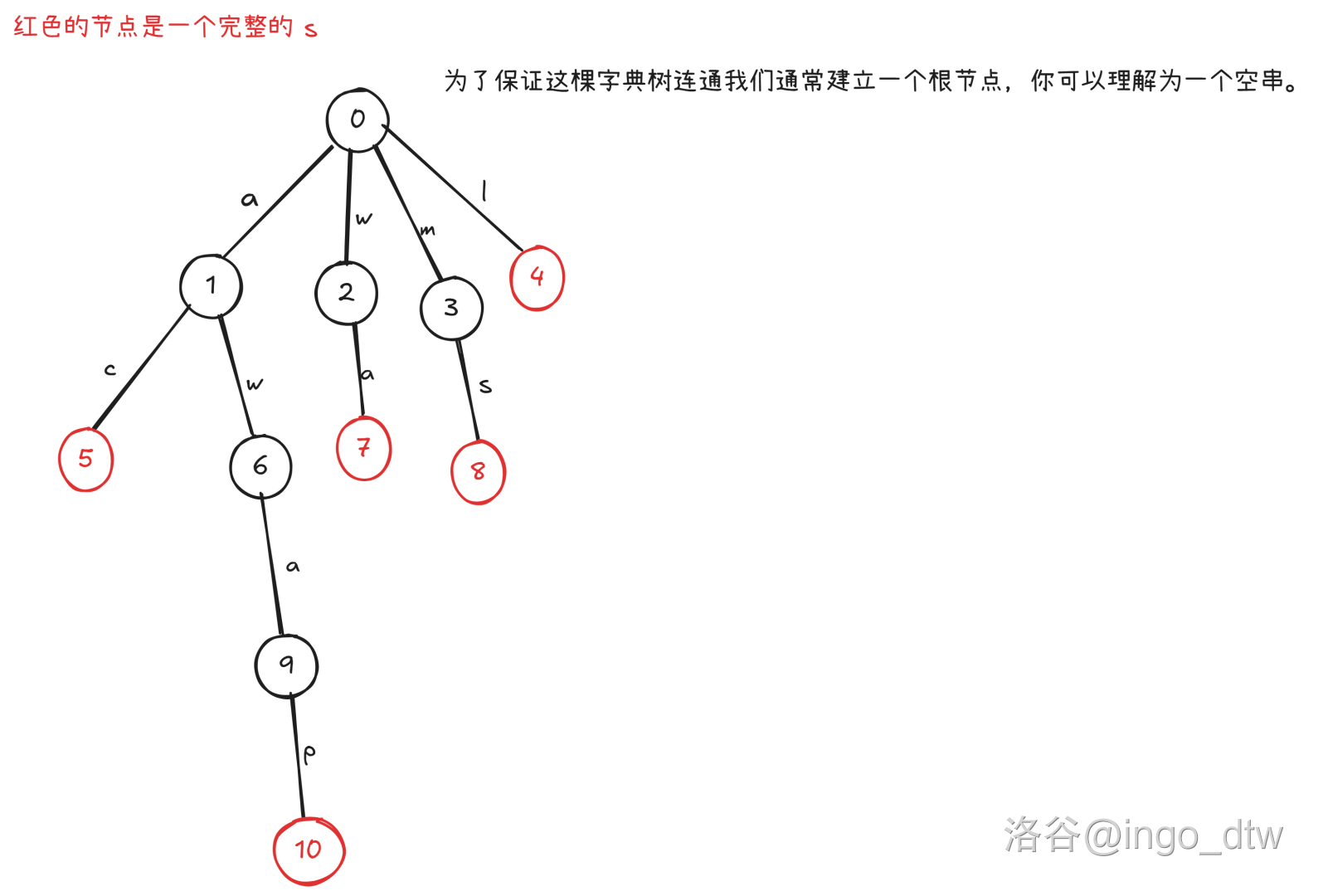
于是我们按照 \(t\) 里的字符对应的边进行遍历，当这个点是某个完整字符串时我们就将答案加上。（如果有多个相同的话直接开个 int 数组遍历到就加上就行）

建立这树的话我们可以用一个数组存下按照我的习惯我就用 nxt 这个数组，具体的可以看看下面的代码：

首先是插入：

Code 1

inline void insert(string s)
{
    int p=0;
    for(int i=0;i<s.size();i++)
    {
        int c=s[i]-'a';
        if(!nxt[p][c]) nxt[p][c]=++cnt;//如果这个节点没被创建
        p=nxt[p][c];
    }
    vis[p]++;//这个节点是个完整的字符串
}

:::
查询：

Code 2

inline int query(string t)
{
    int p=0,ans=0;
    for(int i=0;i<t.size();i++)
    {
        int c=t[i]-'0';
        if(!nxt[p][c]) break;//没有这个节点
        p=nxt[p][c];
        ans+=vis[p];//加上贡献
    }
    return ans;
}

P8306 【模板】字典树。

和上面的差不多，只不过是多次询问。

吗？错！再仔细看看题面，发现他问的是对于每一个 \(t_i\) 有多少 \(s_j\) 满足 \(t_i\) 是 \(s_j\) 的前缀。

我们换个思路 \(vis\) 记录这个节点是多少个 \(s\) 的前缀。

对于查询我们之间返回最后遍历到的节点的 \(vis\) 就行，至于遍历时没有这个节点的话就直接 return 0。

别用 #define int long long，别用 memset。

Ac Code

#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define R register
// #define int long long
#define rint register int
#define _ read<int>()
inline bool blank(R const char &x){return !(x^32)||!(x^10)||!(x^13)||!(x^9);}
template<class T>inline T read()
{
    R T r=0,f=1;R char c=gc();
    while(!isdigit(c))
    {
        if(c=='-') f=-1;
        c=gc();
    }
    while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
    return f*r;
}
inline void out(rint x)
{
    if(x<0) pc('-'),x=-x;
    if(x<10) pc(x+'0');
    else out(x/10),pc(x%10+'0');
}
inline void read(R char &x)
{
    for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=3e6+10;
inline int z(const char &c)
{
    if(c>='a'&&c<='z') return c-'a';
    if(c>='A'&&c<='Z') return c-'A'+26;
    return c-'0'+52;
}
struct trie//我习惯用封装的字典树
{
    int nxt[N][63],cnt,vis[N];//如果每个节点都有26条边的话就可能有 N（节点数）*26 个节点
    inline void insert(string s)
    {
        rint p=0;
        for(rint i=0;i<s.size();i++)
        {
            rint c=z(s[i]);
            if(!nxt[p][c]) nxt[p][c]=++cnt;
            p=nxt[p][c];
            vis[p]++;
        }
    }
    inline int query(string t)
    {
        rint p=0;
        for(rint i=0;i<t.size();i++)
        {
            rint c=z(t[i]);
            if(!nxt[p][c]) return 0;
            p=nxt[p][c];
        }
        return vis[p];
    }
    inline void init()//多测清空别用memset
    {
        for(rint i=0;i<=cnt;i++) 
        {
            for(rint j=0;j<63;j++) nxt[i][j]=0;
        }
        for(rint i=0;i<=cnt;i++) vis[i]=0;
        cnt=0;
    }
}tr;
signed main()
{  
    rint t=_;
    while(t--)
    {
        rint n=_,q=_;
        for(rint i=1;i<=n;i++)
        {
            string s;
            cin>>s;
            tr.insert(s);
        }
        while(q--)
        {
            string t;
            cin>>t;
            out(tr.query(t));
            pc('\n');
        }
        tr.init();
    }
    return 0;
}

2.2 01-Trie

01-Trie 是什么呢？顾名思义就是把一个数分解成二进制然后对于这个二进制串建立一颗字典树。

那么这个 01-Trie 可以解决什么问题呢？比如：

P10471 最大异或对 The XOR Largest Pair

观察一下题面，显然 \(\mathcal{O}(n^2)\) 的暴力十分好打，但是会超时，怎么办呢？

我们先讲题目给出的 \(A\) 里的元素全部插入字典树，再 \(\mathcal{O}(n)\) 的遍历，对于每一个 \(A_i\) 我们贪心查询他在字典树上的最优路径。

我们发现个性质：由于按位异或的运算规则是相同的为 \(0\)，不相同为 \(1\)，所以我们从高位到低位的插入一个数的 01 串，然后查询的时候如果有不同的就尽量选不同的如果这是第 \(i\) 位不同，贡献就是 \(2^i\)，考虑不同发现对于相同也只是没贡献，容易证明以上的贪心策略是正确的。

题目中保证 \(0\le A_i < 2^{31}\) 所以枚举有多少位的时候直接从 \(31\) 到 \(0\) 枚举就好（最后注意到最坏情况下每个节点都被创建每个数最多 \(31\) 位 \(10^5\) 个数，最坏的话空间要开 \(3.1\times 10^6\)）。

学过 LCA 的朋友肯定知道，对于一颗树我们记 \(dis_u\) 是从根到 \(u\) 这个节点的和，那么 \(u\) 到 \(v\) 的最短路是 \(dis_u+dis_v-2\times dis_{\operatorname{LCA}(u,v)}\) 那么异或也一样，但是我们发现就是对于 \(dis_{\operatorname{LCA}(u,v)}\) 这个在异或的时候因为两个相同为 \(0\) 所以就不用再异或个 \(dis_{\operatorname{LCA}(u,v)}\) 了，直接考虑每个节点的最大异或和，和上面的一样。

具体的我们可以先求出每个 \(dis\) 然后再对于每个节点考虑字典树上的最优路径。

Ac Code

#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define R register
// #define int long long
#define rint register int
#define _ read<int>()
inline bool blank(R const char &x){return !(x^32)||!(x^10)||!(x^13)||!(x^9);}
template<class T>inline T read()
{
    R T r=0,f=1;R char c=gc();
    while(!isdigit(c))
    {
        if(c=='-') f=-1;
        c=gc();
    }
    while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
    return f*r;
}
inline void out(rint x)
{
    if(x<0) pc('-'),x=-x;
    if(x<10) pc(x+'0');
    else out(x/10),pc(x%10+'0');
}
inline void read(R char &x)
{
    for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=3.1e6+10;
int a[N],dis[N];
vector<pair<int,int>>g[N];
struct trie//我习惯用封装的字典树
{
    int nxt[N][2],cnt,vis[N];
    inline void insert(rint s)
    {
        rint p=0;
        for(rint i=31;i>=0;i--)
        {
            rint c=(s>>i)&1;//这一位是0还是1
            if(!nxt[p][c]) nxt[p][c]=++cnt;
            p=nxt[p][c]; 
        }
    }
    inline int query(rint t)
    {
        rint p=0,ans=0;
        for(rint i=31;i>=0;i--)
        {
            rint c=(t>>i)&1;
            if(nxt[p][c^1]) ans+=(1<<i),p=nxt[p][c^1];//如果有不同的直接走不同的
            else p=nxt[p][c];//为什么没有这一位相同不相同都没有的情况？因为这个数本身插入的时候一定创建了一个不同的
        }
        return ans;
    }

}tr;
inline void dfs(rint u,rint fa)
{
    for(auto qwq:g[u])  
    {
        rint v=qwq.first,w=qwq.second;
        if(v==fa) continue;
        dis[v]=dis[u]^w;
        dfs(v,u);
    }
}
signed main()
{  
    rint n=_;
    for(rint i=1;i<n;i++)
    {
        rint u=_,v=_,w=_;
        g[u].push_back({v,w});
        g[v].push_back({u,w});
    }
    dfs(1,0);
    for(rint i=1;i<=n;i++) tr.insert(dis[i]);
    rint ans=0;
    for(rint i=1;i<=n;i++)
    {
        ans=max(ans,tr.query(dis[i]));
    }
    out(ans);
    return 0;
}

:::