浅析 Manacher
luogu食用更佳。
模拟赛被 Manacher 创飞了, 所以重拾 Manacher。
前言
先问你个问题:给定一个字符串 \(s\),如何在线性时间复杂度以内求出 \(s\) 的子串 \(t\) 保证 \(t\) 回文,使得 \(t\) 长度最大?请你求出这个长度。(当 \(t=t_{\text{rev}}\) 时,\(t\) 是回文串,\(t_{\text{rev}}\) 是 \(t\) 的反转字符串)
注意到回文串最多 \(\mathcal{O}(n)\) 个所以可以枚举每一个回文串的回文中心然后再枚举这个回文串的长度,时间复杂度最坏 \(\mathcal{O}(n^2)\)。
while(i+p[i]<=n&&i-p[i]>=1&&s[i+p[i]]==s[i-p[i]]) p[i]++;
\(p_i\) 表示已 \(s_i\) 为回文中心的最长回文半径。
但是这样对于 \(n\ge 10^5\) 显然会超时(假设 \(n=|s|\),\(|s|\) 是 \(s\) 的长度),不过我们可以通过哈希 + 二分 \(\mathcal{O}(n\log n)\) 解决,或者使用后缀数组和快速 LCA \(\mathcal{O}(n)\) 解决,不过这些我都不会 而且这些算法不是多个 \(\log\) 就是常数较大,所以我们可以考虑使用 Manacher 解决,且时间空间复杂度都为 \(\mathcal{O}(n)\)。
正文
Manacher 由 Glenn K. Manacher 在 1975 年提出。
原文:link。
中文翻译(由 deepseek 完成):link。
首先你得明白一个特性
如果 \(s_{l\dots r}\) 是回文串的话 \(mid\) 是他们的回文中心,那么 \(s_{l\dots mid-1}=s_{mid+1\dots r}\) 你可以自己模拟一下比如:
\(abababa\) 显然是一个回文串 \(l=1\),\(r=7\),\(mid=4\)。
显然 \(s_{1\dots 4-1=3}=aba=s_{4+1=5\dots 7}=aba\)。
我们可以考虑维护 \(l\),\(r\) 和一个 \(mid\) 这三个变量:
- \(l\) 表示某一个回文中心减上回文半径的最小值的位置。
- \(r\) 表示某一个回文中心加上回文半径的最大值的位置。
- \(mid\) 就是这个最大的 \(r\) 和最小的 \(l\) 其对应的回文中心。
注意到一个回文串最大的性质就是对称于是我们考虑从对称性质入手来优化上面这个代码。
如果你注意力惊人的话,就可以注意到如果现在需要知道 \(p_i\) 的值,前面的 \(p_{1\dots i-1}\) 并非没有作用,我们可以这么计算 (\(j\) 在当前的最大的 \(r\) 情况下 \(s_{l\dots r}\) 中关于 \(i\) 的对称点,下文有解释):
- 如果 \(i+p_j\le r\),那么我们选择朴素算法:
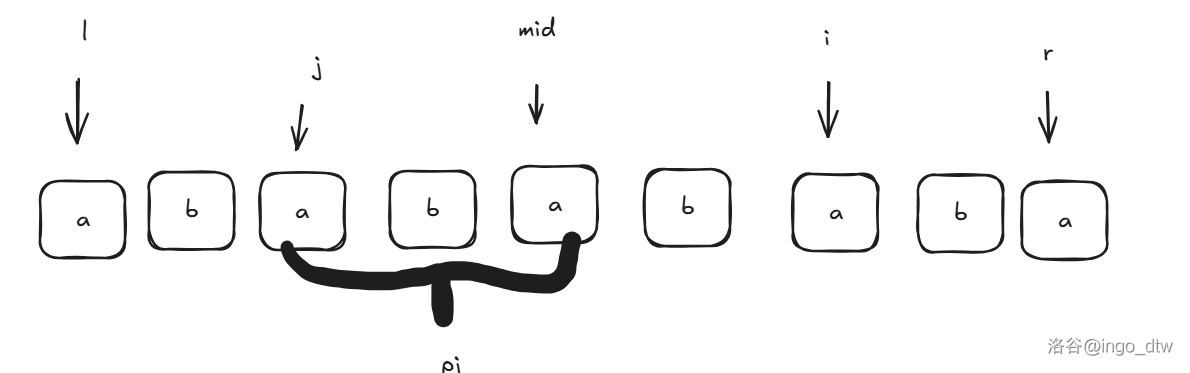
那么在上图,\(p_i=p_j\) 为什么呢?因为 \(s_{j\dots mid}=s_{mid\dots i}\) 这很明显吧,那么如果 \(j-p_j\ge l\) 也就是已 \(j\) 为回文中心的回文串在以 \(mid\) 为回文中心的回文串内,那么你发现 \(s_{j-p_j\dots j}=s_{i\dots i+p_j}\) 相等(因为他们在 \(s_{l\dots r}\) 这个回文串内,因为回文所以相等),所以 \(p_i\) 至少等于 \(p_j\)。 - 如果 \(i+p_j>r\):
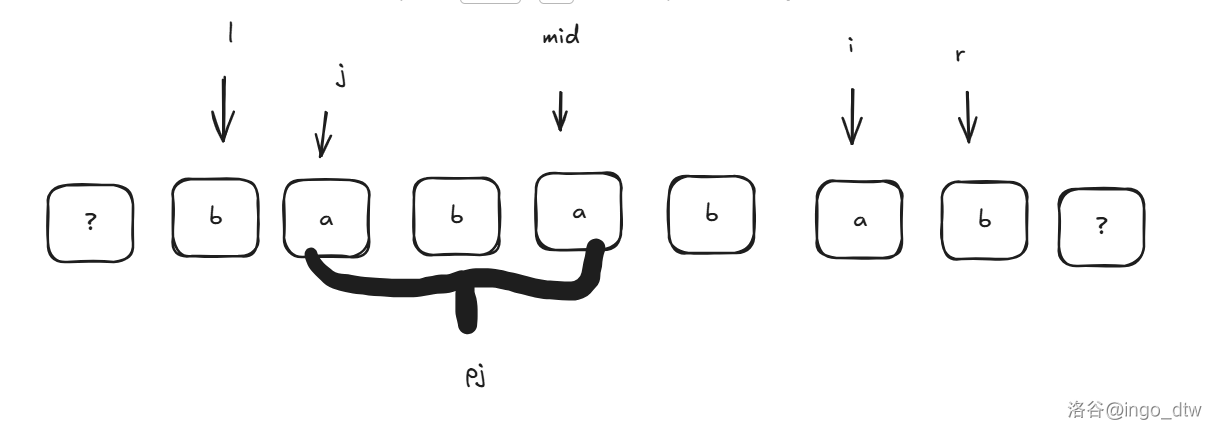
这个时候 \(s_{j-p_j\dots j}\) 和 \(s_{i\dots i+p_j}\) 就不一定相等,因为 \(i+p_j> r\) 的位置我们不知道是不是相等,但是我们通过上面的图发现:
所以如果 \(i\le r\) 那么(\(j=2\times mid-i\)):
注意到 \(l=mid-(r-mid)\) 而且并没啥用,所以实际实现中只需维护 \(r\)。
为什么 \(j=2\times mid -i\)
来解释一下为什么 \(j=2\times mid-i\) 因为 \(j\) 是 \(i\) 关于 \(mid\) 的对称点(也就是 \(s_{i\dots j}\) 的回文中心是 \(mid\))那么显然:\(\frac{i+j}{2}=mid\) 所以我们化简一下:\(i+j=2 \times mid\) 移下项:\(j=2\times mid -i\)
然后我们再暴力扩展,代码就为:
Code
for(int i=1;i<=n;i++)
{
if(i<=r) p[i]=min(p[2*mid-i],r-i+1);
else p[i]=0;
while(i-p[i]>=1&&i+p[i]<=n&&s[i-p[i]]==s[i+p[i]]) p[i]++;//暴力拓展
if(i+p[i]>r) r=i+p[i],mid=i;//比r还大就用这个
ans=max(ans,p[i]);//记录最大的
}
答案为 \(ans\times 2+1\)。
但是不难发现以上这个只能统计长度为奇数的回文串,无法统计长度为偶数的,我们可以考虑加上边界字使得都可以统计。
怎么加呢?我们将每个字符之间都加一个隔断符,这样不管是奇数还是偶数就都可以统计(因为偶数就是枚举到分隔符然后做上面的过程)但是我们的代码也要改一下改成:
Code
for(int i=1;i<=n;i++)
{
if(i<=r) p[i]=min(p[2*mid-i],r-i+1);
else p[i]=1;
while(i-p[i]>=1&&i+p[i]<=n&&s[i-p[i]]==s[i+p[i]]) p[i]++;//暴力拓展
if(i+p[i]-1>r) r=i+p[i]-1,mid=i;//比r还大就用这个
ans=max(ans,p[i]);//记录最大的
}
答案为 \(ans-1\) 因为分隔符的存在使得 \(p_i\) 本来就大了一倍多一个。
注意到 \(r\) 单调递增,且拓展次数总和不可能超过 \(n\) 故时间复杂度线性。
我们来道例题:
P3805 【模板】Manacher
Ac Code
#include <bits/stdc++.h>
using namespace std;
const int N=3*11e6+10;//相邻两个字符要加一个符号所以开3倍空间最保险
char s[N];
int p[N],mid,r,cnt;
int main()
{
string c;//初始字符串
cin>>c;
s[++cnt]=' ';
s[++cnt]='#';
for(char ch:c)
{
s[++cnt]=ch,s[++cnt]='#';//相邻两个字符之间加个 # 保证回文串是个长度为奇数的字符串
}
s[++cnt]='!';//最后也加一个防止越界(下面的暴力拓展我没判边界了)
int ans=0;
for(int i=2;i<cnt;i++)
{
if(i<=r) p[i]=min(p[2*mid-i],r-i+1);//有对称点
else p[i]=1;//初始回文半径为1
while(s[i-p[i]]==s[i+p[i]]) p[i]++;//暴力拓展
if(i+p[i]-1>r) mid=i,r=i+p[i]-1;//如果这个回文串的右端点比r大就更新mid和r
ans=max(ans,p[i]);//最长的回文半径
}
cout<<(ans-1);//由于我们将每个字符之间都加个了#所以答案要减1
return 0;
}
我们再来做一道习题:
P1659 [国家集训队] 拉拉队排练
由题意可知我们只需要统计长度为奇数的回文串的长度给乘起来,再对 \(19930726\) 取模就行,于是你一交,直接 TLE 注意一下数据范围 \(1\le k \le 10^{12}\) 所以我们考虑快速幂,我们开个桶把回文长度给记一下,再从大到小枚举 \(n\)(注意偶数不要枚举)将长度为 \(i\) 的回文串快速幂就好了。最后这个题只需要统计奇数回文串所以我们可以不用加一些边界字符。
Ac Code
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define R register
#define int long long
#define rint register int
#define _ read<int>()
inline bool blank(R const char &x){return !(x^32)||!(x^10)||!(x^13)||!(x^9);}
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
inline void read(R char &x)
{
for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=1e7+10,MOD=19930726;
char s[N];
int p[N],ct[N],mid,r;
inline int qpow(rint x,rint y)
{
if(x==1) return 1;
rint ans=1;
while(y)
{
if(y&1) ans=(ans*x)%MOD;
x=(x*x)%MOD;
y>>=1;
}
return ans;
}
signed main()
{
rint n=_,k=_;
scanf("%s",s+1);
for(rint i=1;i<=n;i++)
{
if(i<=r) p[i]=min(p[2*mid-i],r-i);
else p[i]=1;
while(i-p[i]>=0&&i+p[i]<=n&&s[i-p[i]]==s[i+p[i]]) p[i]++;
if(i+p[i]>r) mid=i,r=i+p[i];
ct[2*p[i]-1]++;
}
rint sum=0,ans=1;
if(!(n&1)) --n;
for(rint i=n;i>=1;i-=2)
{
sum+=ct[i];
if(sum>k)
{
ans=ans*qpow(i,k)%MOD;
break;
}
else
{
ans=ans*qpow(i,sum)%MOD;
k-=sum;
}
}
if(sum<k) puts("-1");
else out(ans);
return 0;
}
P3501 [POI 2010] ANT-Antisymmetry
对一个 \(0/1\) 串,求出他有多少个子串满足异或之前和异或之后拼接起来是个回文串,我们考虑 Manacher 注意到只需要对给定的字符串求出所有的回文半径加和就是答案,而且只有偶数长度的子串才算入答案,注意拓展的时候是异或(分隔符的直接判不用异或)。
所以答案就是:
除二是因为有分隔符,而且你发现一个回文中心的回文半径就是这个回文串能贡献的答案。(因为只有偶数串成立)
为了方便,我们就不特判分隔符不异或了,直接建立一个数组 \(to_1=0\),\(to_0=1\),\(to_{\texttt{分隔符}}=\texttt{分隔符}\),这样就不用那么麻烦了。
Ac Code
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define R register
#define int long long
#define rint register int
#define _ read<int>()
inline bool blank(R const char &x){return !(x^32)||!(x^10)||!(x^13)||!(x^9);}
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
inline void read(R char &x)
{
for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=5e6+10;
char s[3*N],to[2000];
int cnt,p[N];
signed main()
{
rint n=_;
string str;
cin>>str;
s[0]='!';
s[++cnt]='#';
for(char c:str)
{
s[++cnt]=c;
s[++cnt]='#';
}
s[++cnt]='!';
to['1']='0',to['0']='1',to['#']='#';
rint ans=0,mid=0,r=0;
for(rint i=1;i<=cnt;i+=2)
{
if(i<=r) p[i]=min(p[(mid<<1)-i],r-i+1);
else p[i]=1;
while(s[i-p[i]]==to[s[i+p[i]]]) p[i]++;
if(i+p[i]-1>r) r=i+p[i]-1,mid=i;
ans+=(p[i]>>1);
}
out(ans);
return 0;
}
:::
P6216 回文匹配
考虑先跑一遍 Manacher 然后对于所有奇数回文串暴力跑 KMP 时间复杂度明显 \(\mathcal{O}(n^2)\) 无法通过。
注意到,其实我们可以先跑一遍 KMP 记录所有在 \(s_1\) 中 \(s_2\) 出现的位置,用一个数组存一下 \(vis_i\) 表示 \(s_2\) 在 \(s_1\) 的第 \(i\) 个字符出现了。
现在考虑一下贡献怎么 \(\mathcal{O}(1)\) 计算,我们发现 \(s_{l \dots r}\) 这个子串是回文的话对于答案的贡献是:
但是这有个问题,就是如果这个 \(s_2\) 出现的地方不在某一个求和区间内的话就不可以加。
不过这也是可以计算的,而且如果你真的枚举求上面的式子,那你就要完蛋了,因为这是真的会退化成 \(\mathcal{O}(n^2)\) 但是我们注意到 \(vis_i\) 如果为 \(1\) 的话对于答案的贡献就是 \(i-l+1\),因为他的贡献是他可以向外拓展的长度,比如:
abcabc
ca
\(vis_3=1\),显然答案为 \(i-l+1=3-1+1=3\)。
答案为:
(注意到第二个求和其实等于 \(\sum_{l=1}^rvis_i\times l\))
这个只是一边的,还有另一边,就不写了差不多。
显然做 \(vis_i\) 和 \(vis_i\times i\) 的前缀和就可以求出。
(这个题边界真的很麻烦,容易被绕晕 我恨计数,但是这个题还是有点好处的因为只要奇数回文串,所以不需要加边界字符。)
Ac Code
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define R register
#define int unsigned int//和 2^32 取模直接 uint
#define rint register int
#define _ read<int>()
inline bool blank(R const char &x){return !(x^32)||!(x^10)||!(x^13)||!(x^9);}
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
inline void read(R char &x)
{
for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=6e6+10;
int nxt[N],f[N],sum[N],pre[N],p[N],cnt;
bitset<N>vis;
signed main()
{
rint n=_,m=_;
string s,ss;
cin>>s>>ss;
s=' '+s,ss=' '+ss;
for(rint i=2,j=0;i<=m;i++)
{
while(j&&ss[j+1]!=ss[i]) j=nxt[j];
if(ss[j+1]==ss[i]) j++;
nxt[i]=j;
}
s[0]='!',s[n+1]='~';
for(rint i=1,j=0;i<=n;i++)
{
while(j&&(j==m||s[i]!=ss[j+1])) j=nxt[j];
if(s[i]==ss[j+1]) j++;
if(j==m)
{
vis[i-m+1]=1;
}
}//KMP
for(rint i=1;i<=n;i++) sum[i]=sum[i-1]+vis[i],pre[i]=pre[i-1]+vis[i]*i;//前缀和
rint r,mid;
r=mid=0;
for(rint i=1;i<=n;i++)//Manacher
{
if(i<r) p[i]=min(p[2*mid-i],r-i);
else p[i]=1;
while(s[i+p[i]]==s[i-p[i]]) p[i]++;
if(i+p[i]>r) r=i+p[i],mid=i;
}
for(rint i=1;i<=n;i++) p[i]--;//全部-1方便后面处理
rint ans=0;
for(rint i=1;i<=n;i++)
{
if(2*p[i]+1<m) continue;//回文串还没s2长
rint l=i-(p[i]),r=i+(p[i]);//我没加边界字符所以直接减就好
r=r-m+1;//处理右边界不包含全的情况
if(l>r)continue;
rint mid=l+r>>1;
ans+=(pre[mid]-pre[l-1])-(sum[mid]-sum[l-1])*(l-1);
if(mid<r) ans+=(sum[r]-sum[mid])*(r+1)-(pre[r]-pre[mid]);
}
out(ans);
return 0;
}
其他习题:
读者可以自行练习,如果有不会的话,可以私信我哦。
link。
其他回文串算法
既然聊到回文也来讲讲回文串吧,实际使用中,关于回文串一般就三个:Manacher,PAM,二分 + hash。
首先是 Manacher 上文讲了,就不赘述了,PAM 回文自动机我也不讲主要是 我不会 而且这玩意常数挺大。
二分 + hash
我们可以枚举每一个点然后二分回文半径,再用 hash \(\mathcal{O}(1)\) 判断,显然回文半径是有单调性的,好了现在又有个问题,就是长度为偶数的回文串怎么办?其实这个问题上文已经提到了,就是加一些边界字符使得他们都是长度为奇数的回文串,还有不懂你还可以看看代码。
还有个问题就是判断回文串时,需要比较左半段的反序和右半段的正序。
Code
#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define R register
#define int long long
#define rint register int
#define _ read<int>()
inline bool blank(R const char &x){return !(x^32)||!(x^10)||!(x^13)||!(x^9);}
template<class T>inline T read()
{
R T r=0,f=1;R char c=gc();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=gc();
}
while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
return f*r;
}
inline void out(rint x)
{
if(x<0) pc('-'),x=-x;
if(x<10) pc(x+'0');
else out(x/10),pc(x%10+'0');
}
inline void read(R char &x)
{
for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int B=131;
const int N=3e7+10;
unsigned long long b[N],in[N],a[N];
int cnt,p[N];
char s[N];
inline bool check(rint x, rint i)
{
if (i-x<1||i+x>cnt) return 0;
unsigned long long lh = a[i-x] - a[i] * in[x];
unsigned long long rh = b[i+x] - b[i] * in[x];
//[l,r]=b[r]-b[l-1]*in[r-l+1]
return lh==rh;
}
signed main()
{
string str;
cin>>str;
s[0]='~',s[++cnt]='#';
for(char c:str)
{
s[++cnt]=c;
s[++cnt]='#';
}
in[0]=1;
for(rint i=1;i<=cnt;i++)
{
b[i]=b[i-1]*B+s[i];
in[i]=in[i-1]*B;
}
for(rint i=cnt;i;i--)
{
a[i]=a[i+1]*B+s[i];
}
rint ans=0;
for(rint i=1;i<=cnt;i++)
{
rint l=1,r=min(cnt-i,i),mid,anss=0;
while(l<=r)
{
mid=l+r>>1;
if(check(mid,i))
{
l=mid+1;
anss=mid;
}
else
{
r=mid-1;
}
}
p[i]=anss;
ans=max(ans,p[i]);
}
out(ans);
return 0;
}
与其他回文串算法的区别
-
中心拓展法:就是枚举一个点然后向两边拓展,实现就是我上面写的暴力。
- 这个算法的优势就是空间复杂度 \(\mathcal{O}(1)\) 而且实现简单易理解,但是时间复杂度很高 \(\mathcal{O}(n^2)\) 很多情况下只是暴力。
-
动态规划:我们可以考虑区间 DP 来解决回文串问题,定义 \(dp_{i,j}\) 为 \(s_{i\dots j}\) 的回文串最大长度,则动态转移方程为:
-
如果 \(s_i=s_j\) 那么 \(dp_{i,j}=dp_{i+1,j-1}\)
- 时间复杂度 \(\mathcal{O}(n^2)\),空间复杂度 \(\mathcal{O}(n^2)\)。
- 但是动态规划可以解决如询问 \(l\dots r\) 回文串最大长度可以 \(\mathcal{O}(n^2)\) 预处理,\(\mathcal{O}(1)\) 回答。
-
-
Manacher:前面两个一个好理解一个可以 \(\mathcal{O}(1)\) 查询,但是时间复杂度 \(\mathcal{O}(n^2)\) 无疑是硬伤,但是 Manacher 可以 \(\mathcal{O}(n)\) 的时间复杂度来解决这个问题,这就是 Manacher 最大的优势。
-
关于回文串其实还有个更强大的算法:PAM(
我不会)这个可以统计很多其他的信息,而且算一种在线算法,Manacher 我认为不算,但是注意如果出题人真的想让你用 Manacher 的话一般会卡掉 PAM 虽然 PAM 时间复杂度也是 \(\mathcal{O}(n)\) 但是常数大。 -
二分 + hash:这个主要是多了个 \(\log n\) 而且 hash 常数会有点大。
总结
看到这里相信你对 Manacher 已经有点自己的认知了,其实用不用 Manacher 很好辨别,因为 Manacher 只能用于解决回文串问题,对于一道 Manacher 的题一般都是让你观察 Manacher 实现的性质(如 \(p\) 数组统计回文半径),然后来解决这道题。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号