浅析 Tarjan

0. 前言

要学 tarjan 你先得了解一些概念，不了解文中的一些概念可以去 oi-wiki 上自行搜索。

在正式开始之前先引入一句机房大佬的名言：

DAG 为什么没有环。

由于本人习惯问题文中的 rint 其实是 register int 的意思，读者可以不用在意。

1 tarjan 求强连通分量

首先你得先了解 DFS 生成树，其实就是对一个图进行 DFS 的时候生成的一颗树，我们称在树上的为树边，不在的为非树边。

tarjan 求强连通分量，一棵子树，其实就是对图进行 DFS 在 DFS 的时候会维护一个栈，对于每个节点会维护如下信息：

• \(dfn_u\) 就是节点 \(u\) 被 DFS 遍历到的顺序，也称时间戳。
• \(low_u\) 从节点 \(u\) 出发，通过有向边能够到达的、还在栈中的所有节点中，最小的 \(dfn\) 值 \(^1\)。

看着 \(low\) 的定义是不是有点看不懂，我也是，但是别着急，我们不妨先来看看 \(low\) 在 tarjan 里起到什么作用，其实 \(low\) 就是个回溯值，在大多数情况下你可以把强连通分量看作一个图的子图环里包含的节点最大是哪个环，但是这样实际是由例外的如：

    A → B
    ↑   ↓
    D ← C
    ↖   ↙
      E

你会发现这个图是由不止 \(1\) 个环构成，所以如果你想更好的理解 \(low\) 值，你不妨理解成由一个及以上个环构成的一个子图其中的节点在 DFS 的时候最早是什么时候被遍历到的。

如果看到现在你还是不明白，没事我们看看 tarjan 的实现过程。在 tarjan 的实现过程中，我们把遍历到的节点都塞到一个栈中并给这个节点打上标记，如果遇到一个没有遍历过的，再尝试 \(low_v\) 来更新 \(low_u\)，如果遍历过那就用 \(dfn_v\) 来尝试更新 \(low_u\) 代码如下 \(^2\)：

:::success[Code]

inline void tarjan(int u,int fa)
{
    dfn[u]=low[u]=++dfn[0];
    sta[++top]=u;//入栈
    vis[u]=1;//打上标记（在栈中）
    for(int v:g[u])
    {
        if(!dfn[v])//没被遍历过
        {
            tarjan(v,u);//就继续遍历
            low[u]=min(low[u],low[v]);
        }
        else if(vis[v]) low[u]=min(low[u],dfn[v]);
    }
}

:::

但是现在我们怎么知道强连通分量的那个节点在 DFS 的过程中最先被遍历到呢（其实也就是这个强连通分量的根节点）？我们发现如果 \(low_u=dfn_u\) 那么就是这个节点最先被遍历到，为什么？因为根据 \(low\) 的定义，我们发现如果 \(dfn_u=low_u\) 说明这个节点没有更早的了，那它不就是最早被访问的吗？所以如果这个节点是根节点，那么我们就可以把栈里的节点都弹了，直到遇到 \(u\) 这个节点，说明这个就形成了一个环，就停止弹栈。完整代码如下：

:::success[code]

inline void tarjan(int u,int fa)
{
    dfn[u]=low[u]=++dfn[0];
    sta[++top]=u;//入栈
    vis[u]=1;//打上标记
    for(int v:g[u])
    {
        if(!dfn[v])//没被遍历过
        {
            tarjan(v,u);//就继续遍历
            low[u]=min(low[u],low[v]);
        }
        else if(vis[v]) low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u])
    {
        while(sta[top]!=u)
        {
            vis[sta[top]]=0;
            scc[sta[top]]=1;//标记这个节点是强连通分量
            top--;//弹栈
        }
        vis[u]=0;
        scc[u]=1;
    }
}

:::

好了，我们再来做道例题：

P1726 上白泽慧音

题面太长了，简单概括一下，就是让你求那些节点是强连通分量的大小，和里面的成员。

我们可以考虑记下如下信息：

• 有多少个强连通分量。
• 这个强连通分量的大小。

我们再按照大小排序，考虑建立 \(n\) 个优先队列（因为最多 \(n\) 个强连通分量）弹栈的时候，把这个节点的编号加到这个强连通分量里的优先队列，这样就自动排好序了。

:::success[Ac Code]

#include<bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define R register
#define rint register int
#define _ read<int>()
inline bool blank(const char x)
{
    return !(x^9)||!(x^13)||!(x^10)||!(x^32);
}
template<class T>inline T read()
{
    T r=0,f=1;R char c=gc();
    while(!isdigit(c))
    {
        if(c=='-') f=-1;
        c=gc();
    }
    while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
    return f*r;
}
inline void out(int x)
{
    if(x<0) pc('-'),x=-x;
    if(x<10) pc(x+'0');
    else out(x/10),pc(x%10+'0');
}
inline void read(char &x)
{
    for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=1e4+10;
struct oi
{
	int p,size;
    priority_queue<int,vector<int>,greater<int> >q;
}p[N];
vector<int>g[N];
int n,m,dfn[N],low[N],cnt,sta[N],top;
bitset<N>vis;
inline void sd(rint u)
{
	top--;
	vis[u]=0;
	p[cnt].p=cnt;//属于第几个强连通分量
	p[cnt].size++;//大小+1
	p[cnt].q.push(u);//节点加到优先队列里
}
inline void tarjan(rint u)
{
	dfn[u]=low[u]=++dfn[0];//dfn[0]是不会被遍历的我懒得在开一个变量所以就用dfn[0]
	sta[++top]=u;
    vis[u]=1;
	for(rint i=0;i<g[u].size();i++)
	{
		rint v=g[u][i];
		if(!dfn[v])
		{
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u])
	{
		cnt++;
		while(sta[top]!=u)
		{
			sd(sta[top]);
		}
		sd(u);
	}
}
inline bool cmp(oi x,oi y)
{
   	if(x.size!=y.size) return x.size>y.size;
	return x.q.top()<y.q.top();
}
signed main()
{
    n=_,m=_;
    for(rint i=1;i<=m;i++)
    {
        rint u=_,v=_,op=_;
        g[u].push_back(v);
        if(op==2) g[v].push_back(u);
    }
    for(rint i=1;i<=n;i++)
    {
        if(!dfn[i]) tarjan(i);//没被遍历过
    }
    sort(p+1,p+cnt+1,cmp);
    out(p[1].size);
    pc('\n');
    while(!p[1].q.empty())
    {
        out(p[1].q.top());
        p[1].q.pop();
        pc(' ');
    }
    return 0;
}

:::

P3387 【模板】缩点

题意大概就是给一张图，然后求出一条最长路。

注意到图中有环，所以我们可以考虑先把每个强连通分量缩成点（缩玩后的点的权值，是这个强连通分量里的节点之和），然后在缩完的 DAG 上跑 DP，求出最长路。

:::success[Ac Code]

#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long 
#define _ read<int>()
#define R register 
#define rint register int
template<class T>inline T read()
{
    R T r=0,f=1;R char c=gc();
    while(!isdigit(c))
    {
        if(c=='-') f=-1;
        c=gc();
    }
    while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
    return f*r;
}
inline void out(rint x)
{
    if(x<0) pc('-'),x=-x;
    if(x<10) pc(x+'0');
    else out(x/10),pc(x%10+'0');
}
const int N=1e4+10,M=1e5+10;
vector<int>g[N],e[N];
int a[N],dfn[N],low[N],sta[N],top,scc[N],u[M],v[M],n,m,in[N],dp[N];
bitset<N>vis;
inline void tarjan(rint u)
{   
    dfn[u]=low[u]=++dfn[0];
    sta[++top]=u,vis[u]=1;//入栈
    for(rint v:g[u])
    {
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(vis[v]) low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u])
    {
        do
        {
            vis[sta[top]]=0;
            scc[sta[top]]=u;
            if(sta[top]!=u) a[u]+=a[sta[top]];
        }
        while(sta[top--]!=u);
    }
}
inline void topp()
{
    for(rint i=1;i<=n;i++) g[i].clear();//先清空
    for(rint i=1;i<=m;i++)//建立新图
    {
        if(scc[u[i]]!=scc[v[i]])//不在一个强连通分量里
        {
            g[scc[u[i]]].push_back(scc[v[i]]);
            in[scc[v[i]]]++;
        }
    }
    queue<int>q;
    for(rint i=1;i<=n;i++)
    {
        if(scc[i]==i&&!in[i])//是一个强连通分量且入度为0
        {
            q.push(i);
            dp[i]=a[i];
        }
    }
    while(!q.empty())//拓扑
    {
        rint u=q.front();q.pop();
        for(rint v:g[u])
        {
            dp[v]=max(dp[v],dp[u]+a[v]);
            if(!(--in[v])) q.push(v);
        }
    }
}
signed main()
{
    n=_,m=_;
    for(rint i=1;i<=n;i++) a[i]=_;
    for(rint i=1;i<=m;i++)
    {
        u[i]=_,v[i]=_;
        g[u[i]].push_back(v[i]);
    }
    for(rint i=1;i<=n;i++)
    {
        if(!dfn[i]) tarjan(i);
    }
    topp();
    rint ans=0;
    for(rint i=1;i<=n;i++) ans=max(ans,dp[i]);
    out(ans);
    return 0;
}

:::

但是我还是建议你们手推一个简单的图，来模拟 tarjan 是怎么做的，但是为了不麻烦你我来带你们看看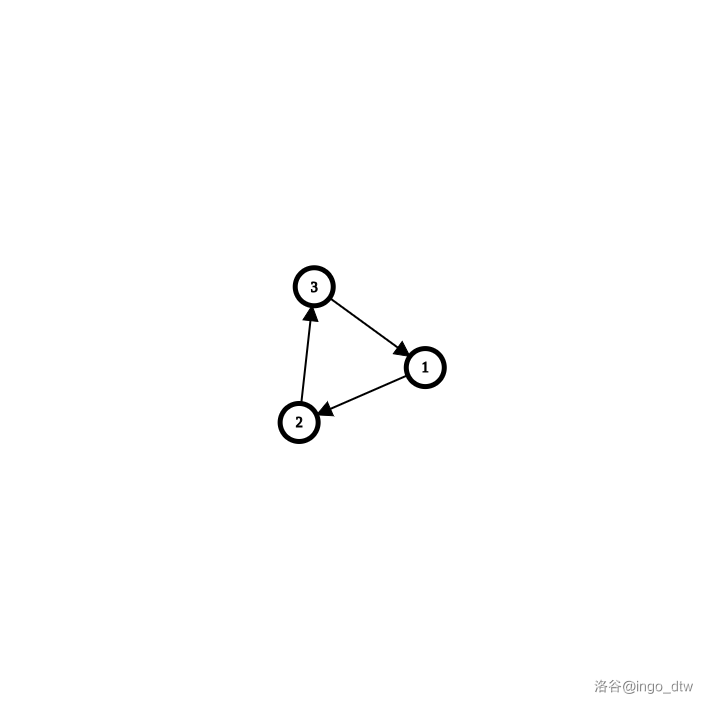：如图，这个图的强连通分量就是 \(1,2,3\)，那么 tarjan 是怎么做的呢？

遍历 \(1\) 的邻接节点 \(2\)，\(2\) 没有被搜过，先继续搜。

• 遍历 \(2\) 的邻接节点 \(3\)，\(3\) 没有被标记，继续搜。
  • 遍历 \(3\) 的邻接节点 \(1\)，\(1\) 被标记了，所以 \(low_3=dfn_1\)。
• 回到 \(2\)，\(low_2=low_3=1\)。

回到节点 \(1\)，\(low_1=low_2=low_3=1\)。

这个时候 \(low_1=dfn_1\)，所以我们开始弹栈，弹出的节点点 \(1,2,3\) 则为一个强连通分量。

2 割点与割桥

2.1 割点

其实割点的意思我通俗点来讲就是如果我们把一个图的某个点给删了，那么这个图不连通说明这个点是割点，割桥也差不多，就是把一个边给删了这个图不连通，说明这个边是割边。

虽然这个也是用 tarjan 求，但是这里面的 \(low\) 和求强连通分量的 \(low\) 定义是不一样的，\(dfn\) 都差不多。我们定义 \(low_u\) 为 \(u\) 这个节点不经过其父亲节点能到的节点的 \(dfn\) 的最小值。

那么我们判断一个点 \(u\) 是否是割点，的依据是有没有一个点 \(v\)（\(u\) 的邻接节点）使得 \(low_v \ge dfn_u\) 也就是无法通过一条回边（反祖边）到达 \(u\) 的祖先，你可以自己想象一下（这里建议画个图）。

但是这个其实是有反例的，你会发现这个点如果是你运行 tarjan 的起始点就不成立了，因为你无法回溯到 DFS 起始点之前的节点，但是如果这个点有 \(2\) 个子节点也是可以的，于是我们可以判一下在满足上面的条件同时不是父亲节点，或者满足条件子节点大于 \(1\)（因为你可以想象一下把一棵二叉树的根节点的两条边给拉开，图也是一样的（因为有 \(low_v \ge dfn_u\) 这个条件））。

:::success[Code]

inline void tarjan(rint u,rint fa)//记录一下父亲节点保证不是搜索开始的点
{
    dfn[u]=low[u]=++dfn[0];
    rint chd=0;
    for(rint v:g[u])
    {
        if(!dfn[v])
        {
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u])
            {
                chd++;
                if(u!=fa||chd>1) cut[u]=1;//是割点
            }
        }
        else low[u]=min(low[u],dfn[v]);
    }
}

:::

P3388 【模板】割点（割顶）

2.2 割边

我们再来看看割边，对于没有重边的时候我们判断割边的依据是 \(low_v > dfn_u\)（和上面一样）, 但是对于有重边那么这两条边都不可能是割边所以我们判断一下就好。

:::success[Code]

inline void tarjan(rint u,rint fa)
{
    dfn[u]=low[u]=++dfn[0];
    f[u]=fa;
    bool fl=0;
    for(rint v:g[u])
    {
        if(!dfn[v])
        {
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>dfn[u])
            {
                cut[u]=1;//u-v是割边
                ans++;
            }
        }
        else 
        {
            if(v!=fa||fl) low[u]=min(low[u],dfn[v]);
            else fl=1;
        }
    }
}

:::

为什么这样可以呢？因为我们用 \(fl\) 用来标记是否已经处理过一条从 \(u\) 指向父节点 \(fa\) 的回边。

当第一次遇到 \(v = fa\)（即回边指向父节点）时，\(fl\) 为假，于是走 else { flag = true; }，不执行 low[u] = min(low[u], dfn[v])。

之后如果再遇到 \(v = fa\)（说明有重边），此时 \(fl\) 为真，于是执行 low[u] = min(low[u], dfn[v])。

U623104 【模板】割边（桥）这是我自己造的题，你们做完后可以去看看 P1656 炸铁路 这道题。

3 双连通分量

好了，我们讲了割边和割点之后我们来看看怎么用 tarjan 求双连通分量。

对于点双连通，在一张连通的无向图中，如果 \(u\) 和 \(v\) 之间删掉任何点都不可以使得他们不连通（当然不能删掉 \(u\) 和 \(v\) 本身，而且只能删一个点），我们就称 \(u\) 和 \(v\) 点双连通。注意：点双连通不具有传递性。

对于边双连通，在一张连通的无向图中，如果删掉任意一条边都不能使得 \(u\)，\(v\) 不连通（只能删一条），我们就称 \(u\)，\(v\) 边双连通。注意：边双连通具有传递性。

然后边双连通分量就是一个无向图中最大的边双连通子图，点双连通同理。

要学双连通分量我们先了解 DFS 生成树，其实 DFS 生成树就是对一个图进行 DFS 的时候生成的一棵树，我们称在 DFS 生成树上的为树边，不在的为非树边。

根据 DFS 的性质，如果 \(u\) 和 \(v\) 之间用非树边连接，那么这两个点其中一个是另一个的祖先。

3.1 边双连通分量

边双连通分量 1

好了我们现在来看看怎么求割边，我们可以先把所有的桥给求出来，再 DFS 一遍，把所有边双连通分量给求出来。

P8436 【模板】边双连通分量

:::success[Code]

#include<bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define R register
#define rint register int
#define _ read<int>()
inline bool blank(const char x)
{
    return !(x^9)||!(x^13)||!(x^10)||!(x^32);
}
template<class T>inline T read()
{
    T r=0,f=1;R char c=gc();
    while(!isdigit(c))
    {
        if(c=='-') f=-1;
        c=gc();
    }
    while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
    return f*r;
}
inline void out(int x)
{
    if(x<0) pc('-'),x=-x;
    if(x<10) pc(x+'0');
    else out(x/10),pc(x%10+'0');
}
inline void read(char &x)
{
    for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=5e5+10;
vector<int>g[N],anss[N];
int dfn[N],low[N],f[N],ans,c[N];
bitset<N>cut;
inline void tarjan(rint u,rint fa)//求桥
{
    dfn[u]=low[u]=++dfn[0];
    f[u]=fa;
    bool fl=0;
    for(rint v:g[u])
    {
        if(!dfn[v])
        {
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
        }
        else 
        {
            if(v!=fa||fl) low[u]=min(low[u],dfn[v]);
            else fl=1;
        }
    }
}
inline void dfs(rint u,rint fa)
{
    c[u]=ans;
    if(u)
    {
        anss[ans].push_back(u);
    }
    for(rint v:g[u])
    {
        if(c[v]) continue;
        if((f[v]==u&&low[v]>dfn[u])||(f[u]==v&&low[u]>dfn[v])) continue;
        dfs(v,u);
    }
}
signed main()
{
    rint n=_,m=_;
    for(rint i=1;i<=m;i++)
    {
        rint u=_,v=_;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    for(rint i=1;i<=n;i++)
    {
        if(!dfn[i])
        {
            tarjan(i,0);
        }
    }
    for(rint i=1;i<=n;i++)
    {
        if(!c[i])
        {
            ans++;
            dfs(i,0);
        }
    }
    out(ans);
    pc('\n');
    for(rint i=1;i<=ans;i++)
    {
        out(anss[i].size());
        pc(' ');
        for(rint x:anss[i])
        {
            out(x);pc(' ');
        }
        pc('\n');
    }
    return 0;
}

:::

边双连通分量 2

但是我突然就不想写 DFS 怎么办？我们回忆一下最开始求强连通分量的时候，我们看看可不可以用栈来避免写这个 DFS，于是你会发现，其实无向图求边双连通分量就是在有向图求强连通分量（你也可以理解为在有向图中求强连通分量，但需要注意无向图的特殊性）。

:::success[Code]

#include<bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define R register
#define rint register int
#define _ read<int>()
inline bool blank(const char x)
{
    return !(x^9)||!(x^13)||!(x^10)||!(x^32);
}
template<class T>inline T read()
{
    T r=0,f=1;R char c=gc();
    while(!isdigit(c))
    {
        if(c=='-') f=-1;
        c=gc();
    }
    while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
    return f*r;
}
inline void out(int x)
{
    if(x<0) pc('-'),x=-x;
    if(x<10) pc(x+'0');
    else out(x/10),pc(x%10+'0');
}
inline void read(char &x)
{
    for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=5e5+10;
vector<int>g[N],anss[N];
int dfn[N],low[N],f[N],ans,c[N],sta[N],top;
bitset<N>cut;
inline void tarjan(rint u,rint fa)//求桥
{
    dfn[u]=low[u]=++dfn[0];
    f[u]=fa;
    sta[++top]=u;
    bool fl=0;
    for(rint v:g[u])
    {
        if(!dfn[v])
        {
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
        }
        else 
        {
            if(v!=fa||fl) low[u]=min(low[u],dfn[v]);
            else fl=1;
        }
    }
    if(low[u]==dfn[u])
    {
        ans++;
        while(1)
        {
            rint x=sta[top--];
            c[x]=ans;
            anss[ans].push_back(x);
            if(x==u) break;
        }
    }
}
signed main()
{
    rint n=_,m=_;
    for(rint i=1;i<=m;i++)
    {
        rint u=_,v=_;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    for(rint i=1;i<=n;i++)
    {
        if(!dfn[i])
        {
            tarjan(i,0);
        }
    }
    out(ans);
    pc('\n');
    for(rint i=1;i<=ans;i++)
    {
        out(anss[i].size());
        pc(' ');
        for(rint x:anss[i])
        {
            out(x);pc(' ');
        }
        pc('\n');
    }
    return 0;
}

:::

3.2 点双连通分量

我们先说个性质：

• 两个点双连通分量最多一个公共点，这个点一定是割点。

于是我们考虑在求割点的时候用栈记录一下之前的点最后如果遇到个点就开始弹栈，代码如下（我这里用的点栈，据说用边栈更好）：

:::success[Code]

#include <bits/stdc++.h>
using namespace std;
#ifdef __linux__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#define int long long
#define _ read<int>()
#define rint register int
#define R register
inline bool blank(const char &x)
{
    return !(x^10)||!(x^9)||!(x^13)||!(x^32);
}
template<class T>inline T read()
{
    T r=0,f=1;R char c=gc();
    while(!isdigit(c))
    {
        if(c=='-') f=-1;
        c=gc();
    }
    while(isdigit(c)) r=(r<<1)+(r<<3)+(c^48),c=gc();
    return f*r;
}
inline void out(rint x)
{
    if(x<0) pc('-'),x=-x;
    if(x<10) pc(x+'0');
    else out(x/10),pc(x%10+'0');
}
inline void read(char &x)
{
    for(x=gc();blank(x)&&(x^-1);x=gc());
}
const int N=5e5+10;
vector<int>g[N],anss[N];
bitset<N>cut;
int dfn[N],low[N],ans,sta[N],top;
inline void tarjan(rint u,rint fa)//记录一下父亲节点保证不是搜索开始的点
{
    dfn[u]=low[u]=++dfn[0];
    rint chd=0;
    sta[++top]=u;
    if(u==fa&&g[u].empty())//孤立点处理
    {
        anss[++ans].push_back(u);
        top--;
        return;
    }
    for(rint v:g[u])
    {
        if(v==fa) continue;//跳过父亲
        if(!dfn[v])
        {
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u])
            {
                chd++;
                if(u!=fa||chd>1) cut[u]=1;//是割点
                rint x;
                ans++;
                anss[ans].push_back(u);
                do
                {
                    x=sta[top--];
                    anss[ans].push_back(x);
                }while(x!=v);
            }
        }
        else low[u]=min(low[u],dfn[v]);
    }
}
signed main()
{
    rint n=_,m=_;
    for(rint i=1;i<=m;i++)
    {
        rint u=_,v=_;
        if(u==v) continue;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    for(rint i=1;i<=n;i++)
    {
        if(!dfn[i])
        {
            top=0;
            tarjan(i,i);
        }
    }
    out(ans);
    pc('\n');
    for(rint i=1;i<=ans;i++)
    {
        out(anss[i].size());pc(' ');
        for(rint x:anss[i])
        {
            out(x);pc(' ');
        }
        pc('\n');
    }
    return 0;
}

:::

P8435 【模板】点双连通分量

4 结尾

总而言之 tarjan 最重要的就是 \(low\)，\(dfn\) 这两个东西，无论是强连通分量、割点与割桥、双连通分量本质都是根据 \(dfn\) 和 \(low\) 的关系，找到图中的“核心关联结构”。如果你搞懂了这些 tarjan 对你来说已经不算太难啦。

记住机房大佬的那句话：DAG 为什么没有环。 而现在，我们已经学会了如何找出图中所有的环！

5 upd

\(1\)：感谢@HHC883 指出我的错误。

\(2\)：感谢@HoLuc1078 指出图例问题，与写法问题。

如果还有错误或疑问，欢迎私信我！