#15 3Sum

#15 3Sum

问题描述

Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.

Given array nums = [-1, 0, 1, 2, -1, -4],

A solution set is:
[
[-1, 0, 1],
[-1, -1, 2]
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/3sum

解题思路

俗话说磨刀不误砍柴工，如果直接暴力求解的话，时间复杂度为\(O(n^3)\)。所以我们先将其进行排序，时间复杂度为\(O(logn)\)。然后在考虑如何求解。

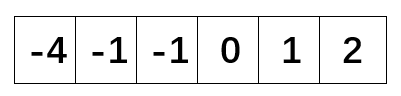
这里我们的思路是利用双指针法，对每一个元素进行遍历。

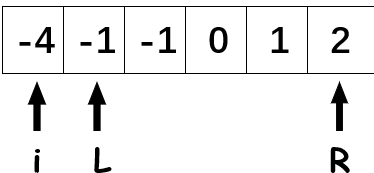
这里我们设置两个指针：左指针\(L\)和右指针\(R\)。通过指针的移动判断此时三个数字之和是否为0。

由于我们已经对数组进行排序，所以若三数之和小于0，则左指针向右移动；若三数之和大于0，则右指针向左移动。

这里我们判断\(-4-1+2<0\)，那么\(L\)向右移动。

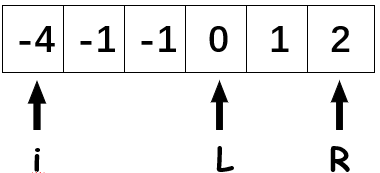
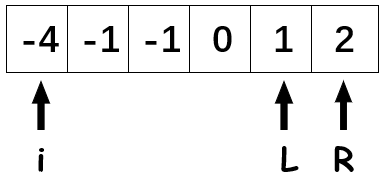
重复此过程，直至\(L\)与\(R\)相遇，开始下一次循环，指针\(i\)向右移动，重置\(L\)和\(R\)指针。（由于不允许找到重复的组合，所以当指针\(i\)向右不断移动，直到该值与前一项不同。）

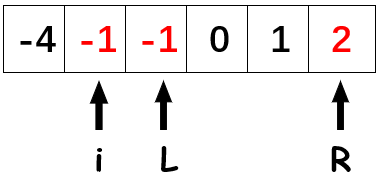
此时我们找到符合结果的组合，将其记录下来并移动\(L\)和\(R\)指针，直至二者相遇。

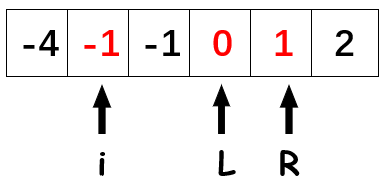
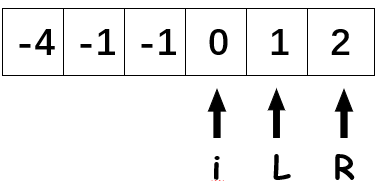
遍历结束，我们即可得到不重复且符合规定的组合。

时间复杂度：\(O(n^2)\)，外循环\(i\)指针遍历，内循环\(L,R\)指针遍历，\(O(n)*O(n)\)。

空间复杂度：\(O(n)\)，使用常数大小的空间存放指针。

代码解释

line 11~18:若数组长度小于等于3，可直接判断

line 22~23:\(i\)指针移动时忽略重复值

line 24~25:若当前\(i\)指针指向大于0的数，那么三数之和必大于0（已经排序），可直接退出遍历

line 29~42：判断三数之和并且移动相应的指针。这里有个小trick，对于line 29和line 32，在指针移动时无需判断是否与前一项重复（因为就算重复了也不满足三数之和为0），所以可直接用line 28的while循环；但是如果满足条件，即line 36，那么在移动指针时须注意跳过重复项。

Github