【软工】第一次个人项目——数独
一、项目源码的github链接
https://github.com/wz111/sudoku_onlycode
(因为使用github不熟练-_-,在sudoku仓库关联了项目文件夹,导致大小接近100M。因此新开sudoku_onlycode仓库来最终提交。为保留提交历史,sudoku仓库未删除)
二、需求分析
- 生成数独
命令:
sudoku.exe -c n
要求:
1.输出到sudoku.txt
2.生成的数独不重复
3.1<=n<=1000000,支持前置零以及前置加号,不支持运算式
4.可以处理异常情况,如:sudoku.exe -c abc
5.左上角第一个数为(学号后两位相加)% 9 + 1=(8+9)%9+1=9
6.参数不合法输出异常信息到控制台- 求解数独
命令:
sudoku.exe -s absolute_path_of_puzzlefile
要求:
1.输出到sudoku.txt
2.数独中的0代表空格
3.文件中数独题目数为n,1<=n<=1000000
4.保证格式正确
5.对每个数独题目求出一个可行解
6.参数不合法输出异常信息到控制台
三、解题思路
刚拿到项目时,自然地将其分为生成终局和求解数独两部分。
生成终局
开始时对生成终局没什么思路,通过查阅资料找到这样一篇博文,由博主的方法以及和室友们的热烈讨论,发现可以生成1-9中八个数的全排列,暂且将其定义为种子数组,用数组索引替换的形式,将一个已知数独变换成另外8!-1个不同的数独,因为[0,0]元素确定,所以是8!-1。这样距离我们要求的1000000个数独还有很大差距,还是经过查阅资料后,找到了一篇博文,其中介绍了基于矩阵变换的数独生成方法,这里我只采用了行变换的思路,需要保证的是:交换只发生在前三行,中间三行,最后三行之间。而不能越界交换,比如第一行和第四行交换就是不允许的。但是这种方式随机性较差,而且每次运行程序的原始矩阵都相同,所以我进行了一些改进: 在进行索引替换前,对原始的种子数组进行一次索引替换,生成一个初始种子,用这个初始种子对祖先数独进行索引替换得到初始数独。对这个初始数独进行索引变换加行变换。这样可以保证每次开始的初始数独不一样。
求解数独
暴力回溯的想法很成熟,但是还是比较关心有没有更好的方法,依然是查阅资料后,找到了DLX算法,即将问题转化为精确覆盖问题求解。但是考虑到自己的水平不高,实现了DLX可能没有时间进行充分的优化,而未优化的DLX会比暴力慢好多。思前想后还是决定写暴力。。。在空白格的表示方法以及去除候选数的方法上,参照了这篇博文。主要想法是将数字用类似二进制的方式表示,即1=000000001,2=000000010,……, 9=100000000, 0=111111111,即每一位代表这个位置取值的可能性。取出一个数字可能性可以用取反做位与的方式,例如这个空白位置不能取2,则有111111111 & (111111101)=111111101,这样就去除了2的可能。
四、设计实现过程
我使用了两个类来进行数据的组织以及方法的实现。现详细说明:
EndProducer类
- private属性:
int _ancestorMartix[81]: 祖先数独
int _originalMartix[81]: 原始数独
int _seed[9]: 原始种子数组
int _initialSeed[9]: 初始种子数组
int Nums: 要生成的数独数量
- public方法:
void Swap(int* a, int* b):交换方法
int* ROWijk(int* a):行变换方法(i,j,k的排列方式代表交换方式),传入的是数独数组首地址,返回的是交换后的数组地址。
int* getInitialSeed():得到随机的初始种子
bool DuplicateCheck(int* a, int aim, int count):重复性检查方法。检查地址为a的数组中是否存在aim元素,count表示当前的数组长度。
bool IndexSubstitution(int* seed, int* a, int* b, int len):索引替换方法。对长度为len的a数组进行以seed为种子的索引替换得到b。
void MainOperation():主操作方法。生成数独。
SolveSudoku类
- private属性:
int _puzzle[81]:数独谜题
int _flag[81]:标记数组,如果这个位置的数是唯一的,那么相应的标记数组位置为1,否则为0.
- public方法:
void setPuzzle(int a[]):顾名思义,将_puzzle赋值为a
int* getPuzzle():返回_puzzle的副本
void setFlag(int a[]):顾名思义,将_flag赋值为a
int NumTranfor(int a):将a转换成用到的数字。
int RemoveCandidates(int index):去掉index位置的不合要求的候选数
bool Fill(int index):在index位置填数
流程图
输入参数为'-c':
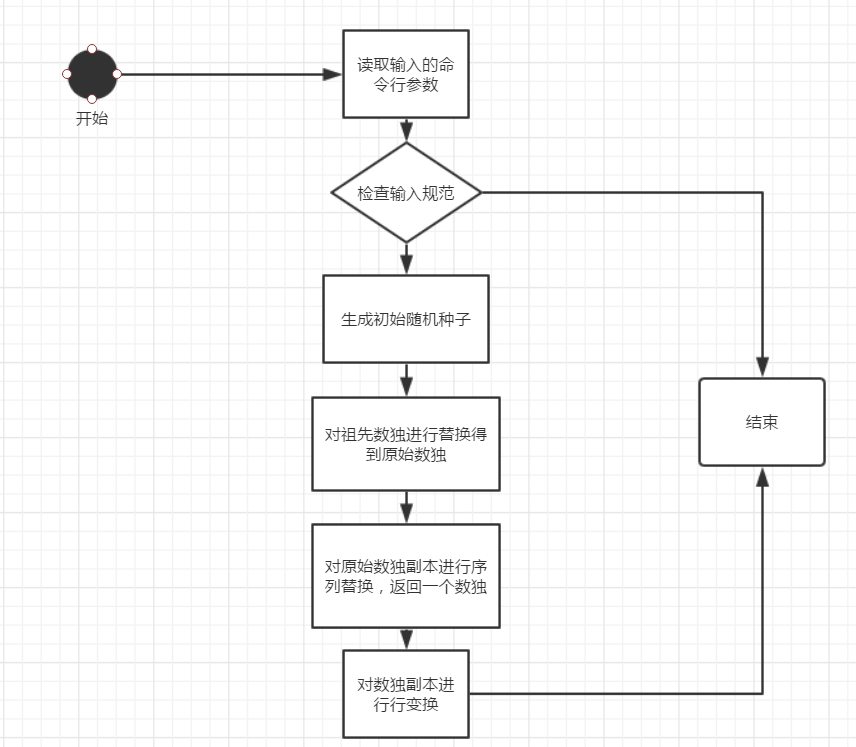
输入参数为‘-s’:
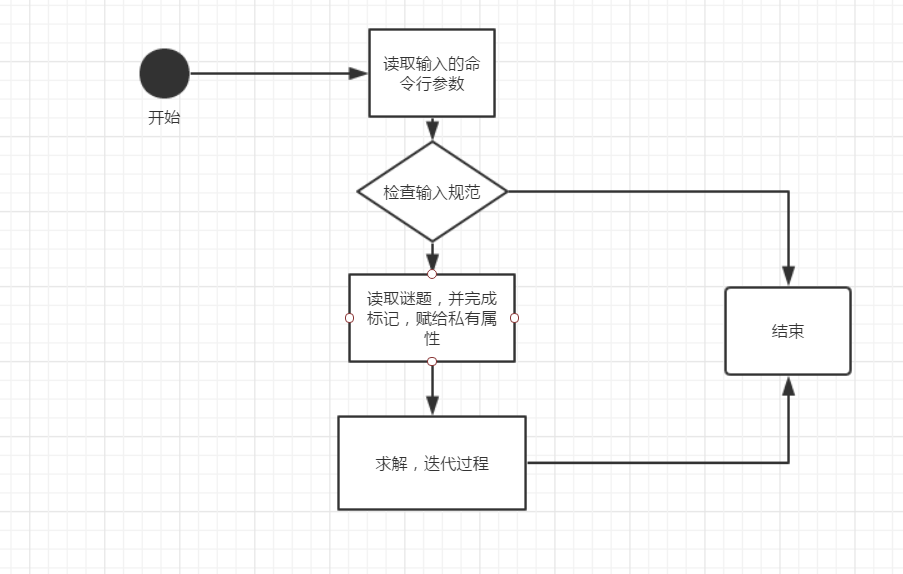
单元测试设计
TEST_METHOD(End_Test_ROW987)
{
EndProducer EP(12);
int arr[81] = { 0 };
memset(arr + 54, 7, sizeof(int) * 9);
memset(arr + 63, 8, sizeof(int) * 9);
memset(arr + 72, 9, sizeof(int) * 9);
int Real[81] = { 0 };
memcpy(Real, EP.Row987(arr), sizeof(int) * 81);
memset(arr + 54, 7, sizeof(int) * 9);
memset(arr + 63, 8, sizeof(int) * 9);
memset(arr + 72, 9, sizeof(int) * 9);
for (int i = 54; i < 63; i++) {
Assert::AreEqual(Real[i], arr[i + 18]);
Assert::AreEqual(Real[i + 9], arr[i + 9]);
Assert::AreEqual(Real[i + 18], arr[i]);
}
}
TEST_METHOD(End_Test_DuplicateCheck)
{
EndProducer es(12);
int arr[10] = { 1,2,3,4,5,5,5,3,2,0 };
int x = 6;
int y = 1;
int Count = 9;
bool expect_in = es.DuplicateCheck(arr, y, Count);
bool expect_out = es.DuplicateCheck(arr, x, Count);
Assert::AreEqual(expect_in, true);
Assert::AreEqual(expect_out, false);
}
TEST_METHOD(End_Test_getInitialSeed)
{
EndProducer ep(12);
int arr[9] = { 1,2,3,4,5,6,7,8,9 };
int* arr1 = NULL;
arr1 = ep.getInitialSeed();
for (int i = 0; i < 9; i++) {
Assert::AreNotEqual(*(arr1 + i), arr[i]);
}
}
TEST_METHOD(End_Test_IndexIndexSubstitution)
{
EndProducer ep(12);
int arr1[9] = { 4,6,3,2,1,8,9,5,7 };
int test_seed[9] = { 9,2,4,6,5,1,7,8,3 };
int arr2[9] = { 0 };
ep.IndexSubstitution(test_seed, arr1, arr2, 9);
int expect_arr2[9] = { 6,1,4,2,9,8,3,5,7 };
for (int i = 0; i < 9; i++) {
Assert::AreEqual(arr2[i], expect_arr2[i]);
}
}
TEST_METHOD(Sol_Test_setPuzzle)
{
SolveSudoku test_ss;
int x[81] = { 0 };
x[1] = 9;
x[5] = 1;
x[4] = 2;
test_ss.setPuzzle(x);
int* y = test_ss.getPuzzle();
Assert::AreEqual(x[1], y[1]);
Assert::AreEqual(x[4], y[4]);
Assert::AreEqual(x[5], y[5]);
}
TEST_METHOD(Sol_Test_NumTransfor)
{
SolveSudoku test_ss;
int x1 = 1;
int x2 = 4;
int x3 = 9;
Assert::AreEqual(test_ss.NumTransfor(x1), 0x1);
Assert::AreEqual(test_ss.NumTransfor(x2), 0x8);
Assert::AreEqual(test_ss.NumTransfor(x3), 0x100);
}
关于单元测试,我是对每个类中的每个方法单独进行了进行了测试,具体代码可参看顶部的github链接。
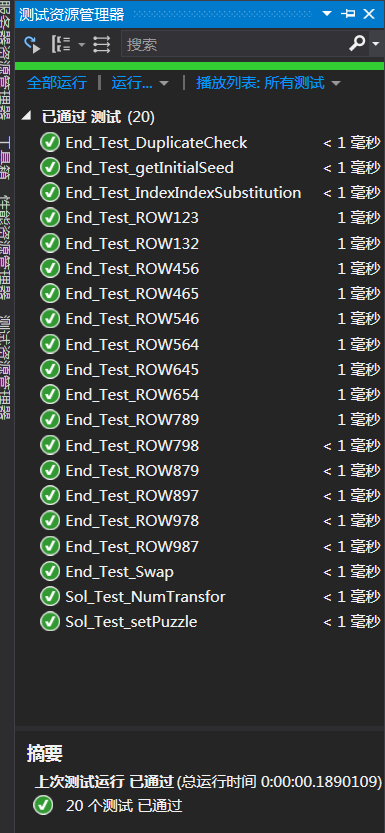
覆盖率
这是参数为‘-c’时EndProducer类的覆盖率:

这是参数为‘-s’时SolveSudoku类的覆盖率:

五、性能分析
最开始的版本生成1000000个数独需要263秒左右的时间,启动性能分析,查看生成数独部分的调用关系树
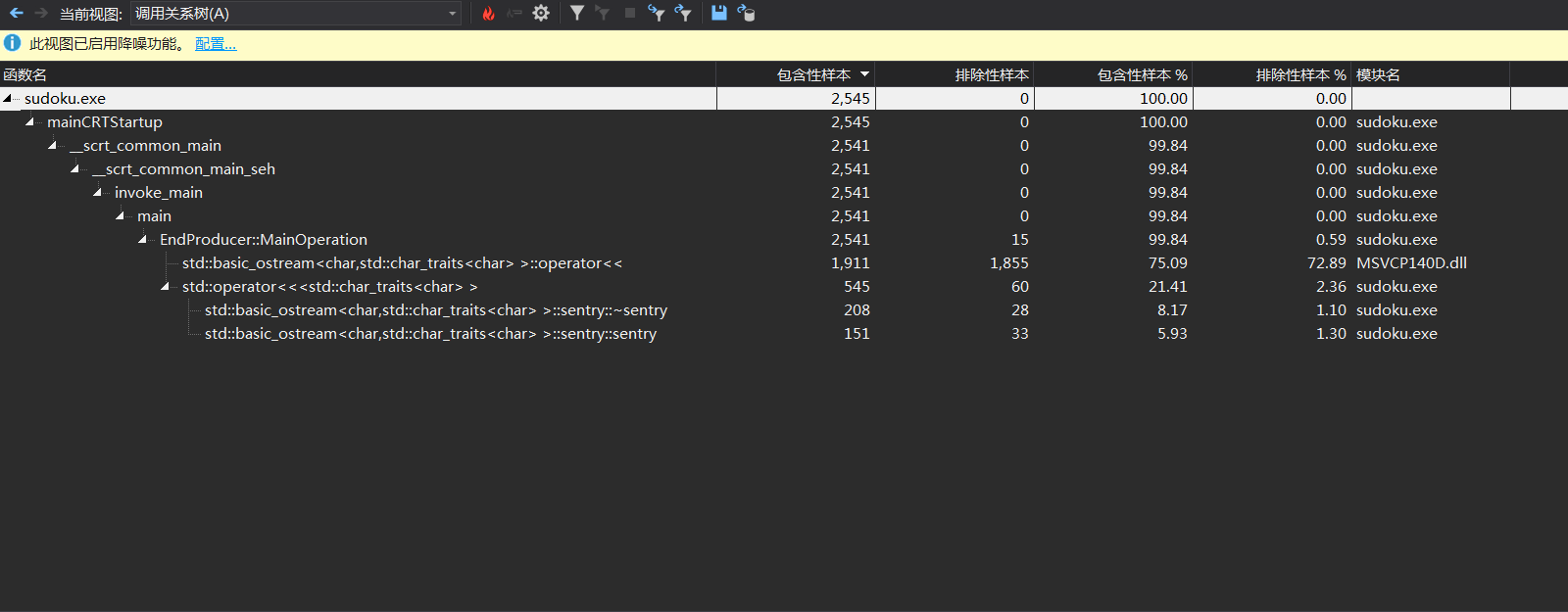
发现开销最大的函数是这个out<<,找到这部分的代码,发现我们是每次向文件中输出一个字符,又因为c++中IO会占用较长时间
因此改用fputs,一次输出一个终盘。修改后的时间达到了3.76s。
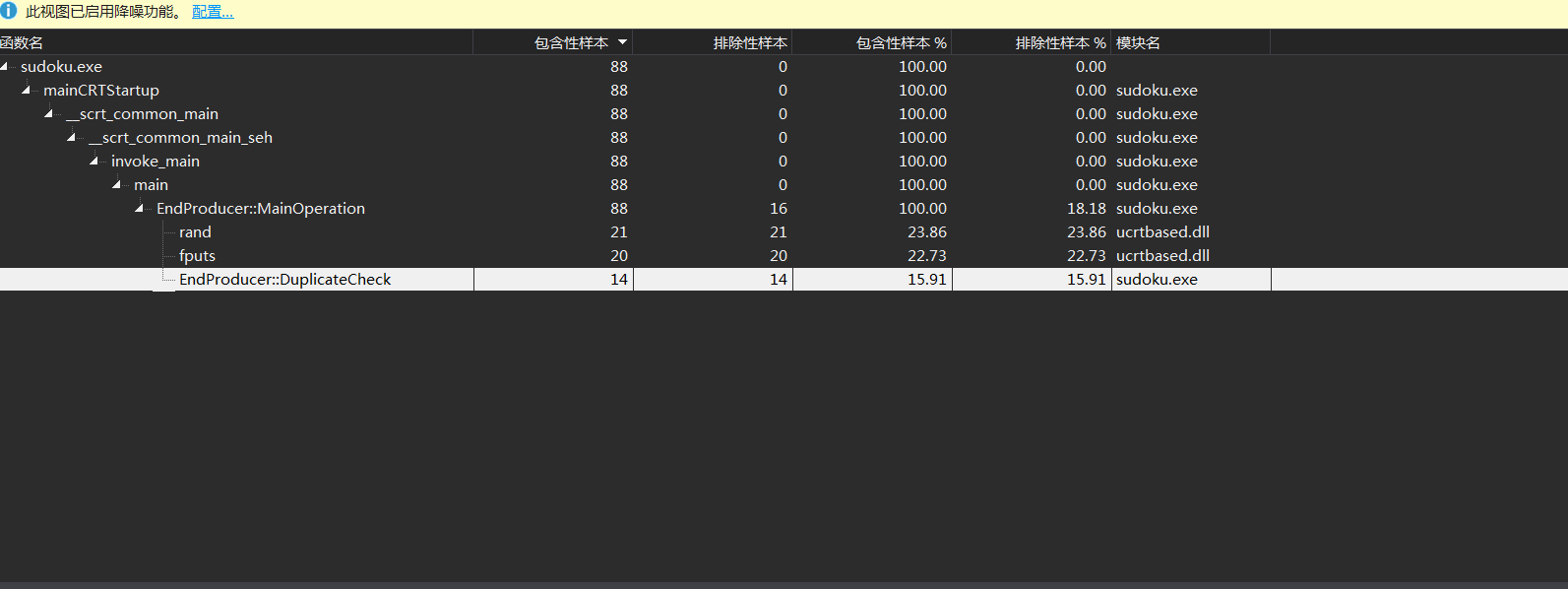
解题方面,性能分析发现开销最大的函数是Fill(int index),意料之中。而且RemoveCandidates方法以及NumTransfor方法均在Fill中被调用,才造成开销大的问题。
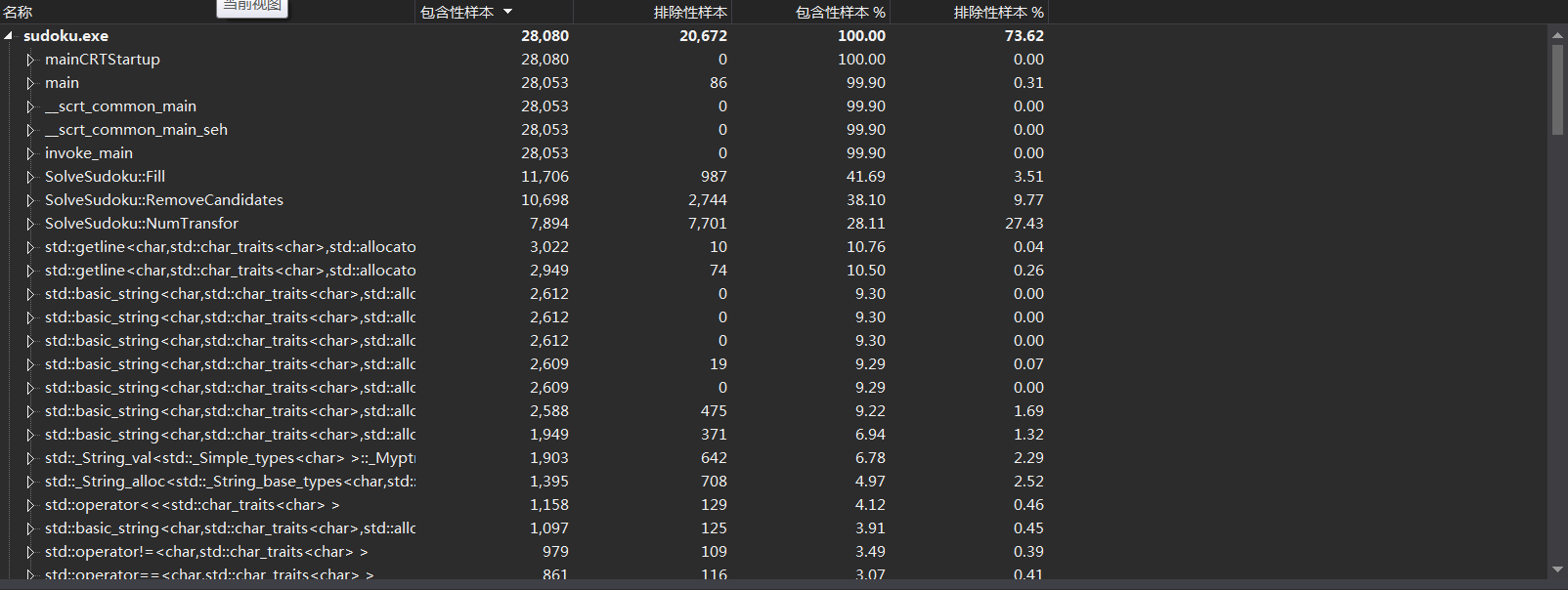
六、代码分析
行变换函数,仅以978变换为例
int* EndProducer::Row978(int* a)
{
int top = (7 - 1)*NUM_ROW;
int end = (9 - 1)*NUM_ROW;
for (int i = 0; i < NUM_ROW; i++) {
Swap(&a[top + i], &a[end + i]);
}
top = (8 - 1)*NUM_ROW;
end = (9 - 1)*NUM_ROW;
for (int i = 0; i < NUM_ROW; i++) {
Swap(&a[top + i], &a[end + i]);
}
return a;
}
索引替换方法
void EndProducer::IndexSubstitution(int* seed, int* a, int* b, int len)
{
int i;
//int result[81] = { 0 };
for( i = 0 ; i < len ; i++ )
{
int temp = a[i];
b[i] = seed[temp - 1];
}
}
谜题数字转换,其中NUM1~NUM9均在头文件中定义
int SolveSudoku::NumTransfor(int a)
{
int temp = 0;
switch (a)
{
case 1:
temp = NUM1;
break;
case 2:
temp = NUM2;
break;
case 3:
temp = NUM3;
break;
case 4:
temp = NUM4;
break;
case 5:
temp = NUM5;
break;
case 6:
temp = NUM6;
break;
case 7:
temp = NUM7;
break;
case 8:
temp = NUM8;
break;
case 9:
temp = NUM9;
break;
default:
cout << "Error4" << endl;
exit(1);
break;
}
return temp;
}
去除index位置中不符合要求的候选数。
int SolveSudoku::RemoveCandidates(int index)
{
if (_flag[index] == 1)
{
return _puzzle[index];
}
int row = index / 9;
int col = index % 9;
int m = row / 3;
int n = col / 3;
int i1;
int j1;
int pointCopy = _puzzle[index];
//Palace candidates removal
for (i1 = m * 3; i1 < m * 3 + 3; i1++)
{
for (j1 = n * 3; j1 < n * 3 + 3; j1++)
{
if (_flag[i1 * 9 + j1] == 1)
{
pointCopy = pointCopy & (~NumTransfor(_puzzle[i1 * 9 + j1]));
}
}
}
//row and col candidates removal
int i;
for (i = 0; i < 9; i++)
{
if (_flag[row * 9 + i] == 1)
{
pointCopy = pointCopy & (~NumTransfor(_puzzle[row * 9 + i]));
}
if(_flag[i * 9 + col] == 1)
{
pointCopy = pointCopy & (~NumTransfor(_puzzle[i * 9 + col]));
}
else
;
}
return pointCopy;
}
回溯求解数独的Fill方法
bool SolveSudoku::Fill(int index)
{
if (index >= 81)
{
return true;
}
int shiftvalue = RemoveCandidates(index);
int pointCopy = _puzzle[index];
if(_flag[index] == 0)
{
for (int i = 1 ; shiftvalue > 0 ; i++)
{
if (shiftvalue % 2 != 0)
{
_puzzle[index] = i;
_flag[index] = 1;
if (Fill(index + 1))
{
return true;
}
}
shiftvalue = shiftvalue >> 1;
}
}
else
{
return Fill(index + 1);
}
_puzzle[index] = pointCopy;
_flag[index] = 0;
return false;
}
七、PSP图

八、总结
这次作业应该是我第一次文档指挥编码的作业,结果还是不太成功,实现过程中还是出现了该文档的问题,由此暴露出的问题有几个。
一个是对C++不熟悉,以至于编码前先去看了几节C++面向对象的网课,但感觉效果不好,还不如在编码过程中学到的多。
还有就是这次太重视设计了,以至于有时候想的偏离了正确轨道,意识到的时候发现和项目好像没啥关系。
最后还是C的基础不扎实,经常会写着写着去查百度,很多知识没有熟练掌握,这大幅增加了编码时间。
2017.9.29修改
-
将Rowjik方法进行了整合,修改为RowSwap函数,github已更新。主要思路为将目标序列与升序序列比较,若相对位置不同,则替换两者所对应行,同时替换两者位置,直到与升序序列相等时停止。
-
今天看到作业结果居然生成了重复的终局,心态炸穿,在EndProducer.cpp中的MainOperation函数中发现了问题,是个老生常谈的错误了,因为我的行变换函数是直接修改地址,因此在对原始矩阵进行变换的时候要保留一个副本,我想到了这个问题,实现的时候却犯了想当然的错误!我新建了一个int* OriMartixCopy来保留副本,同时新建了一个int* OriMarRowCopy来用于行变换,结果在赋值时直接写成了:
OriMarRowCopy = OriMartixCopy;
相当于将两个指针同时指向原数组,失去了原本的意义。现在改为:
for(int i = 0 ; i < 81 ; i++)
{
OriMarRowCopy[i] = OriMartixCopy[i];
}
相应的,单元测试也进行了修改。但是在解题时居然会题目与解的数目不一,有些费解,以后再查。
- 这个问题也已经找到,还是对C++流处理的理解不够,写入出现问题:
fstream outfile("sudoku.txt");
初步试验后发现,写成ofstream就可以,
ofstream outfile("sudoku.txt");
查阅了C++ Reference关于fstream和ofstream的内容后发现,fstream有一个成员常数out,这个out会使内部缓冲流支持文件写入操作,而在ofstream中,这个out是默认设置的。所以ofstream可以而fstream不行,也可以在构造时对fstream进行手动添加成员常量out,即:
fstream outfile("sudoku.txt", std::fstream::out);
总结一下,还是懒,其实花少量的时间写一个测试程序就可以解决的。这次就引以为戒,在结对项目中绝对绝对不能这么马虎了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号