图(基于十字链表)实现
1.Gragh抽象类 (gragh.h):
#ifndef _GRAGH_H
#define _GRAGH_H
template <typename E> //E为标号的类型
class Graph{
public:
Graph() {} //构造函数
virtual ~Graph() {} //析构
//返回顶点和边的数量
virtual int n() = 0; //顶点
virtual int e() = 0; //边
//返回v的第一个相邻顶点的下标
virtual int firstOut(int v) = 0; //出边
virtual int firstIn(int v) = 0; //入边
//返回v的下一个相邻顶点的下标
virtual int nextOut(int v) = 0;
virtual int nextIn(int v) = 0;
//查找,设置,获取顶点的标号
virtual int locateVex(E u) =0; //查找标号
virtual E getVex(int v)=0;
virtual void putVex(int v,E value) =0;
//建立,删除边,获取边的权值
virtual void setEdge(int v1,int v2,int wght) = 0;
virtual void delEdge(int v1,int v2) = 0;
virtual int weight(int v1, int v2) =0;
//设置,获取标记
virtual int getMark(int v) =0;
virtual void setMark(int v, int value) =0;
};
#endif
2.边类 (edge.h):
#ifndef _EDGE_H
#define _EDGE_H
class Edge //边类
{
private:
int tailnum,headnum;//弧头弧尾的下标
int _weight; //权值
Edge *tailp; //指向tail相同的下一条边
Edge *headp; //指向head相同的下一条边
public:
Edge(int tl,int hd,Edge *t0p,Edge *hp,int wgt=1)
{
tailnum=tl;
headnum=hd;
tailp=t0p;
headp=hp;
_weight=wgt;
}
void setWeight(int wgt) { _weight=wgt; } //更改权值
void setTailp(Edge *t0p) { tailp=t0p; } //重设tail的下一条出边
void setHeadp(Edge *hp) { headp=hp; } //重设head的下一条入边
int weight() { return _weight; } //返回权值
int tail() { return tailnum; } //返回弧尾
int head() { return headnum; } //返回弧头
Edge* tailNext() { return tailp; } //弧尾的下一条出边
Edge* headNext() { return headp; } //弧头的下一条入边
};
#endif
3.顶点类 (vexnode.h)
#ifndef _VEXNODE_H
#define _VEXNODE_H
template <typename E> //顶点类
class VexNode
{
public:
E vex; //标号
Edge *outedge; //储存出边
Edge *inedge; //储存入边
VexNode()
{
outedge=inedge=NULL;
}
};
#endif
4.图类 (OLgragh.h)
#ifndef _OLGRAGH_H
#define _OLGRAGH_H
#include"gragh.h"
#include"edge.h"
#include"vexnode.h"
template <typename E>
class OLGragh : public Graph<E> //十字链表实现
{
private:
int numVertex,numEdge; //顶点和边的数量
VexNode<E> *vexarray; //顶点数组
int *mark; //标记数组
Edge **outCurr; //保存出边链表的当前位置
Edge **inCurr; //保存入边链表的当前位置
void Init(int n) //初始化一个含n个顶点的图
{ //由于顶点标号类型不确定,故未初始化顶点数组,请根据标号类型手动初始化顶点数组
numEdge=0;
numVertex=n;
outCurr = new Edge* [n];
inCurr = new Edge* [n];
mark = new int[n];
vexarray = new VexNode<E>[n];
for(int i=0;i<n;i++)
{
mark[i]=0;
inCurr[i]=outCurr[i]=NULL;
}
}
public:
OLGragh(int n) { Init(n); }
~OLGragh()
{
delete [] mark;
delete [] outCurr;
delete [] inCurr;
for(int i=0;i<numVertex;i++)
{
Edge *next=vexarray[i].outedge;
Edge *curr=NULL;
while(next != NULL)
{
curr=next;
next=curr->tailNext();
delete curr;
}
delete curr;
}
delete [] vexarray;
}
//返回顶点和边的数量
int n(){ return numVertex; }
int e(){ return numEdge; }
//返回v的第一个出边相邻顶点
int firstOut(int v)
{
outCurr[v] = vexarray[v].outedge;
if(outCurr[v])
return outCurr[v]->head() ;
return -1; //无边的情况
}
//返回v的下一个出边相邻顶点
int nextOut(int v)
{
if(!outCurr[v])
return -1;
outCurr[v]=outCurr[v]->tailNext();
if(outCurr[v])
return outCurr[v]->head();
return -1; //已经是最后一个顶点
}
//返回v的第一个入边相邻顶点
int firstIn(int v)
{
inCurr[v]=vexarray[v].inedge;
if(inCurr[v])
return inCurr[v]->tail();
return -1; //无边的情况
}
//返回v的下一个入边相邻顶点
int nextIn(int v)
{
if(!inCurr[v])
return -1;
inCurr[v]=inCurr[v]->headNext();
if(inCurr[v])
return inCurr[v]->tail();
return -1; //已经是最后一个顶点
}
int locateVex(E u) //查找标号
{
int i;
for(i=0;i<numVertex;i++)
{
if(vexarray[i].vex == u) return i;
}
return -1; //查找失败的情况
}
E getVex(int v) //返回标号
{
return vexarray[v].vex;
}
void putVex(int v,E value) //设置标号
{
vexarray[v].vex=value;
}
//建立,删除边
void setEdge(int v1,int v2,int wght=1)
{
vexarray[v1].outedge=vexarray[v2].inedge=new Edge(v1,v2,vexarray[v1].outedge,vexarray[v2].inedge,wght);
numEdge++;
}
void delEdge(int v1,int v2) //删除边后对应顶点的tmp指针失效,next函数不能返回正确的结果,应重新使用first
{
outCurr[v1]=inCurr[v2]=NULL; //防止出现野指针
Edge *del=NULL;
Edge *curr=NULL;
Edge *next=vexarray[v1].outedge;
while(next != NULL) //从v1的边中删除
{
if(next->head()==v2)
{
del=next;
if(curr==NULL) //<v1,v2>是v1的第一条出边的情况
vexarray[v1].outedge=del->tailNext();
else
curr->setTailp(del->tailNext());
}
curr=next;
next=curr->tailNext();
}
curr=NULL;
next=vexarray[v2].inedge;
while(next != NULL) //从v2的边中删除
{
if(next->tail()==v1)
{
del=next;
if(curr==NULL) //<v1,v2>是v2的第一条入边的情况
vexarray[v2].inedge=del->headNext();
else
curr->setHeadp(del->headNext());
}
curr=next;
next=curr->headNext();
}
if(del != NULL)
numEdge--;
delete del;
}
int weight(int v1, int v2) //获取给定边的权值
{
Edge *curr=vexarray[v1].outedge;
while(curr!=NULL)
{
if(curr->head() == v2)
return curr->weight();
curr=curr->tailNext();
}
return 0;
}
virtual int getMark(int v) //获取标记
{
return mark[v];
}
virtual void setMark(int v, int value) //设置标记
{
mark[v]=value;
}
};
#endif
5.测试程序(OLgragh.cpp)
#include<iostream>
#include"gragh.h"
#include"OLgragh.h"
using namespace std;
//dfs:打印顶点标号和所有出,入边的权之和
void DFS(int v1,OLGragh<char> &G)
{
if(G.getMark(v1))
return ;
G.setMark(v1,1);
int s1,s2;
s1=s2=0;
int p=G.firstOut(v1);
while(p!=-1)
{
s1+=G.weight(v1,p);
p=G.nextOut(v1);
}
p=G.firstIn(v1);
while(p!=-1)
{
s2+=G.weight(p,v1);
p=G.nextIn(v1);
}
cout << G.getVex(v1)<<"的出边权之和(无权图的出度):"<<s1
<<" 入边权之和(无权图的入度):"<<s2<<endl;
p=G.firstOut(v1);
while(p!=-1)
{
DFS(p,G);
p=G.nextOut(v1);
}
}
bool flag1; //保存图是否带权
void INIT(OLGragh<char>& G) //建图
{
cout<<"此图是否为带权图(是请输入1,不是请输入0):";
cin >> flag1;
int n=G.n();
char a,b;
cout <<"请输入初始状态时,图中各顶点的标号(以空格分隔)\n";
for(int i=0;i<n;i++)
{
cin >> a;
G.putVex(i,a);
}
cout <<"请输入初始状态时,图中边的数量:";
cin >> n;
cout <<"请输入初始状态时,图中边连接的顶点的标号\n"
<<"每行输入两个字母,以空格分隔\n"
<<"弧尾在前,弧头在后(带权图后加空格和权值)\n"
<<"例如:A B (带权:A B 3)为A指向B的边\n";
for(int i=0;i<n;i++)
{
int c=1;
cin >> a >> b;
int x=G.locateVex(a);
int y=G.locateVex(b);
if(flag1)
cin >>c;
G.setEdge(x,y,c);
}
}
void menu(OLGragh<char>& G) //菜单
{
int x,y,c;
char a,b;
int flag = 1;
while(flag)
{
cout <<"----------------------------------\n";
int t;
cout<<"0.退出程序\n"
<<"1.插入边\n"
<<"2.删除边\n"
<<"3.DFS输出顶点和出、入边的权之和(无权图则为出、入度)\n"
<<"请输入所需操作的序号:";
cin >> t;
switch(t)
{
case 0:
flag=0;
break;
case 1:
cout <<"请输入插入边的端点标号(和权)格式参照建图时边的输入的格式:";
c=1;
cin >> a >> b;
x=G.locateVex(a);
y=G.locateVex(b);
if(flag1)
cin >>c;
G.setEdge(x,y,c);
break;
case 2:
cout <<"请输入删除边的端点标号:";
cin >> a >> b;
x=G.locateVex(a);
y=G.locateVex(b);
G.delEdge(x,y);
break;
case 3:
cout <<"dfs输出结果为:\n";
for(int i=0;i<G.n();i++) //初始化标记数组
G.setMark(i,0);
for(int i=0;i<G.n();i++) //对非连通图的遍历
{
if(!G.getMark(i))
DFS(i,G);
}
break;
default:
cout <<"请输入正确的指令!!";
break;
}
cout <<"----------------------------------\n\n";
}
}
int main()
{
int n;
cout <<"本程序只支持有向图的储存,图的标号类型为字符\n";
cout <<"请输入本次建立图的顶点数量:";
cin >> n;
OLGragh<char> G(n);
INIT(G);
menu(G);
return 0;
}
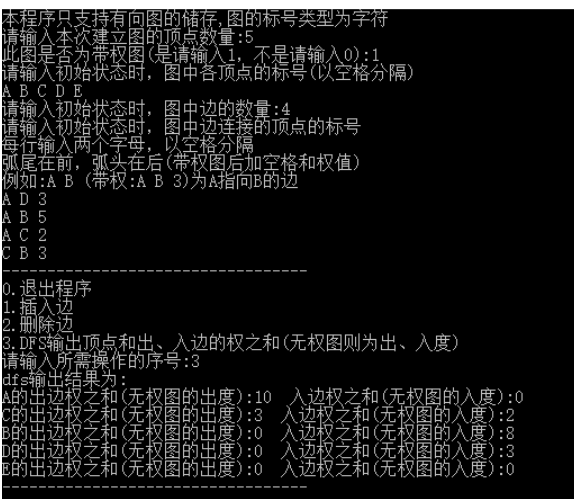
7.测试结果示例


 浙公网安备 33010602011771号
浙公网安备 33010602011771号