一、神经网络基础
-
人工神经元（Artificial Neuron）：又单神经元结构，叫受生物神经元（Biological Neuron）启发而构建的可微分计算单元，其设计融合了线性判别与非线性响应（门控）两个关键机制。是神经网络中前向传播的基本单位
神经元结构：对于输入样本\(\mathbf x=(x_1,x_2,\dots,x_n)^\top\in\mathbb R^n\)，权重 \(\pmb w=(w_1,w_2,\dots,w_n)^\top\in\mathbb R^n\) ，神经元执行两个计算逻辑
- 仿射变换（Affine Transformation）：对样本 ，进行线性加权 \(\mathbf{net}=\pmb w^\top\pmb x+b=\sum_{i=1}^nw_ix_i+b\) 作为净输入（Net Input），映射值通常命名为
net - 非线性激活（Nonlinear Activation）：将净输入经过激活函数 \(\mathbf{out} = f(\mathbf{net})\) 映射为净输出（Net Output），映射值通常命名为
out
- 仿射变换（Affine Transformation）：对样本 ，进行线性加权 \(\mathbf{net}=\pmb w^\top\pmb x+b=\sum_{i=1}^nw_ix_i+b\) 作为净输入（Net Input），映射值通常命名为
1.2 全连接前馈神经网络（Fully Connected Feedforward Network）：全连接神经网络（FCN），又称多层感知机（Multilayer Perceptron, MLP），是由多个单神经元按层堆叠而成的有向无环图（DAG），信息单向从前向后传播。通过多层非线性变换学习数据的层次化表示
- 层次化：层次化抽象是深度学习优于浅层模型的核心机制，网络深度决定了特征组合的阶数
- 能力：
- 自动提取特征：无需人工设计特征，网络通过端到端训练自动学习最优特征表示。
- 弱解释性（黑匣）：内部表示高度分布式且非符号化，难以解释决策逻辑（与符号 AI 形成对比）
- 数据依赖性强：性能高度依赖大规模标注数据，小样本场景易过拟合。
- 通用近似能力：单隐藏层 MLP 可以任意精度逼近紧集上的任何连续函数。
1、感知器（Perceptron）
感知器是最早的神经网络模型之一，由 Frank Rosenblatt 于 1957 年提出，用于解决二分类问题
1.1 定义激活函数：
- 输入层：\(z(w,x)=w_0+\sum_{i=1}^nw_ix_i\)
- 输出层：阶跃函数激活
\[f(x)=\text{step}(\omega,x)=
\begin{cases}1&z(\omega,x)>0\\0&z(\omega,x)\leqslant0\end{cases}\\
\]
import numpy as np
x = np.linspace(-6, 6, 400)
fz = lambda z: np.asarray(z>0, dtype=int)
1.2 损失函数
构建损失函数：仅当感知器预测错误时对权重进行更新，即存在样本 \(x_i\) 的 预测值 \(\hat y_i\neq\) 真实值 \(y_i\) 时对梯度进行更新
-
方式一：
- 若真实值 \(y=1\) 时 预测结果 \(\hat y=-1\)，说明权重偏小，应当使权重增大，更新：\(w=w+\eta x\)；
- 同理，若真实值 \(y=0\) 时 预测结果 \(\hat y=1\)，说明权重偏大，应当使权重增小，更新：\(w=w-\eta x\)；
- \(\Rightarrow\) 权重更新规则：\(w=w+\eta(y-\hat y)x\)
-
方式二：采用随机梯度下降SGD更新权重
- 利用损失函数进行梯度更新：\(J(w)=\sum_{x_i\in M}\frac{|\vec w^\top\vec x^{(i)}|}{\|\vec w\|}=\sum_{x_i\in M}\frac{-y^{(i)}(\vec w^\top\vec x^{(i)})}{\|\vec w\|}\\\)
- 其中，\(M\)：所有分类样本的错误集
- 梯度下降：\(\frac{\partial J(w)}{\partial w_j}=\sum_{i=M}-y^{(i)}x_j^{(i)}\Rightarrow\\\) 梯度更新：\(w_j=w_j+\eta\sum_{i\in M}y^{(i)}x_j^{(i)}\\\)
- 实际仅当分类错误时进行梯度更新：\(w_j=w_j+\eta (y^{(i)}-\hat y^{(i)})x_j^{(i)}\\\)
- 利用损失函数进行梯度更新：\(J(w)=\sum_{x_i\in M}\frac{|\vec w^\top\vec x^{(i)}|}{\|\vec w\|}=\sum_{x_i\in M}\frac{-y^{(i)}(\vec w^\top\vec x^{(i)})}{\|\vec w\|}\\\)
1.3 手动代码实现：
import numpy as np
class Perception:
def __init__(self, learning_rate=0.1, epochs=10):
self.learning_rate=learning_rate
self.epochs=epochs
def fit(self, X, y):
X, y = np.asarray(X), np.asarray(y)
self.coef_ = np.random.random(X.shape[1])
self.intercept_ = np.random.random()
self.errors_ = []
for _ in range(self.epochs):
idx = np.random.permutation(X.shape[0])
error_ = 0
for xi, yi in zip(X[idx], y[idx]):
zi=self.z(xi)
yi_pred=self.step(zi)
error_ += yi_pred != yi
# 更新权重
self.coef_ += self.learning_rate * (yi - yi_pred) * xi
self.intercept_ += self.learning_rate * (yi - yi_pred)
self.errors_.append(error_)
if not error_:
break
def z(self, x):
return np.dot(x, self.coef_)+self.intercept_
def step(self, z):
return np.asarray(z>0, dtype=int)
def predict(self, X):
z = self.z(X)
return self.step(z)
局限性：对于线性可分数据集一定可以收敛，但线性不可分数据集（如XOR问题）无法对其进行拟合
2、自适应神经网络
2.1 介绍
- 由 Bernard Widrow 和 Ted Hoff 于 1960 年提出 Adaptive Linear Neuron 自适应线性单元（Adaline），是感知器的重要改进版本。它通过引入连续输出和可微损失函数，使得模型能够完成回归任务，但仍不具备非线性建模能力。
- 对感知器的改进：
- 使用线性激活函数，而感知器使用阶跃函数
- 损失函数：使用平方和损失函数SSE考虑了所有样本（感知器仅考虑分类错误的样本）
- 应用：能够实现二分类和回归任务（感知器仅能实现二分类）
- 收敛性：数据线性不可分时，Adaline仍可收敛（感知器无法收敛），
- 但Adaline仍无法解决线性不可分问题
2.2 损失函数
使用均方误差MSE评估损失函数 \(J(w)=\frac1{2m}\sum_{i=1}^m(y^{(i)}-\hat y^{(i)})^2\)，其中 \(\hat y^{(i)}=\text{activation}(z^{(i)})=z^{(i)}=\pmb w^\top\pmb x^{(i)}+w_0\)
梯度更新：\(\frac{\partial J(w)}{\partial w_j}=-\frac1m\sum_{i=1}^m(y^{(i)}-\hat y^{(i)})x_j^{(i)},\frac{\partial J(w)}{\partial w_0}=-\frac1m\sum_{i=1}^m(y^{(i)}-\hat y^{(i)})\\\)
- 使用随机梯度下降SGD，对单个样本更新：\(w_j\leftarrow w_j+\eta(y^{(i)}-\hat y^{(i)})x^{(i)}_j\)
- 使用批量梯度下降BGD，对所有样本更新：\(w\leftarrow w+\frac\eta m\pmb X^\top(\pmb y-\pmb{\hat y})\)
2.3 手动代码实现
import numpy as np
from typing import Literal
class AdaLine:
def __init__(
self,
learning_rate:float=0.1,
epochs:int=10,
task:Literal['regression','classification']='regression',
GDmethod:Literal['SGD','BGD','MBGD']='MBGD',
batch_size:int=1,
tol:float=1e-4):
'支持三种随机梯度下降，支持分类任务和回归任务，支持早停'
self.learning_rate=learning_rate
self.epochs=epochs
self.task=task
self.GDmethod=GDmethod
self.batch_size=batch_size
self.tol=tol
def activation(self, z):
"定义激活函数：AdaLine中使用线性激活函数f(z)=z"
return z
def z(self, X):
return np.dot(X, self.coef_) + self.intercept_
def compute_loss(self,X,y):
"计算MSE，考虑所有样本"
y_pred = self.predict(X)
return np.mean(np.square(y - y_pred))
def fit(self, X, y):
X, y = np.asarray(X), np.asarray(y)
self.coef_ = np.zeros(X.shape[1])
self.intercept_ = 0.0
self.loss_history_ = []
batch_dict={
'BGD':X.shape[0],
'SGD':1,
'MBGD':self.batch_size
}
for _ in range(self.epochs):
idx=np.random.permutation(X.shape[0])
X, y=X[idx], y[idx]
for start in range(0, X.shape[0], batch_dict[self.GDmethod]):
end=min(start+batch_dict[self.GDmethod], X.shape[0])
xi, yi = X[start:end], y[start:end]
yi_pred = self.predict(xi)
yi_diff = yi - yi_pred
# 更新权重
self.coef_ += np.dot(xi.T, yi_diff) * self.learning_rate / xi.shape[0]
self.intercept_ += self.learning_rate * yi_diff.mean()
self.loss_history_.append(self.compute_loss(X, y))
if self.compute_loss(X, y) < self.tol:
break
def predict(self, X):
z = self.z(X)
out = self.activation(z)
if self.task == 'regression':
return out
return np.where(z > 0, 1, 0)
3、激活函数（Activation Function）
3.1 激活函数的意义：
神经网络中引入非线性能力的关键组件。没有它，无论网络有多少层，都等价于一个线性模型。
- 线性模型的局限性
考虑一个无激活函数的多层神经网络：
\[\mathbf{y} = \mathbf{W}_2 (\mathbf{W}_1 \mathbf{x} + \mathbf{b}_1) + \mathbf{b}_2 = (\mathbf{W}_2 \mathbf{W}_1) \mathbf{x} + (\mathbf{W}_2 \mathbf{b}_1 + \mathbf{b}_2)
\]
这仍然是仿射变换（线性 + 偏置）！无论堆叠多少层，结果仍是 \(\mathbf{y} = \mathbf{W} \mathbf{x} + \mathbf{b}\)。
✅ 结论：若无非线性激活函数，深度神经网络 ≡ 单层线性模型。
- 激活函数的作用
- 引入非线性，使网络能拟合任意复杂函数（万能近似定理）
- 控制神经元输出范围（如 \([0,1]\) 或 \([-1,1]\)）
- 影响梯度传播（训练稳定性）
3.2 激活函数的历史演进
| 年代 | 激活函数 | 特点 | 局限 |
|---|---|---|---|
| 1943 | 阶跃函数（McCulloch & Pitts） | 模拟生物神经元“发放/不发放” | 不可导，无法用梯度下降 |
| 1980s | Sigmoid / Tanh | 光滑、可导、有界 | 梯度消失、输出非零中心 |
| 1990s | ReLU（首次提出） | 计算简单、缓解梯度消失 | “死神经元”问题 |
| 2010s | ReLU 变体（Leaky ReLU, ELU, PReLU） | 改善 ReLU 缺陷 | 超参敏感 |
| 2017–2020 | Swish / GELU | 自门控、平滑、性能优 | 计算稍复杂 |
| 2020s+ | SiLU / Mish / GELU（Transformer 常用） | 平衡性能与效率 | 成为现代架构默认选择 |
🔑 关键转折点：2012 年 AlexNet 使用 ReLU，大幅加速训练，引爆深度学习革命。
3.3 核心概念与数学定义
定义：激活函数是一个逐元素作用的非线性函数：
\[\mathbf{a} = f(\mathbf{z}), \quad \text{其中 } z_i = \mathbf{w}_i^\top \mathbf{x} + b_i
\]
即对每个神经元的加权输入 \(z\) 应用 \(f(z)\)。
理想激活函数应具备：
- 非线性：非仿射函数。ReLU 虽无界，但因其分段线性且非仿射，仍满足 UAT 条件
- 饱和区域小 → 避免梯度在训练初期就消失。
- 饱和区：梯度接近零 → 反向传播时梯度逐层衰减 → 梯度消失（Vanishing Gradient），导致浅层参数几乎不更新。
- 理想正向无饱和：\(z\rightarrow+\infty 时 f'(z)\nrightarrow0\) ，保证信息正向流动
- 理想负向弱饱和或无饱和：允许负输入有非零梯度（如 Leaky ReLU, ELU）
- Sigmoid/Tanh 时需特殊权重初始化（Xavier），而 ReLU 允许更简单的 He 初始化
- 近似0均值化（Approximately Zero-Centered Output）→ 加速收敛，减少“zig-zag”更新。
- 若激活输出均值 E[a]≫0（如 Sigmoid 输出 ∈ (0,1)），则下一层权重的梯度符号趋于一致，导致优化路径呈锯齿状震荡（zig-zagging），降低收敛效率。
- 数学解释：对于全连接层 \(y = \mathbf Wx + b\)，若 x 非零均值，则 \(\frac{\partial \mathcal L}{\partial\mathbf W_{ij}} = \frac{\partial \mathcal L}{\partial\mathbf y_i}x_j\) 的期望不为零，引入协方差偏移（Covariate Shift）
- 解决方案：
- 可导（至少几乎处处可导）→ 支持反向传播，支持基于梯度的优化算法（SGD, Adam 等）
- ReLU 在 z=0 处不可导，但该点测度为零（Lebesgue measure zero），实践中取次梯度（subgradient）\(\partial f(0)=[0,1]\)，通常设为 0 或 1。
- 现代框架（PyTorch/TensorFlow）对不可导点有默认处理策略，不影响训练。
- 例外：阶跃函数、Sign 函数等处处不可导，无法用标准反向传播，需借助 Straight-Through Estimator (STE) 等近似方法（用于二值神经网络）
- 计算高效（计算量小） → 低训练/推理延迟、低资源消耗
- 量化指标：
- FLOPs（浮点运算次数）
- 内存访问次数（Memory Access）
- 硬件友好性（是否支持 SIMD、GPU 加速）
- 量化指标：
- 避免梯度消失/爆炸 → 保证深层网络可训练性
- 理想正区梯度稳定：ReLU 在 \(z>0\) 时 \(f'(z)=1\)，梯度无衰减
- 理想负区梯度可控：Leaky ReLU (\(f'(z)=\alpha\))，ELU (\(f'(z)=\alpha e^z\)) 避免完全死亡。
- 解决方案：
- 残差连接（ResNet）：通过 skip connection 绕过激活函数，直接传递梯度
- 归一化技术（BN/LN）：稳定输入分布，间接控制激活值范围
- 输出有合理范围 → 加速收敛，促进信号在层间稳定传播
- 信号传播理论：
- 理想情况下，前向传播时激活值的方差应保持稳定（避免逐层放大或缩小）。
- 反向传播时梯度的方差也应稳定。
- He 初始化：对 ReLU，权重应按 \(\mathcal N(0,\sqrt{\frac2{n_m}})\) 初始化，使得 \(Var(a)≈Var(x)\)。
- 举例：
- GELU：输出分布接近高斯，利于优化。
- Swish/SiLU：平滑且非单调，在深层网络中表现出更稳定的梯度流
- 信号传播理论：
3.4 主流激活函数详解
- Linear恒等函数
\[\boxed{f(z)=z}
\]
- 用途：回归任务输出层
- 缺点：无非线性 → 多层网络退化为线性
- step阶跃函数
\[\boxed{f(z)=\begin{cases}1,&z>0\\0,&z\leq0\end{cases}}
\]
- 用途：McCulloch-Pitts 神经元模型；神经网络理论入门学习
- 缺陷：
- 处处不可导 → 无法使用梯度下降
- 仅处理完全线性可分的二分类问题
- Sigmoid（Logistic 函数）
\[\boxed{\sigma(z) = \frac{1}{1 + e^{-z}}}
\]
- 优势：
- 输出范围：\((0, 1)\)
- 导数：\(\sigma'(z) = \sigma(z)(1 - \sigma(z))\) → 光滑可导
- 概率解释（用于二分类输出层）
- 缺点：
- 梯度饱和：当 \(|z| > 4\) 时，\(\sigma'(z) \approx 0\) → 梯度消失
- 输出非零中心 → 导致梯度更新呈“锯齿状”，减慢收敛
- 梯度消失：❌不推荐用于隐藏层，不利于深度神经网络的训练
- Tanh（双曲正切）
\[\boxed{\tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}} = 2\sigma(2z) - 1}
\]
- 优势：
- 输出范围：\((-1, 1)\)
- 导数：\(\tanh'(z) = 1 - \tanh^2(z)\)
- 零中心（zero-centered）【适用于作为RNN的激活函数】，比 Sigmoid 更适合隐藏层
- 缺点：
- 仍存在梯度消失问题（当 \(|z|\) 大时导数趋近 0）
- ⚠️ 在 ReLU 出现前广泛使用，现已基本被取代。
- ReLU（Rectified Linear Unit）
\[\boxed{\operatorname{ReLU}(z) = \max(0, z) =
\begin{cases}z, & z > 0 \\0, & z \leq 0\end{cases}}
\]
- 优点：
- 导数：\(\operatorname{ReLU}'(z) =\begin{cases}1, & z > 0 \\0, & z < 0 \\\text{未定义}, & z = 0 \quad (\text{实践中取 } 0 \text{ 或 } 1)\end{cases}\)
- 计算极简（无指数对数运算）
- 梯度在正区恒为 1 → 缓解梯度消失
- 稀疏激活（约 50% 神经元输出为 0，提升效率）
- ✅ 2010s 最主流的隐藏层激活函数
- 缺点：
- 神经元死亡（Dead ReLU Problem）：若 \(z\) 长期 ≤ 0，梯度恒为 0，神经元“死亡”
- 输出非零中心
- Leaky ReLU（LReLU）
\[\boxed{\operatorname{LReLU}(z) =
\begin{cases}z, & z > 0 \\\alpha z, & z \leq 0\end{cases}
\quad (\alpha \text{ 通常取 } 0.01)}
\]
- 优点：
- 导数：\(\operatorname{LReLU}'(z) =\begin{cases}1, & z > 0 \\\alpha, & z < 0\end{cases}\)
- 负区保留小梯度 → 解决 Dead ReLU 问题
- 缺点
- 需手动设置超参数 \(\alpha\)
- Parametric ReLU (PReLU)
\[\operatorname{PReLU}(z) = \max(0, z) + \alpha \min(0, z)
\]
- 优点：
- 将 \(\alpha\) 变为**可学习参数 **，更灵活
- 在训练中通过反向传播优化 \(\alpha\)
- 在某些 CNN 架构（如 ResNet 变体）中表现优异
- 缺点：
- 增加参数量
- ELU（Exponential Linear Unit）
\[\boxed{\operatorname{ELU}(z) =
\begin{cases}z, & z > 0 \\
\alpha (e^z - 1), & z \leq 0\end{cases}}
\]
- 优点：
- 负区有非零梯度 → 减少 Dead Neuron
- 输出接近零均值 → 加速收敛
- 缺点：含指数运算 → 计算开销略高于 ReLU
-
Swish / SiLU（Google, 2017）
\[\boxed{\operatorname{Swish}(z) = z \cdot \sigma(\beta z)} \]- 用途： 现代 Transformer（如 BERT、ViT、LLaMA）常用激活函数
- 优点：
- 当 \(\beta = 1\) 时，称为 SiLU（Sigmoid Linear Unit）
- 导数：\(\frac{d}{dz} \operatorname{Swish}(z) = \sigma(\beta z) + \beta z \sigma(\beta z)(1 - \sigma(\beta z))\)
- 平滑、非单调（先减后增）
- 在深层网络中表现优于 ReLU
- 具备“自门控”机制（self-gating）
-
GELU（Gaussian Error Linear Unit）
\[\boxed{\operatorname{GELU}(z) = z \cdot \Phi(z) = z \cdot \frac{1}{2} \left[1 + \operatorname{erf}\left(\frac{z}{\sqrt{2}}\right)\right]} \]- 其中 ： \(\Phi(x)\) 是标准正态分布的累积分布函数（CDF）
- 近似实现（常用）：\(\operatorname{GELU}(x) \approx z \cdot \sigma(1.702z)\)
- 特点：
- 平滑、概率解释（“以概率 \(\Phi(x)\) 保留输入 \(x\)”）
- 在 NLP 和视觉大模型中表现优异（如 BERT、GPT、ViT）
-
Softmax
\[f(z_i)=\frac{e^{z_i}}{\sum_{j=1}^ne^{z_j}}=\frac{e^{z_i-\max(\mathbf z)}}{\sum_{j=1}^ne^{z_j-\max(\mathbf z)}}
\]
- 用途：多分类任务的输出层激活函数
- 优点：
- 输出为概率分布（和为 1，各项 \(\in (0,1)\)）
- 减去最大值防止溢出：避免上溢无法计算；下溢为零，仍可计算
-
Softplus
\[\boxed{\operatorname{softplut}(z)=\log(1+e^z)} \]- 用途：理论分析、需要可导性的场景
- 优点：
- ReLU 的光滑近似
- 导数：\(\sigma(z)\)（即 Sigmoid）
- 缺点：计算较 ReLU 复杂，实际使用较少
BN层，非饱和区收敛慢的问题
3.5 数学意义与理论支撑
万能近似定理（Universal Approximation Theorem）：一个具有单隐藏层和非线性激活函数的前馈神经网络，可以以任意精度逼近任何定义在紧集上的连续函数。
- 关键条件：激活函数必须是非线性的
- 意义：激活函数赋予神经网络“表达能力”
3.6 激活函数选择建议
| 场景 | 目的 | 推荐激活函数 |
|---|---|---|
| 隐藏层 | 通用，首选 | ReLU（简单有效）、SiLU / GELU（高性能） |
| 避免 Dead ReLU | Leaky ReLU / ELU | |
| Transformer / 大模型 | GELU / SiLU | |
| RNN / LSTM | Tanh（传统）、ReLU（需谨慎） | |
| 输出层 | 二分类 | Sigmoid |
| 多分类 | Softmax（注意：Softmax 不是激活函数，是归一化函数） | |
| 回归 | Linear（Identity） | |
| 需避免使用 | Sigmoid / Tanh 作为隐藏层（梯度消失风险高） |
收敛速度：\(\text{Sigmoid} < \text{Tanh} \ll \text{ReLU} \leq \text{Leaky ReLU} < \text{SiLU / GELU}\)
3.7 总结
| 激活函数 | 非线性 | 可导 | 梯度稳定 | 零中心 | 计算效率 |
|---|---|---|---|---|---|
| Sigmoid | ✅ | ✅ | ❌ | ❌ | 中 |
| Tanh | ✅ | ✅ | ❌ | ✅ | 中 |
| ReLU | ✅ | ⚠️（分段） | ✅（正区） | ❌ | 高 |
| Leaky ReLU | ✅ | ✅ | ✅ | 近似 | 高 |
| GELU/SiLU | ✅ | ✅ | ✅ | 近似 | 中 |
💡 核心思想：激活函数是神经网络的“开关”与“调节器”，它决定了信息如何被非线性地转换与传递。
- 在 ResNet、Transformer 中的具体应用
- 激活函数与 Batch Normalization 的协同作用
二、人工神经网络
1、多层感知器
概念：MLP，Multi-Layer Perceptron
又叫深度前馈网络（deep feedforward netword），前馈神经网络（feedforward neural netword）
2、🧠神经元网络
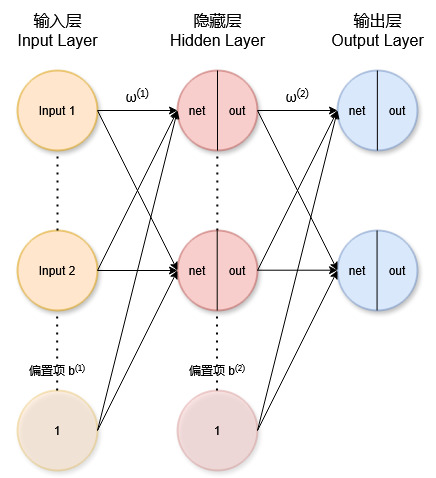
一个典型的全连接前馈神经网络包含三层：
| 层级 | 组成 | 说明 |
|---|---|---|
| 输入层（Input Layer） | (\(\mathbf x_1, \mathbf x_2, \dots\)) | 接收原始特征，无计算（不计入“层数”） |
| 隐藏层（Hidden Layer） | (\(\mathbf{net}_{h}, \mathbf{out}_{h}\)) | 对输入做线性组合 + 非线性激活 |
| 输出层（Output Layer） | (\(\mathbf{net}_{o}, \mathbf{out}_{o}\)) | 生成最终预测值 |
✅ 每个神经元 = 线性加权（net） + 激活函数（out）
2.1 🔁前向传播 Forward Propagation：
前向传播：信息通过神经元从输入 → 隐藏 → 输出逐层传递。
-
传播过程：\(\mathbf{out}^{(l-1)} \xrightarrow{\text{linear}} \mathbf{net}^{(l)} \xrightarrow{f(\cdot)} \mathbf{out}^{(l)}\)
net：净输入out：激活输出- 上一层神经元的
out经过线性加权为下一层神经元的net，net再经过神经元内部激活函数激活为out，如此循环完成前向传播。
-
所有中间变量（
net和out）均需被记录，用于后续反向传播。 -
回归任务无激活函数，但可视为输出层采用恒等函数（Linear, \(f(x)=x\)）作为激活函数。
-
以两层神经网络为例（1层隐藏层+1层输出层）。
-
下图正确描述了神经网络。每个圆代表一个神经元（偏置项和输入层不作为神经元），分为
net和out两部分；箭头上的 \(w^{(l)}\) 表示第 \(l\) 层的权重；偏置项 \(b\) 通过常数 \(1\) 连接。
前向传播过程：\(\mathbf{Input}^{(0)} \rightarrow \text{net}^{(1)} \rightarrow \text{out}^{(1)} \rightarrow \text{net}^{(2)} \rightarrow \text{out}^{(2)}\)![神经元网络1]()
-
输入层（无计算，不计入层数）
矩阵表示：- 输入样本矩阵： \(\mathbf X\in\mathbb R^{N\times d}\)（\(N\) 个样本，\(d\) 个特征）
-
隐藏层 hidden layer 计算
对第 \(j\) 个隐藏层神经元：
\[\boxed{\begin{align} &\mathbf{net}_j^{(1)} = \sum_{i=1}^{d} w_{ji}^{(1)}\mathbf x_i + b_j^{(1)}\\ &\mathbf{out}_j^{(1)} = f(\mathbf{net}_j^{(1)}) \end{align}} \]矩阵表示：
- \(\mathbf{Net}^{(1)}=\mathbf{XW}^{(1)\top}+\mathbf{b}^{(1)},\mathbf{Out}^{(1)}=f(\mathbf{Net}^{(1)})\)
-
输出层 output layer 计算
对第 \(j\) 个输出神经元 \(o_j\)\[\boxed{\begin{align} &\mathbf{net}_j^{(2)} = \sum_{i=1}^{n^{(1)}} w_{ji}^{(2)}\cdot\mathbf{out}_i^{(1)}+ b_j^{(2)}\\ &\mathbf{out}_j^{(2)} = f(\mathbf{net}_j^{(2)}) \end{align}} \]矩阵表示：
- \(\mathbf{Net}^{(2)}=\mathbf{Out}^{(1)}\mathbf W^{(2)\top}+\mathbf{b}^{(2)},\mathbf{Out}^{(2)}=f(\mathbf{Net}^{(2)})\)
-
总结发现符号规律及数据结构：
-
标量/向量
\[\boxed{\begin{align} &\mathbf{net}_j^{(l)} = \sum_{i=1}^{n^{(l-1)}} w_{ji}^{(l)}\cdot\mathbf{out}_i^{(l-1)}+ b_j^{(l)}\\ &\mathbf{out}_j^{(l)} = f(\mathbf{net}_j^{(l)})\\ \end{align}} \]- 其中：
- 激活输出：
- \(\mathbf{out}_i^{(l-1)}\in\mathbb R^N\) ，表示第 \(l-1\) 层第 \(i\) 个神经元的激活输出（特征值），\(i\in\{1,2,\dots,n^{(l-1)}\}\)。特别地，当 \(l=1\) 时，\(\mathbf{out}_i^{(0)}=x_i,n^{(0)} = d\) ；
- \(\mathbf{out}_j^{(l)}\in\mathbb R^N\) ，表示第 \(l\) 层第 \(j\) 个神经元的激活输出（特征值），\(j\in\{1,2,\dots,n^{(l)}\}\)。
- 净输入：\(\mathbf{net}_j^{(l)}\in\mathbb R^N\) ，表示第 \(l\) 层第 \(j\) 个神经元的净输入，\(j\in\{1,2,\dots,n^{(l)}\}\)。
- 权重：\(w_{ji}^{(l)}\in\mathbb R\) ，表示从第 \(l-1\) 层第 \(i\) 个神经元到第 \(l\) 层第 \(j\) 个神经元的连接权重
- 偏置项：\(b_j^{(l)}\in\mathbb R\) ，表示第 \(l\) 层第 \(j\) 个净输入的偏置项
- 激活输出：
- 其中：
-
矩阵
\[\boxed{\begin{align} &\mathbf{Net}^{(l)}=\mathbf{Out}^{(l-1)}\mathbf W^{(l)\top}+\mathbf{b}^{(l)}\\ &\mathbf{Out}^{(l)}=f^{(l)}(\mathbf{Net}^{(l)}) \end{align}} \]- 其中：
- 样本矩阵：\(\mathbf X\in\mathbb R^{N\times d}\)（\(N\) 个样本，\(d\) 个特征）
- 权重矩阵：\(\mathbf W^{(l)}\in\mathbb R^{n^{(l)}\times n^{(l-1)}}\) ($n^{(l)} $：第 \(l\) 层神经元数量，特别地 $n^{(0)} = d $)
- 偏置向量：\(\mathbf b^{(l)}\in\mathbb R^{n^{(l)}}\) （广播到 \(N\) 行）
- 净输入矩阵：\(\mathbf{Net}^{(l)}\in\mathbb R^{N\times n^{(l)}}\)
- 激活输出矩阵：\(\mathbf{Out}^{(l)}\in\mathbb R^{N\times n^{(l)}}\)
- \(l=1\)，即隐藏层（第一层）时，\(\mathbf{Out}^{(0)}=\mathbf{X}\)
- 其中：
-
-
📉损失函数：\(E_{\text{total}} = \sum_jE_{oj} + \frac\lambda2\sum_{l=1}^L\|\mathbf W^{(l)}\|_F^2\\\)，其中：
- \(\text{target}_{o_j}\)：真实值；\(\text{out}_{o_j}\)：预测值；
- 取 \(E=\sum_jE_{oj}\) ，\(j\in\{1,2,\dots,n_o\}\) ，此时 \(n_o\) 表示输出层神经元数，
- \(L\)：神经网络总层数；
- \(\lambda\)：正则强度
- \(\|\mathbf W^{(l)}\|_F^2=\sum_{j=1}^{n^{(l)}}(\mathbf w_j^{(l)})^2\)
- Frobenius 范数：\(\|\mathbf A\|_F=\sqrt{\sum_{i,j}A_{i,j}^2}=\sqrt{\text{tr}{(\mathbf A^\top\mathbf A)}}\)
回归任务使用均方误差（MSE）：\(E_{o_j} = \frac12( \text{target}_{o_j} - \text{out}_{o_j} )^2\)
分类任务使用交叉熵
2.2 🔙反向传播（Backpropagation）
反向传播：计算损失函数，逐层计算对各权重的梯度，最后再一并进行更新（不能边算边更新）
-
我们约定：
-
\(\mathbf{error}^{(l)}_j = \frac{\partial E}{\partial\mathbf{out}_j^{(l)}},\mathbf{Error}^{(l)}=\frac{\partial E}{\partial \mathbf{Out}^{(l)}}\in\mathbb R^{N\times n^{(l)}}\)
-
\(\mathbf{delta}^{(l)}_j = \boldsymbol \delta^{(l)}_j = \frac{\partial E}{\partial \mathbf{net}_j^{(l)}},\boldsymbol{\delta}^{(l)} = \frac{\partial E}{\partial \mathbf{Net}^{(l)}}\in\mathbb R^{N\times n^{(l)}}\) ，反向传播的核心中间量
目标：计算损失 \(E\) 对所有参数的梯度，再进行参数更新
-
-
计算输出层的权重梯度：
\[\boxed{\begin{align} &\mathbf{error}_j^{(2)} = \frac{\partial\mathbf E}{\partial \mathbf{out}_j^{(2)}}\\ &\pmb\delta_j^{(2)} = \frac{\partial\mathbf E}{\partial \mathbf{net}_j^{(2)}} = \mathbf{error}_j^{(2)} \cdot \frac{\partial \mathbf{out}_j^{(2)}}{\partial \mathbf{net}_j^{(2)}}\\ &\frac{\partial\mathbf E}{\partial \omega_{ji}^{(2)}} = \pmb\delta_j^{(2)} \cdot \frac{\partial \mathbf{net}_j^{(2)}}{\partial \omega_{ji}^{(2)}} \end{align}} \]其中：
- 可求 \(\mathbf{error}_j^{(2)} = -(\text{target}_{oj} - \text{out}_{oj})\)
- 可求 \(\frac{\partial \mathbf{out}_j^{(2)}}{\partial \mathbf{net}_j^{(2)}} =f'(\mathbf{net}_j^{(2)})\)
- \(\Rightarrow \boldsymbol\delta_j^{(2)} = -(\text{target}_{oj} - \text{out}_{oj})\cdot f'(\mathbf{net}_j^{(2)}) \Rightarrow\boldsymbol\delta^{(2)}=(\mathbf{Out}^{(2)}-\mathbf{Target}^{(2)})\odot f'(\mathbf{Net}^{(2)})\)
- 因为 \(\mathbf{net}_j^{(2)} = \sum_{i=1}^{n^{(l-1)}} w_{ji}^{(2)}\cdot\mathbf{out}_i^{(1)}+ b_j^{(2)}\) 可求\(\frac{\partial \mathbf{net}_j^{(2)}}{\partial w_{ji}^{(2)}} = \mathbf{out}_i^{(1)},\frac{\partial E}{\partial b_j^{(l)}} = \boldsymbol\delta_j^{(2)}\)
- \(\Rightarrow \frac{\partial E}{\partial w_{ji}^{(2)}} = \boldsymbol\delta_j^{(2)} \cdot \mathbf{out}_i^{(1)} \Rightarrow \frac{\partial E}{\partial \mathbf W^{(2)}} = \boldsymbol\delta^{(2)\top} \mathbf{Out}^{(1)},\frac{\partial E}{\partial \mathbf b^{(2)}} = \boldsymbol{\delta}^{(2)\top} \mathbf{1}_N\)
-
计算隐藏层的权重梯度：
\[\boxed{\begin{align} &\mathbf{error}_i^{(1)} = \frac{\partial E}{\partial \mathbf{out}_i^{(1)}} = \sum_{j=1}^{n^{(1)}}\frac{\partial E}{\partial \mathbf{net}_j^{(2)}} \cdot \frac{\partial \mathbf{net}_j^{(2)}}{\partial \mathbf{out}_i^{(1)}}\\ &\pmb\delta_i^{(1)} = \frac{\partial E}{\partial \mathbf{net}_i^{(1)}} = \mathbf{error}_i^{(1)} \cdot \frac{\partial \mathbf{out}_i^{(1)}}{\partial \mathbf{net}_i^{(1)}}\\ &\frac{\partial E}{\partial \omega_{ji}^{(1)}} = \pmb\delta_i^{(1)} \cdot \frac{\partial \mathbf{net}_i^{(1)}}{\partial \omega_{ji}^{(1)}} \end{align}} \]其中：
- 可求 $\frac{\partial E}{\partial \mathbf {net}_j^{(2)}} = \boldsymbol\delta_j^{(2)} $
- 可求 \(\frac{\partial \mathbf {net}_{j}^{(2)}}{\partial \mathbf {out}_i^{(1)}} = w_{ji}^{(2)}\)
- \(\Rightarrow \mathbf{error}_i^{(1)} = \sum_{j=1}^{n^{(2)}}w_{ji}^{(2)}\boldsymbol\delta_j^{(2)} \Rightarrow \mathbf{Error}^{(1)} = \pmb\delta^{(2)}\mathbf W^{(2)}\in\mathbb{R}^{N \times n^{(1)}}\)
- 可求\(\frac {\partial \mathbf {out}_j^{(1)} } {\partial \mathbf {net}_{hj}} = f'(\mathbf {net}_i^{(1)})\)
- \(\Rightarrow \boldsymbol\delta_i^{(1)} = \mathbf{error}_i^{(1)} \cdot f'(\mathbf{net}_i^{(1)}) \Rightarrow \boldsymbol\delta^{(1)} = \mathbf{Error}^{(1)}\odot f'(\mathbf{Net}^{(1)})\)
- 因为 \(\mathbf{net}_j^{(1)} = \sum_{i=1}^d w_{ji}^{(1)}\mathbf x_i + b_j^{(l)}\) 可求 \(\frac{\partial \mathbf{net}_i^{(1)}}{\partial w_{ji}^{(1)}} = \mathbf x_i,\frac{\partial \mathbf{net}_i^{(1)}}{\partial b_i^{(1)}} = \boldsymbol\delta_i^{(1)}\)
- \(\Rightarrow \frac{\partial E}{\partial w_{ji}^{(1)}} = \boldsymbol\delta_j^{(1)} \cdot \mathbf x_i \Rightarrow \frac{\partial E}{\partial \mathbf W^{(1)}} = \boldsymbol\delta^{(1)\top} \mathbf X,\frac{\partial E}{\partial \mathbf b^{(1)}} = \boldsymbol\delta^{(1)}\mathbf{1}_N\in\mathbb R^{n^{(l)}}\)
-
总结发现符号规律及数据结构：
-
矩阵：
- 输出层（\(l=L\)）：\(\boxed{\mathbf{Error}^{(L)}=\frac{\partial E}{\partial \mathbf{Out}^{(L)}}\in\mathbb R^{N \times n^{(L)}}}\)
- 隐藏层（\(l<L\)）：\(\boxed{\mathbf{Error}^{(l)} = \pmb\delta^{(l+1)}\mathbf W^{(l+1)}\in\mathbb{R}^{N \times n^{(l)}}}\)
- \(\boxed{\boldsymbol\delta^{(l)}=\mathbf{Error}^{(l)} \odot f'^{(l)}(\mathbf{Net}^{(l)})\in\mathbb R^{N\times n^{(l)}}}\)
-
参数梯度：
\[\boxed{\begin{align} &\frac{\partial\text E_{total}}{\partial \mathbf W^{(l)}} = \boldsymbol \delta^{(l)\top}\mathbf{Out}^{(l-1)}+\lambda\mathbf W^{(l)}\in\mathbb R^{n^{(l)} \times n^{(l-1)}}\\ &\frac{\partial\text E_{total}}{\partial \mathbf b^{(l)}} = \boldsymbol \delta^{(l)\top}\mathbf 1_N\in\mathbb R^{n^{(l)}}\\ \end{align}} \]
-
2.3 🔄 优化算法
神经网络实际上是一个非凸、高维、可能病态（ill-conditioned）的优化问题：
\[\min_\theta\mathcal L(\theta)=\frac1m\sum_{i=1}^m\ell(y^{(i)}-\hat y^{(i)})+\lambda\Omega(\theta)
\]
-
其中：
- \(\theta=\{\mathbf W,\mathbf b\}\) 为所有可学习参数
- \(\ell\) 为损失函数
- \(\Omega\) 为正则项
-
梯度下降（Gradient Descent，GD）：\(\theta \leftarrow \theta - \eta \cdot \nabla_\theta\mathcal L(\theta)\)
-
其中：
- \(\nabla_\theta\mathcal L\Leftrightarrow\frac{\partial \mathcal L}{\partial \theta}\) ，两者表达仅形式不同，完全等价
- \(\eta\) ：学习率（Learning Rate），又称为学习步长
-
学习率调度策略（Learning Rate Scheduling）
- Step Decay：\(\eta_t = \eta_0 \cdot \gamma^{\frac tT}\) ，每 \(T\) 步衰减 \(\gamma\) 倍（如 \(\gamma = 0.1\) ）
- Exponential Decay：\(\eta_t = \eta_0 \cdot e^{-kt}\) ，平滑指数衰减
- Reduce on Plateau：\(\eta_t = \eta_{min} + \frac12(\eta_{max}-\eta_{min})(1+\cos(\frac{\pi t}T))\) ，余弦退火，常用于 warm restart
- Step Decay：\(\eta_t = \eta_0 \cdot \gamma^{\frac tT}\) ，每 \(T\) 步衰减 \(\gamma\) 倍（如 \(\gamma = 0.1\) ）
- 自适应，根据每次更新的梯度更新调整学习率，是学习率实现从大到小，从粗到精的过程
-
-
动量法
-
$ \eta $：学习率（learning rate）
-
梯度更新：动量法，采用指数加权平均，使每一次的更新受到历史经验的影响，距离本次更新越远的历史数据所占的权重越小。
浙公网安备 33010602011771号