4.06号开始的题解-4.20 不含4.19的cf
https://codeforces.com/contest/2084/problem/C

排除下不合理的情况 这些都是很容易想到的 就是交换麻烦了点
这里上芋老师的代码 有很多地方需要我学习下 写的就很精简
首先是这两个的不同
vector<array<int, 2>> a(n);

for (int j = 0; j < 2; j++) {
for (int i = 0; i < n; i++) {
cin >> a[i][j];
a[i][j]--;
}
}
vector<vector

然后介绍下他是如何交换的 写的很好
我们记录第一行的数字为要交换的下标 然后直接开始换就行 不需要去提前把位置规划好
碰到对称不等的
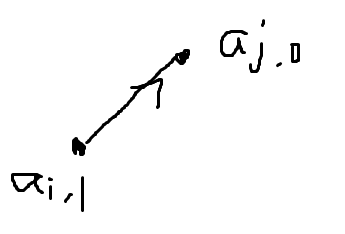
直接开换 我先找到我那个本来对称的下表 就是w[a[i][1]] 然后n-1-i和这个互换就行
然后维护好两排交换 首先是两排元素换下 然后再改下双方的w下表 颠倒下都行没影响的
auto swp = [&](int x, int y) -> void {
res.push_back({x, y});
swap(a[x], a[y]);
swap(w[a[x][0]], w[a[y][0]]);可以颠倒 没影响的
//swap(w[a[x][0]], w[a[y][0]]);
// swap(a[x], a[y]);
};
for (int i = 0; i < n / 2; i++) {
int j = n - 1 - i;
if (a[i][0] == a[i][1]) swp(i, n / 2);
if (a[i][1] != a[j][0]) swp(j, w[a[i][1]]);
}
https://codeforces.com/contest/2084/problem/D

从数组中,重复地删除给定长度子数组,求剩余元素的问题
是一个结论题

此题他需要分成两种情况 那就是能不能直接变成小于k 或者大于等于k的情况
小于k那么直接套结论 最终就只能剩下
下标为0-n%k-1 任何一段k的都会被删除完的
大于等于k的话 那很显然我们只有分成m+1 每一组尽量大点就行 显然最多来到n/m+1那么大 余数也是要放的 就第一个结论那想不到
第二个猜都猜到了
if (n - m * k < k) {
int w = n % k - 1;
vector<int>v;
for(int i=0;i<=w;i++)v.push_back(i);
int siz = v.size();
for (int i = 0; i <= n-1; i++) {
if(i%k<=w){
a[i]=i%k;
}
else a[i]=1e9;
}
for(int i=0;i<=n-1;i++)
cout<<a[i]<<" ";
cout << endl;
} else {
int temp = m + 1;
int cnt = n / temp;
int cntrem = n % temp;
//cntrem是肯定不能要的
for (int i = 1; i <= m + 1; i++) {
for (int j = 0; j <= cnt - 1; j++) {
cout << j << " ";
}
if (cntrem) {
cout << cnt << " ";
cntrem--;
}
}
cout << endl;
}
https://codeforces.com/contest/1789/problem/C

直接枚举每一个数出现的长度之和 对于未出现的的数组之中cnt*(m+1−cnt) 对于两两的也有一个贡献 C(n,2)
for(int i=1;i<=m;i++){
cin>>x>>y;
if(a[x]!=y){
cnt[a[x]]+=i-lst[a[x]],lst[a[x]]=-1;
lst[y]=i,a[x]=y;
}
}
for(int i=1;i<=n+m;i++) if(lst[i]!=-1) cnt[i]+=m-lst[i]+1;
int ans=0;
for(int i=1;i<=n+m;i++){
ans+=cnt[i]*(m+1-cnt[i]);
ans+=cnt[i]*(cnt[i]-1)/2;
}
https://codeforces.com/contest/2093/problem/E

非常板子的一题 我就不放代码了 我只想介绍下t的原因
std::function<bool(int mid)>check=[&](int mid)->bool{
if(mid==0)return 1;//跑不了这种情况 特判样例
set<int>s;
for(int i=0;i<=mid-1;i++)s.insert(i);
set<int>temp;//s要凑满 修改成 vector<bool>ww(mid,false);
// int num=a[1];
int num=0;
int cost=mid;
int w=mid; //int now=mid;
for(int i=1;i<=n;i++)
{
if(a[i]<mid&&temp.count(a[i])==0) //if(a[i]<mid&&!ww[a[i]])
{
temp.insert(a[i]); //ww[a[i]]=1; now--;
}
if(temp.size()==s.size())
{
num++;
if(num>=k)return 1;
temp.clear(); // ww.assign(mid, false);now=mid;
}
}
return 0;
};
https://codeforces.com/contest/1793/problem/C


可以直接写双指针 双指针以后里面最好写if 不要再写while 容易死循环 我没写出双指针 我四个栈做的 懒得放了
int l = 1, r = n, maxn = n, minn = 1;
while (l < r) {
if (l > r) {
cout << -1 << endl;return ;
}
if (a[l] == maxn) {
l++, maxn--;
continue;
}
if (a[l] == minn) {
l++, minn++;
continue;
}
if (a[r] == maxn) {
r--, maxn--;
continue;
}
if (a[r] == minn) {
r--, minn++;
continue;
}
cout<<l<<" "<<r<<endl;
return ;
}
https://codeforces.com/contest/1902/problem/D

这个题很难 首先我们存下xy前缀和的 存一个坐标的记录
然后判断她能不能经过 有三种可能性
我们在1-l-1 l r r+1 n 就过了
l r的判断最难 不过我们可以想清楚怎么判断呢 假设我们走到l-1
此时是x y 那么得到l r这一段的偏移量delta 如果说我们经过了这一个点的 假设st fin
至少我们有st-x fin-y的偏移量对吧 那么也就说
我们那个delta-(st-xl-1)+xl-1 肯定是存在的
化简得到xl-1+ xr -st yl-1+yr-fin存在
//#include<bits/stdc++.h>
//using namespace std;
//#define int long long
//#define debug cout<<endl<<"---------"<<endl;
int prex[range];
int prey[range];
void solve(int t) {
int n;
int q;
string s;
cin >> n >> q >> s;
s = ' ' + s;
map<int, vector<int>>ma;
ma[encode(0,0)].push_back(0);
for (int i = 1; i <= n; i++) {
if (s[i] == 'U') {
prey[i] = prey[i - 1] + 1;
prex[i] = prex[i - 1];
}
if (s[i] == 'D') {
prey[i] = prey[i - 1] - 1;
prex[i] = prex[i - 1];
}
if (s[i] == 'R') {
prey[i] = prey[i - 1];
prex[i] = prex[i - 1] + 1;
}
if (s[i] == 'L') {
prey[i] = prey[i - 1];
prex[i] = prex[i - 1] - 1;
}
ma[encode(prex[i], prey[i])] .push_back(i);
}
std::function<bool(int x, int l,int r)>check = [&](int x, int l,int r)->bool{
if(ma[x].size()==0)return 0;
vector<int>&temp=ma[x];
auto it=lower_bound(temp.begin(),temp.end(),l);//-begin可以得到下标
if(it==temp.end())return 0;
if(*it<=r){
return 1;
}//
return 0;
};
while (q--) {
int x, y, l, r;
cin >> x >> y >> l >> r;
int w = encode(x, y);
if (check(w, 0, l-1)) {
cout << "YES" << endl;
continue;
}
if (check(w, r, n)) {
cout << "YES" << endl;
continue;
}
int nx = prex[l - 1] + prex[r] - x;
int ny = prey[l - 1] + prey[r] - y;
w = encode(nx, ny);
if (check(w, l, r)) {
cout << "YES" << endl;
continue;
}
cout << "NO" << endl;
}
//#include<bits/stdc++.h>
//using namespace std;
//#define int long long
//#define debug cout<<endl<<"---------"<<endl;
int prex[range];
int prey[range];
void solve(int t) {
int n;
int q;
string s;
cin >> n >> q >> s;
s = ' ' + s;
map<int, vector<int>>ma;
ma[encode(0,0)].push_back(0);
for (int i = 1; i <= n; i++) {
if (s[i] == 'U') {
prey[i] = prey[i - 1] + 1;
prex[i] = prex[i - 1];
}
if (s[i] == 'D') {
prey[i] = prey[i - 1] - 1;
prex[i] = prex[i - 1];
}
if (s[i] == 'R') {
prey[i] = prey[i - 1];
prex[i] = prex[i - 1] + 1;
}
if (s[i] == 'L') {
prey[i] = prey[i - 1];
prex[i] = prex[i - 1] - 1;
}
ma[encode(prex[i], prey[i])] .push_back(i);
}
std::function<bool(int x, int l,int r)>check = [&](int x, int l,int r)->bool{
if(ma[x].size()==0)return 0;
vector<int>&temp=ma[x];
auto it=lower_bound(temp.begin(),temp.end(),l);//-begin可以得到下标
if(it==temp.end())return 0;
if(*it<=r){
return 1;
}//
return 0;
};
while (q--) {
int x, y, l, r;
cin >> x >> y >> l >> r;
int w = encode(x, y);
if (check(w, 0, l-1)) {
cout << "YES" << endl;
continue;
}
if (check(w, r, n)) {
cout << "YES" << endl;
continue;
}
int nx = prex[l - 1] + prex[r] - x;
int ny = prey[l - 1] + prey[r] - y;
w = encode(nx, ny);
if (check(w, l, r)) {
cout << "YES" << endl;
continue;
}
cout << "NO" << endl;
}
https://codeforces.com/contest/2094/problem/F

赛时用的偏移写法没过 其实只要分析m%k的关系就行了
void go() {
int n, m, k;
cin >> n >> m >> k;
vector a(n, vector<int>(m, 0));
if (m % k) {
int cur = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
a[i][j] = (cur++) % k + 1;
}
}
} else {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (i % 2 == 0) {
a[i][j] = j % k + 1;
} else {
a[i][j] = (j + 1) % k + 1;
}
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cout << a[i][j] << " ";
}
cout << endl;
}
}
https://codeforces.com/contest/1901/problem/C

说一个思路吧 其实每次都弄maxn+1就好了 关注一个相对大小 每次/2 数组最大最小的人不会变的
while(mini!=maxn){
mini=(mini+maxn+1)/2;
ans++;
temp.push_back(maxn+1);
}
//赛时只想到了+r 却不知道r+1
if(ans>n){
cout<<ans<<endl;return ;
}
cout<<ans<<endl;
for(auto i:temp){
cout<<i<<" ";
}
cout<<endl;
https://codeforces.com/contest/1901/problem/D

注意审题 要求你选一个i 而不是随机的 所以你要求一个最坏情况下的i
然后我们要想到一个i左边与右边 拆点去思考 最差的情况就是一个点从头开始和从尾巴开始
我们需要记录一个suf pre存最大的值 注意pre suf 他们的保存 肯定与你想的不同 pre是相对后
for(int i=n;i>=1;i--){
suf[i]=max(suf[i+1],a[i]+i-1);
}
for(int i=1;i<=n;i++){
pre[i]=max(pre[i-1],a[i]+n-i);
}
int ans=1e10;
for(int i=1;i<=n;i++)
{
int temp=a[i];
temp=max(temp,max(suf[i+1],pre[i-1]));
ans=min(ans,temp);
}
cout<<ans<<endl;
https://codeforces.com/contest/1895/problem/C

多模拟就会发现 对于一个数比如他长度为5可以拆1 4 前配3 也可以3 1 +2的
然后我们记录一个长度和sum和 去找 可以配对的
cnt1-now+cnt1:
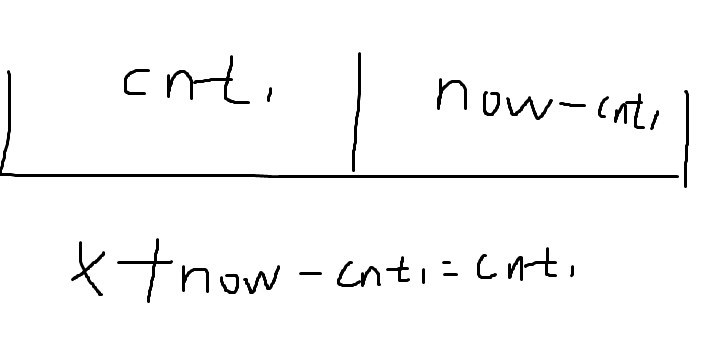
for(int i=1;i<=n;i++){
cin>>a[i];
int siz=a[i].size();
int now=0;
for(int j=0;j<siz;j++)
{
now+=a[i][j]-'0';
}
ma[{siz,now}]++;
}
int ans=0;
for(int i=1;i<=n;i++)
{
int siz=a[i].size();
int now=0;
for(int j=0;j<siz;j++)
{
now+=a[i][j]-'0';
}
int w=0;
int cnt1=0; int cnt2=0;
for(int j=1;j<=siz;j++){
w++;//w 表示前半段
cnt1+=a[i][j-1]-'0';
cnt2+=a[i][siz-1-j+1]-'0';
int rem=siz-w;
ans+=ma[{w-rem,cnt1-now+cnt1}];
if(j!=siz){
ans+=ma[{w-rem,cnt2-now+cnt2}];
}
}
}
cout<<ans<<endl;
https://codeforces.com/contest/1895/problem/D

attention题
b1^b2=a1
b2^b3=a2
...b1bi=a1--ai-1
很像高中数学题啊 说实话打算竞不就是高中做题吗
所以本质上此题就是维护一个异或和 01tire一下就行 此题选一个b1才是关键
01的话数组31就行 字符的话是最大字符长度n
#include<bits/stdc++.h>
#define int long long
#define debug cout<<endl<<"----------"<<endl;
const int range = 8e5+10;
using namespace std;
int n, k;
int a[range];
int ch[range][2];//
int idx;
int cnt[range];
void insert(int x) {
int p = 0;
int res = 0;
for (int i = 30; i >= 0; i--) {
int u = (x >> i) & 1;
if (!ch[p][u]) {
ch[p][u] = ++idx;
}
p = ch[p][u];
cnt[p] += 1;
}
return ;
}
int query(int x) {
int p = 0;
int res = 0;
for (int i = 30; i >= 0; i--) {
int u = bool((x >> i) & 1);
if (cnt[ch[p][!u]]) {
res += 1 << i;
p = ch[p][!u];
} else p = ch[p][u];
}
return res;
}
int pre[range];
void solve(int t ) { //多测
cin >> n ;
for(int i=1;i<=n-1;i++){
cin>>a[i];
pre[i]=pre[i-1]^a[i];
insert(pre[i]);
}
int ans=0;
for(int i=0;i<=n-1;i++)
{
if((query(i))<=n-1){
ans=i;//我了个不打括号就完蛋了
// debug
// cout<<i<<endl;
int w=query(i)^i;
// cout<<query(i)<<" "<<w<<endl;
break;;
}
}
cout<<ans<<" ";
for(int i=1;i<=n-1;i++)
{
cout<<(ans^pre[i])<<" ";
}
cout<<endl;
}
https://codeforces.com/contest/1879/problem/C

这题不难 无脑去找就行 注意审题 最终答案应该是

我没思考到阶乘 (样例都没过一遍就码了)
https://codeforces.com/contest/1886/problem/B
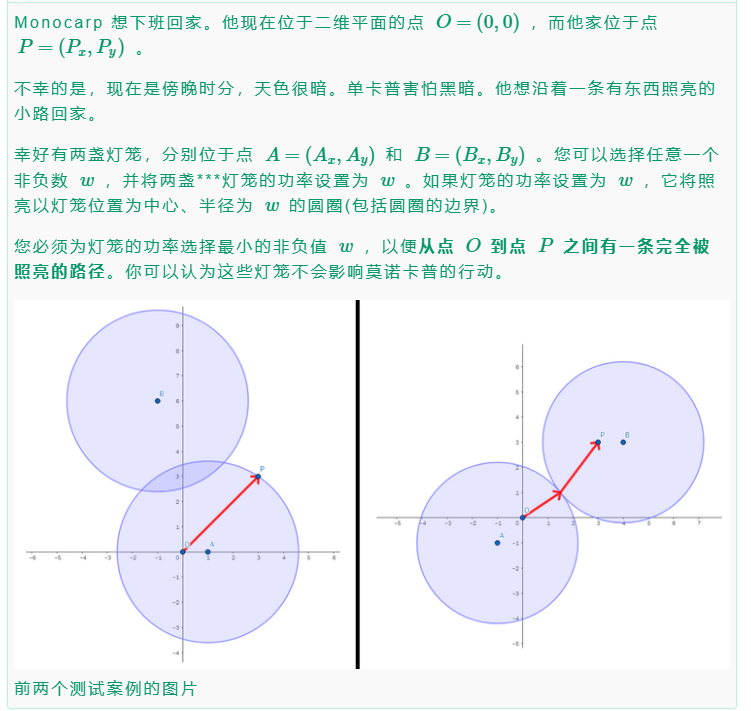
蛮难的 就是需要分类思考下
第一种就是离得很近 另一个点就没用了 相当于 ap----b这种 pa或者oa就行
另一种就是被夹中间了 就是图二 可能是ab/2相当于相切 当然不要忘记算oa ob
double cal(int x,int y,int xx,int yy ){
return sqrt((x-xx)*(x-xx)+(y-yy)*(y-yy))*1.0;
}
void init(){
}
void solve(int t)
{
int px,py;
int ax,ay;
int bx,by;
cin>>px>>py>>ax>>ay>>bx>>by;
//first
double ans=1e9;
ans=min(max(cal(0,0,ax,ay),cal(ax,ay,px,py)),ans);
ans=min(max(cal(0,0,bx,by),cal(bx,by,px,py)),ans);
double x=cal(0,0,ax,ay); double xx=cal(bx,by,px,py);
double xxx=cal(ax,ay,bx,by);
ans=min(ans,max(cal(0,0,ax,ay),max(cal(bx,by,px,py),cal(ax,ay,bx,by)*1.0/2.0)));
ans=min(ans,max(cal(0,0,bx,by),max(cal(ax,ay,px,py),cal(ax,ay,bx,by)*1.0/2.0)));
cout<<setprecision(9)<<fixed<<ans<<endl;
}
https://codeforces.com/contest/1861/problem/C

很有意思的一道题
显然我们可以让最后一个造成降序排列 这是肯定的 我也观察到了 (但是wa了)
然后考虑操作
+肯定无脑加 -就有说法了 如果减的是造成降序排列 要标记此时无降 否则没啥
1的话就看降序否 0同理 有些地方坑 比如<=1的数组是可以1的 注意10后及时更新

void solve(int t)
{
//题解思路真不错
string s;
cin>>s;
int unfcnt=0;
int fcnt=0;
int cnt=0;
bool flag=0;
for(int i=0;i<=s.size()-1;i++)
{
if(s[i]=='+')cnt++;
else if(s[i]=='1')
{
if(unfcnt==0){
fcnt=cnt;continue;
}
else flag=1;
}
else if(s[i]=='0')
{
if(cnt<2||fcnt==cnt){
flag=1;break;
}
if(unfcnt==0)unfcnt=cnt;
}
else if(s[i]=='-')
{
cnt--;
if(unfcnt>cnt)unfcnt=0;
else if(fcnt>cnt)fcnt=cnt;
}
}
if(flag){
cout<<"NO"<<endl;return ;
}
else {
cout<<"YES"<<endl;return ;
}
https://codeforces.com/contest/1860/problem/C

读懂题目很重要 翻一下 注意是bob先走 alice只是先选一个数字 然后选择是任意的一个前面的下标
然后这个数字不能选不能走的 然后问你最终谁不能走 不能走 就他赢的
其实一个很显然的结论就是 必胜态和必败态的转化
这里不讨论题解的树状数组优化上升子序列的写法

我们可以时刻记录一个最小值 只要可以跳这个最小值的时候 都是必胜态 然后1010101这样分布的
for(int i=1;i<=n;i++)
{
int win=0;
if(a[i]<now){
win=1;
now=a[i];
continue;
}
else {
if(a[i]>mini){
win=1;
}
else {
win=0;
mini=a[i];
}
}
if(win==0){
ans++;
}
}
cout<<ans<<endl;
https://codeforces.com/contest/1849/problem/A

我是for循环的 没想出来o1操作是这样的
cout<<min(n-2,m+k-1)*2+3<<endl;
https://codeforces.com/contest/1849/problem/C

一眼考虑缩小区间 那么如何缩小呢
很明显 0011 1 4->2 3
排序只有是10这种才会被排序 我们可以记录l的右边第一个1 和r左边第一个0 那么这种区间段就是要被排序的
//扇了自己10个巴掌 这没做出来
cin>>n>>m;
cin>>s;
s=' '+s;
pre[1]=1;
for(int i=0;i<=n+10;i++){
pre[i]=suf[i]=0;
}
//1->0
for(int i=2;i<=n;i++)
{
if(s[i]=='0')pre[i]=i;
else if(s[i]=='1'){
pre[i]=pre[i-1];
}
}
suf[n]=n;
//0->1
for(int i=n-1;i>=1;i--){
if(s[i]=='0'){
suf[i]=suf[i+1];
}
else {
suf[i]=i;
}
}
int ans=0;
//
map<pair<int,int>,bool>ma;
for(int i=1;i<=m;i++)
{
int l,r;
cin>>l>>r;
l=suf[l];
r=pre[r];
// cout<<l<<" "<<r<<" "<<ans<<endl;
if(l>=r){
l=r=0;
}
if(ma[{l,r}])continue;
ma[{l,r}]=1;
ans++;
}
cout<<ans<<endl;
https://codeforces.com/contest/1845/problem/C

题目有点读不懂 注意看其实是l-r选一个而不是 s序列里选一个 同时lr是m长 而不是一长一短
所以我们可以直接分析这个字符串 每次贪心的挑最远的相同字母(对于l-r之间的那个值)这样就可以一直跳着跳着了
//11:
//把一个数由右边向左边数,将奇位上的数字与偶位上的数字分别加起来,
//再求它们的差,
//如果这个差是11的倍数(包括0),那么,原来这个数就一定能被11整除。
//5:
//个位上是0或5的数都是5的倍数
//9
//一个数是9的倍数,当且仅当它的各个数字之和是9的倍数
string l;
string r;
string s;
set<int>st[50];
void solve(int t ) { //多测
//本题考察阅读理解 做了这么多题算难读懂的了
cin >> s;
cin >> m;
cin >> l >> r;
for(int i=0;i<=10;i++)st[i].clear();
for (int i = 0; i <= s.size() - 1; i++) {
int w = s[i] - '0';
st[w].insert(i);
}
int now = -1;
for (int i = 0; i < m; i++) {
int ww=0;
// cout<<endl;
// cout<<i<<endl;
for (int j = l[i] - '0'; j <= r[i] - '0'; j++) {
auto temp = st[j].upper_bound(now);
// cout<<*temp<<" ";
if (temp == st[j].end()) {
cout << "YES" << endl;
return ;
}
ww= max(ww, *temp);
}
now=max(now,ww);
}
cout<<"NO"<<endl;
https://codeforces.com/contest/1841/problem/C

这题实际上不是贪心的话很难!如果是贪心的话 其实证明是很复杂的 我是不会做的
只能提供题解思路了 我们对于一个数字是否修改有两只操作 一个是大一个是小
考虑我们修改是怎么找的
这里直接说了 对同一个数字而言 只管他的一左一右 你想想我改了中间的数 要是我右边还有数 那改小了没意义还变小了改大了右边改大了 没意义呀 因为你大了可能还造成之前的变负 除非你变E 你增的更多
左边是改大 而且是最左边 这样就好多了

int cal()
{
int val=0;
int maxn=0;
for(int i=n-1;i>=0;i--)
{
if((s[i]-'A'+1)>=maxn){
maxn=s[i]-'A'+1;
val+=qpow(10,s[i]-'A');
// cout<<val<<" "<<maxn<<endl;
}
else {
val-=qpow(10,s[i]-'A');
// cout<<val<<" "<<i<<endl;
}
}
return val;
}
void solve(int t)
{
//憧憬成为算法高手的一天
//nmmd 这题是真难
cin>>s;
n=s.size();
for(int i=1;i<=5;i++){
last[i]=-1;
st[i]=-1;
}
//这个写法很好 建议纳入板子
for(int i=n-1;i>=0;i--)
{
if(last[s[i]-'A'+1]==-1){
last[s[i]-'A'+1]=i;
}
st[s[i]-'A'+1]=i;
}
//gaid gai x
int ans=0;
ans=cal();
for(int i=1;i<=5;i++)
{
int now=st[i];
if(now!=-1)
{
for(int j=i+1;j<=5;j++)
{
// cout<<j<<endl;
// int now=st[i];
char ch='A'+j-1;
s[now]=ch;
ans=max(ans,cal());
s[now]='A'+i-1;
}
}
now=last[i];
// cout<<now<<endl;
if(now!=-1)
{
for(int j=1;j<=i-1;j++)
{
// int now=st[i];
char ch='A'+j-1;
s[now]=ch;
ans=max(ans,cal());
s[now]='A'+i-1;
}
}
}
cout<<ans<<endl;
https://codeforces.com/contest/1954/problem/C

这题还是说下吧 虽然直接切了 不过我的是贪心 没证明的 虽然这个证明自己是知道的

https://codeforces.com/contest/1954/problem/D

dp 此题的trick 就是关于这种集合类型的 比如说
1 2 3 分 1 2 13 2 3 的这种算贡献的 可以排序
然后按照数量排序 那么子集的最后一个数绝对是数量最大的 那么 计算贡献可以围绕这个数来展开 称为绝对众数
这题题目其实是很绕的 来解释下题目意思吧
其实 就是说给你2^n个集合 比如 1 2 3 问你把集合内的颜色的都放进去要多少个袋子 每一个袋子只能装两个球 比如说 我现在
3
1 1 2
放1 3 要多少个袋子 答案是2 因为 1 3 然后再3单独放
此题又为什么是dp呢 因为他其实是一个01背包 因为可以放可以不放 才有2^n种集合嘛
然后我们知道贡献怎么算 比如说 你此时是j个球 你绝对众数如果大于他 那很明显需要ai个袋子 否则是多少呢 其实 ai+j/2 (上) 多出来的
然后我们定义fj是放j个球的方案 然后 每次计算就好了
const int mod = 998244353;
int f[range];
void solve(int t) {
cin >> n;
int m=0;
//真的是阅读理解题 读懂就已经很费事了
for (int i = 1; i <= n; i++) {
cin >> a[i];
m+=a[i];
}
sort(a+1,a+1+n);
int ans = 0;
f[0]=1;
for (int i = 1; i <= n; i++) {
for(int j=0;j<=m-a[i];j++)
{
ans=(ans+(j>a[i]?(j+a[i]+1)/2:a[i])*f[j]%mod)%mod;
}
for(int j=m;j>=a[i];j--)
{
f[j]=f[j]+f[j-a[i]]%mod;
}
}
cout<<ans<<endl;



 浙公网安备 33010602011771号
浙公网安备 33010602011771号