P2966 [USACO09DEC] Cow Toll Paths G

题目

题外话

首先这道题目，我并不会写，我是看题解的，这道题目给我的感觉是一道模板，并没有很新颖的点，就是这个排序的操作是此题的核心.（我笔记本键盘找不到句号，姑且用这个‘.’吧）.

---

题目思路

这道题目为什么要排序呢？这是一个所有题解都在讨论的问题 我给出我的见解，红色的字是"权"

---

还有这题目并不是说求到了最短路，然后找出最短路的点权最大，就是此题答案，那不然太简单了，要的是和的最小值，注意审题了

---

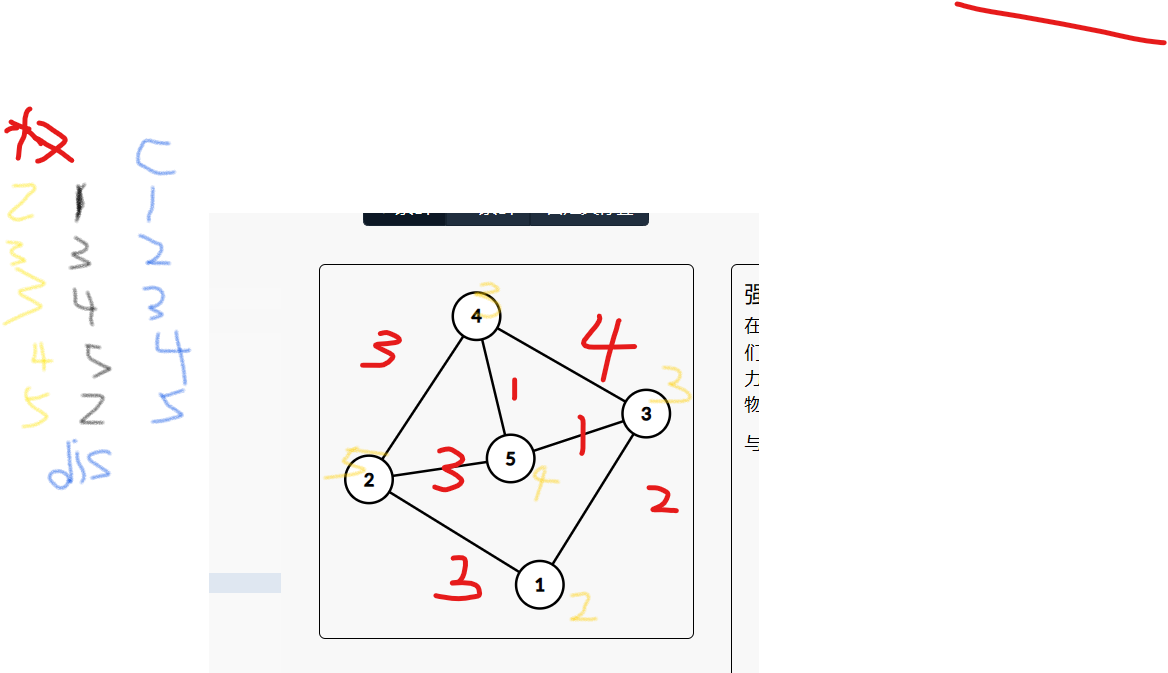
我们如果要求1-4的话 首先根据Floyd算法跑（不排序e数组）首先从1出发 会得到1-2 1-3 再是for循环中i来到2 出以1为转折点的2-5，2-4，2-1（不更新）， 而后是3，4，5

---

只有i，j的先后顺序进行遍历，比方说求1-5的最短路，1-3-5是最短的，

---

并且沿途点权最大值4加起来也是最小的相比1-2-5这些路径，但是我们求1--4的话 更新答案也是考1-3-5-4的，是2+1+1+max点权4=8，我们为什么敢直接肯定最大点权为5呢，

---

毕竟在更新的路劲中f[1[5]+max[1,5,4],没有考虑3，但实际我们走的就是1-3-5-4，按照题目给的路径中的最大点权来说1，3，4，5我们都是要比较的？

---

---

---

所以这就是排序的好处，避免了路径别的点的比较了，因为这个转折点我敢保证，一定比之前的转折点点权都大，所以不用去回顾之前的，

---

然后就是更新ans数组的方面了，在点权不断增大的情况下，如果f数组得不到更新，那ans数组也必然不会更新，因为点权不断增大了，

---

你都找不到一条比之前还短的路出来，加一个更大的数，结果必然比最优结果大呀

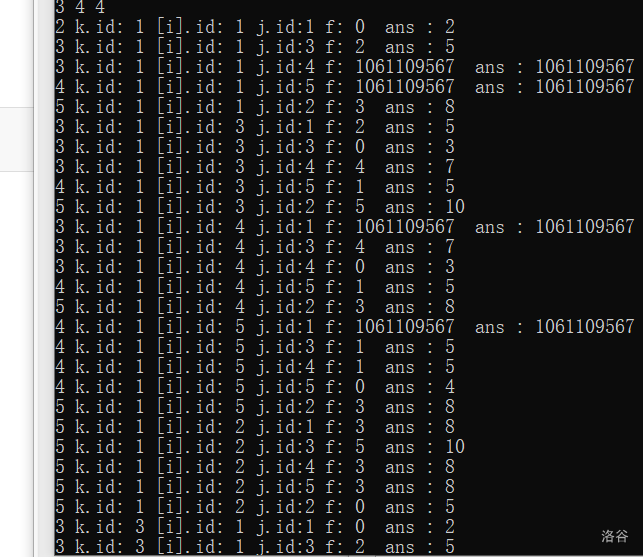
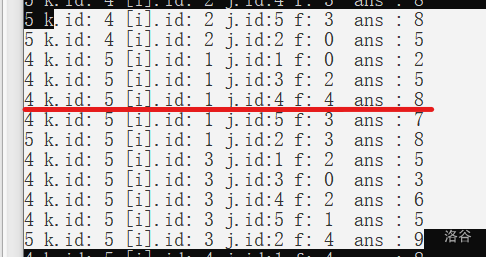
这里是找到了答案了

直接上代码吧，这道题三个for循环是可以写成传统Floyd的
但是无所谓的 反正要更新的点不会因为顺序乱了几下，就不更新，边权又不会变

但是转折点必须写排完序的那个e数组，即我们理解的k然后就是判断重边，对角线为0这些小问题了，然后没啥了，这题就这样了

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
struct node{
	int id,power;
}e[255];
int n,m,q;
int a,b,c;
int f[255][255];
int ans[255][255];
inline int read()
{
	int s=0;
	int w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-')w*=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		s=s*10+ch-'0';
		ch=getchar();
	}
	return s*w;	
}
bool cmp(node a,node b)
{
	return a.power<b.power;
}
int main()
{
	memset(f,0x3f,sizeof f);
		memset(ans,0x3f,sizeof ans);
	n=read(),m=read(),q=read();
	for(int i=1;i<=n;i++)
	{
		e[i].power=read();
		e[i].id=i;
	}
	sort(e+1,e+1+n,cmp);
	for(int i=1;i<=n;i++)
	{
		f[i][i]=0;
	}
	for(int i=1;i<=m;i++)
	{
		a=read(),b=read(),c=read();
       f[a][b]=f[b][a]=min(f[a][b],c);
		//重边	
	}
	for(int k=1;k<=n;k++)
	{
		for (int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
			
				f[e[i].id][e[j].id]=min(f[e[i].id][e[j].id],f[e[i].id][e[k].id]+f[e[k].id][e[j].id]);
				ans[e[i].id][e[j].id]=min(ans[e[i].id][e[j].id],f[e[i].id][e[j].id]+max(e[i].power,max(e[k].power,e[j].power)));
				//cout<<max(e[i].power,max(e[k].power,e[j].power))<<" k.id: "<<e[k].id<<" [i].id: "<<e[i].id<<" j.id:"<<e[j].id;
			//	cout<<" f: "<<f[e[i].id][e[j].id]<<"  ans : "<<ans[e[i].id][e[j].id]<<endl;
			}	
		}//比如1  -4 的过程 1-3-4 如果1-3 f数组并不会追踪路径 中走的 1-2-3    2>4>3>1
		//会造成点权出现问题  所以要排序  保证点权比较没有差错  
		//我可能走1 -2 - 4 也可以 1 - 3-4 那中间的路径的点的点权没法分析的 所以必须排序 确保 从小到大的走   毕竟只保存了最短路
	}//这里可能有个小疑问就是 我能不能继续从f【i】【j】一样 像原始flyod
	//一样 明显可以 上面代码以k为桥 所有点都会更新 只是题解不想这么麻烦吧 
	while(q--)
	{
		int st,fin;
		st=read(),fin=read();
		cout<<ans[st][fin]<<endl;
	}
	
	
	
	
	
	
	
	
	return 0;
}